P1852 跳跳棋 [LCA思想+二分答案]

题目描述

跳跳棋是在一条数轴上进行的。棋子只能摆在整点上。每个点不能摆超过一个棋子。



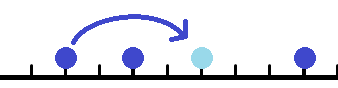
我们用跳跳棋来做一个简单的游戏：棋盘上有\(3\)颗棋子，分别在\(a,b,c\)这三个位置。我们要通过最少的跳动把他们的位置移动成\(x,y,z\)。（棋子是没有区别的）

跳动的规则很简单，任意选一颗棋子，对一颗中轴棋子跳动。跳动后两颗棋子距离不变。一次只允许跳过\(1\)颗棋子。

写一个程序，首先判断是否可以完成任务。如果可以，输出最少需要的跳动次数。

输入格式

第一行包含三个整数，表示当前棋子的位置\(a\ b\ c\)。（互不相同）

第二行包含三个整数，表示目标位置\(x\ y\ z\)。（互不相同）

输出格式

如果无解，输出一行\(NO\)。

如果可以到达，第一行输出\(YES\)，第二行输出最少步数。

输入输出样例

输入

1 2 3

0 3 5

输出

YES

2

说明/提示

\(20\%\) 输入整数的绝对值均不超过\(10\)

\(40\%\) 输入整数的绝对值均不超过\(10000\)

\(100\%\) 绝对值不超过\(10^9\)

分析

搜标签\(LCA\)搜到的这个题，挺侥幸的。

分析一下，一个三元组，由于每次只能越过一个棋子跳，所以在有序的状态下只有三种可能：

\(1\)、从中间向两边跳。 \(2\)、从左向中间跳，条件是左边的距离小于右边。 \(3\)、从右向中间，条件与上边相反。

根据这个我们可以看出来一个性质：棋子位置的状态可以近似看作一个二叉树，而它的根节点就是左右两边距离相等的情况，也就是只能从中间向两边跳，那么这个问题的第一问就很好解决了，因为假如两个三元组跳到所谓的根的状态的时候的位置不一样，那么肯定从一个不能扩展到另一个，这时候只需要让两个三元组表示的坐标一直跳，直到跳不了了，那么就到了根，判断一下根是否相同，不相同就是\(NO\)，否则继续向下找需要跳多少步。

第一个问题解决了，接下来解决第二个：

想一下，如果两个状态在同一个二叉树里，而且我们需要求他们之间跳多少步才能相等。！！！！这不就显然了吗，树上距离当然要用\(LCA\)了。可是这个三元组的状态是没法建树的，所以我们只需要用到求\(LCA\)的思想就行了，即：先把两个状态距离根的步数统一（对应到求\(LCA\)里就是把深度调到一样），然后二分向上跳的步数，最后找到一个两个状态都向上跳\(L\)步，那么总的步数就是之前的高度（步数差）加上二分出来的答案的二倍！！成功切掉。

代码

#include<bits/stdc++.h>
using namespace std;
const int maxn = 5;
const int Inf = 1e9+10;
int a[maxn],b[maxn];
struct Node{//结构体存状态
	int a[maxn];
};
int ans,jl;
int dep1,dep2;
Node js(int *a,int dep){
	int d1 = a[2] - a[1];
	int d2 = a[3] - a[2];
	Node ans;
	for(int i=1;i<=3;++i){//记录状态
		ans.a[i] = a[i];
	}
	if(d1 == d2)return ans;//如果不能继续跳，那么就是根，直接返回
	if(d1 < d2){//左边距离中间小于右边，那么就向右边跳
		int step = min(dep,(d2-1)/d1);//找到这个状态能跳多少步
		dep -= step;//总的步数减去这个状态走的步数
		jl += step;//jl记录的是一共走了多少步
		ans.a[2] += step * d1;//更新位置
		ans.a[1] += step * d1;
	}
	else{//左边距离中间大于右边，那么就向左边跳，下边都是一样的，就是更新位置需要减，也就是向左更新
		int step = min(dep,(d1-1)/d2);
		dep -= step;
		jl += step;
		ans.a[2] -= step * d2;
		ans.a[3] -= step * d2;
	}
	if(dep)return js(ans.a,dep);//如果还能跳就继续跳
	else return ans;不能就返回
}
int main(){
	for(int i=1;i<4;++i){
		scanf("%d",&a[i]);
	}
	for(int i=1;i<4;++i){
		scanf("%d",&b[i]);
	}
	sort(a+1,a+4);
	sort(b+1,b+4);
	Node zt1 = js(a,Inf);//找到第一个三元组的根
	dep1 = jl;
	jl = 0;
	Node zt2 = js(b,Inf);//第二个三元组的根
	dep2 = jl;
	jl = 0;
	int flag = 0;
	for(int i=1;i<4;++i){
		if(zt1.a[i] != zt2.a[i])flag = 1;
	}
	if(flag){//如果根状态不一样，直接输出NO
		puts("NO");
		return 0;
	}
	if(dep1 > dep2){
		swap(dep1,dep2);
		for(int i=1;i<4;++i){
			swap(a[i],b[i]);
		}
	}
	int l = 0, r = dep1;
	ans = dep2 - dep1;//记录深度差
	zt1 = js(b,ans);//调整到同一深度
	for(int i=1;i<4;++i){//记录下来状态
		b[i] = zt1.a[i];
	}
	while(l <= r){//二分答案
		int mid = (l+r)>>1;
		flag = 0;
		zt1 = js(a,mid);
		zt2 = js(b,mid);
		for(int i=1;i<4;++i){
			if(zt1.a[i] != zt2.a[i])flag = 1;
		}
		if(flag)l = mid+1;
		else r = mid-1;
	}
	puts("YES");
	printf("%d\n",ans+2*l);
	return 0;
}