题解 洛谷P1990 覆盖墙壁

DP康复训练题

原题：洛谷P1990

核心：递推/DP

题源应该是铺地砖，所以采用一摸一样的思路，只是有两种不同的方块

我们先用最最简单的方式尝试一下枚举当最后一行被填满的情况：

1.如果我们只用第一种长方形的方块让最后一行填满，那就只有两种情况：

　　A.最后一列刚好是一个竖着的砖头：　　　　　B.最后两列都是横着的砖头：

　　　　　　　　　　　　　

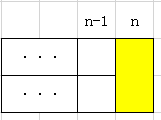
　　那这个时候我们先定义一个数组F，F的意思取fill，F[i]表示刚好把第i列填满时有多少种方法。

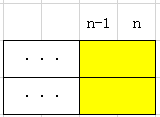
　　这样的话，因为我们现在只用了第一种方块，所以只可以得出一部分递推公式：F[x]=F[x-1]+F[x-2]+······。这个省略号里的内容就应该是考虑第二种方块时候产生的总数。

2.那我们接着来考虑第二种方块填满最后一行时的情况：

　　表面上看有两种：

　　　　　

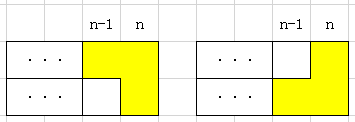
　　实际上这两个是一模一样的，他们只不过是取决于第n-1列那多出来的那一半是在哪里。所以，如果要使用第二种，最核心的问题是会出现一列有一半的情况。所以我们试着来表示一下这种只有一半的情况：

　　再定义一个数组H，H的意思取half,H[i]表示把第i列填上一半有多少种方法。

　　我们再来想一想怎么样才能让这一行出现一半：一共有四种情况:

　　A.在一个填满的列后面加上一个第二种方块：   B.在一个一半的列的空位上放一个横着的第一种方块：

　　　　 　　　　　　　　

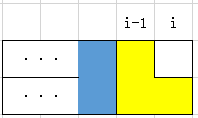
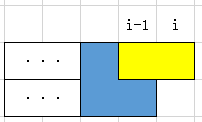
　　以及他们上下对称的另外两种情况。对B情况，为什么非要加在空位上呢？那如果加在凸起来的那一块上：

　　　　　

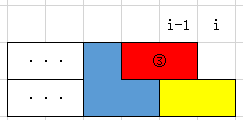
　　我们最后需要的是每一列都被填满的情况，所以说上面的空位迟早要填，填的话又只能填第一种方块，所以如果在凸起来的那一块加的话是等效于先在③位置上先放一个，再往新形成的空位上再加上一个第一种方块，是属于按照情况B放之后出现的下一列的一种情况。所以说，H数组的真正完整的理解应该是：在第i-1列填满的情况下，让第i列只有一半有多少种方法。

　　回到正题，接着来推H的递推式：

　　情况A:取决于第i-1列有多少种填满的方式，而且凸出的那一块是可以在上也可以在下两种方式，所以总的是F[i-1]*2

　　情况B:取决于第i-1列有多少种填一半的方式,但是当前这一块放的位置实际上取决于i-1列的空位在哪里，所以这种情况下是和上一个半行一一对应的，就是H[i-1]

　　合起来：H[i]=F[i-1]*2+H[i-1]

　　那么要怎么样把一个填了一半的在下一列变成一个完整的呢？(也就是从H[i]变到F[i+1])

　　更简单，往空格那里塞一个第二种方块不就好了：

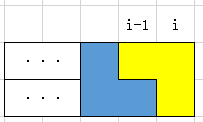　　 　　这个图像好像有一点点眼熟？（x

　　这样的话，在F[i]的推导式里空缺的一项就出来了：H[i-1]

那么把所有情况总结起来，得出最后的状态转移方程：

　　F[i]=F[i-1]+F[i-2]+H[i-1]

　　H[i]=F[i-2]*2+H[i-1]

还差一个初状态，画画图可以发现：

　　F[1]=1(就竖着放一个)，F[2]=2(横着放两个，竖着放两个)

　　H[1]=0(随便怎么放第二个方块的凸块只能在第二列)，H[2]=2（凸口在上\在下）

好了，结束。

AC代码：（就懒得打注释了）

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int F[10000010]={0},H[1000010]={0};
int n;
int _r(){
    int x=0;
    char c=getchar();
    while(c>'9'||c<'0')c=getchar();
    while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();
    return x;
}
void DP(){
    F[1]=1;
    F[2]=2;
    H[2]=2;
    for(int i=3;i<=n;i++){
        F[i]=F[i-1]+F[i-2]+H[i-1];
        H[i]=2*F[i-2]+H[i-1];
        F[i]%=10000;
        H[i]%=10000;
    }
}
int main(){
    n=_r();
    DP();
    printf("%d",F[n]);
    return 0;
}