Java数据结构（十四）—— 平衡二叉树（AVL树）

平衡二叉树（AVL树）

二叉排序树问题分析

1. 左子树全部为空，从形式上看更像一个单链表

2. 插入速度没有影响

3. 查询速度明显降低

4. 解决方案：平衡二叉树

基本介绍

1. 平衡二叉树也叫二叉搜索树，保证查询效率较高

2. 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两棵子树都是一棵平衡二叉树

3. 常用的实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等

平衡二叉树左旋转

使用条件

右子树高度与左子树高度插值大于1的时候，使用左旋转

要求

给定数列{4，3，6，5，7，8}，创建对应的平衡二叉树

创建二叉排序树

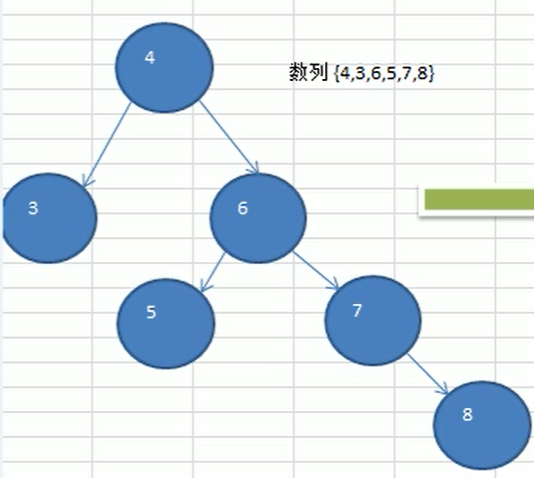
此时若转换为平衡二叉树，降低右子树的高度

思路分析

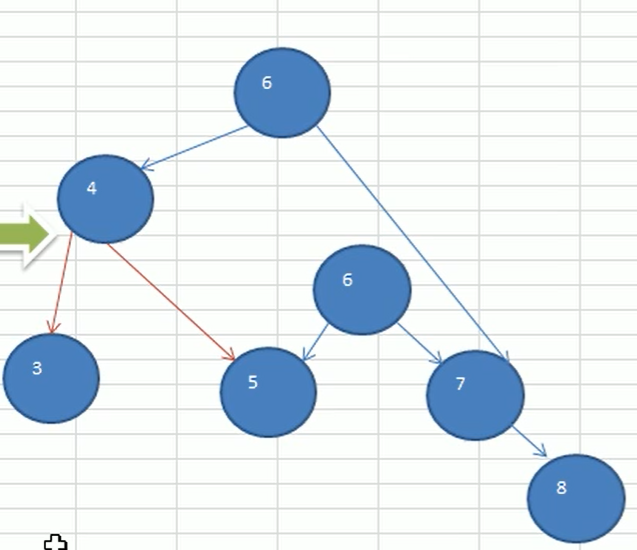
1. 创建一个新节点newNode ，值等于当前根节点的值

2. 把新节点的左子树设置为当前节点的左子树，newnode.left = left

3. 把新结点的右子树设置为当前节点右子树的左子树newNode.right = right.left

4. 把当前节点的值换位右子节点的值 value = right.value

5. 把当前节点的右子树设置成右子树的右子树right = right.right

6. 把当前节点的左子树设置为新节点 left = newLeft

转换后

平衡二叉树右旋转

要求

使用数列{10，12，8，9，7，6}，创建平衡二叉树

创建二叉排序树

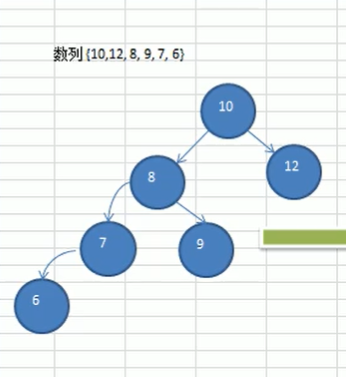
基本思路

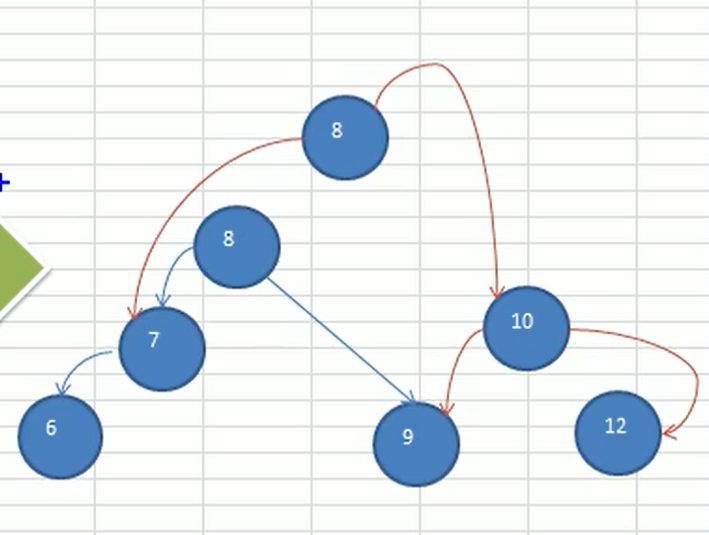
1. 创建新的节点newNode，使得newNode.value = this.value

2. 将newNode的右子树设置为this的右子树,newNode.right = this.right

3. 将newNode的左子树设置为this左子树的右子树，newNode.left = this.left.right

4. 把this节点的值换为左子节点的值，this.value = this.left.value

5. 将this节点的左子树设置为左子树的左子树，this.left = this.left.left

6. 将this节点的右子树 设置为newNode，this.right = newNode

转换后

平衡二叉树双旋转

要求

使用数列{10，11，7，6，8，9}，创建平衡二叉树

创建二叉排序树

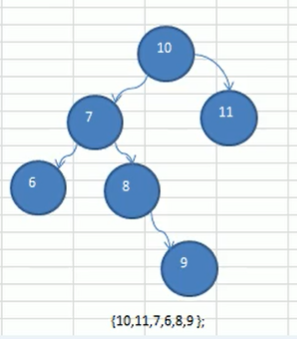
思路分析

• 当孩子节点满足左旋转或右旋转条件时，先平衡孩子 节点，后平衡父节点

创建平衡二叉树代码实现

package com.why.tree;
​
/**
 * @Description TODO 平衡二叉树
 * @Author why
 * @Date 2020/12/6 15:56
 * Version 1.0
 **/
public class AVLTreeDemo {
    public static void main(String[] args) {
        int[] arr = {10,11,7,6,8,9};
        //创建AVLTree对象
        AVLTree avlTree = new AVLTree();
​
        //添加节点
        for (int i = 0; i < arr.length; i++) {
            avlTree.add(new AVLNode(arr[i]));
        }
​
        //遍历
        System.out.println("中序遍历:");
        avlTree.midOrder();
​
        //根节点树的高度
        System.out.println("根节点树的高度: " + avlTree.height());
        System.out.println("左子树高度：" + avlTree.leftHeight());
        System.out.println("右子树高度：" + avlTree.rightHeight());
        System.out.println("根节点：" + avlTree.getRoot());
​
    }
}
​
/**
 * AVL,平衡二叉树
 */
class AVLTree{
    private AVLNode root;
​
    public AVLNode getRoot() {
        return root;
    }
​
    public void setRoot(AVLNode root) {
        this.root = root;
    }
​
    /**
     * 添加节点
     * @param node
     */
    public void add(AVLNode node){
        if (root == null){//直接放上
            root = node;
        }else {
            root.add(node);
        }
    }
​
    /**
     * 中序遍历
     */
    public void midOrder(){
        if (root != null){
            root.midOrder();
        }else {
            System.out.println("二叉排序树为空");
        }
    }
​
    /**
     * 查找需删除的节点
     * @param value
     * @return
     */
    public AVLNode search(int value){
        if (root == null){
            return null;
        }else {
            return root.search(value);
        }
    }
​
    /**
     * 查找父节点
     * @param value
     * @return
     */
    public AVLNode searchParent(int value){
        if (root == null){
            return null;
        }else {
            return root.searchParent(value);
        }
    }
​
    public void deleteNode(int value){
        if (root == null){
            return;
        }else {
            //找到需删除的节点
            AVLNode targetNode = search(value);
            if (targetNode == null){//未找到
                return;
            }
            //如果二叉排序树只有一个节点
            if (root.left == null && root.right == null){
                return;
            }
​
            //查找需删除的节点的父节点
            AVLNode parent = searchParent(value);
            if (targetNode.left == null && targetNode.right == null){//删除的节点是叶子节点
                //判断targetNode是父节点的左子节点还是右子节点
                if (parent.left != null && parent.left.value == value){//是左子节点
                    parent.left = null;
                }else if (parent.right != null && parent.right.value == value){//是右子节点
                    parent.right = null;
                }
            }else if ((targetNode.left != null && targetNode.right == null) ||
                    (targetNode.right != null && targetNode.left == null)) {//只有一棵子树
                //确定targetNode的节点是左节点还是右节点
                if (targetNode.left != null) {//左子节点
                    if (parent != null){//非根节点
                        //确定targetNode是parent的左子节点还是右子节点
                        if (parent.left.value == value) {//左子节点
                            parent.left = targetNode.left;
                        } else {//右子节点
                            parent.right = targetNode.left;
                        }
                    }else {
                        root = targetNode.left;
                    }
                } else {//右子节点
                    if (parent != null){
                        //确定targetNode是parent的左子节点还是右子节点
                        if (parent.left.value == value) {//左子节点
                            parent.left = targetNode.right;
                        } else {//右子节点
                            parent.right = targetNode.right;
                        }
                    }else {
                        root = targetNode.right;
                    }
                }
            }else {//删除的节点有两颗子树
                //找到最小值并删除
                int minValue = deleteRightMin(targetNode.right);
                //将最小值赋值给targetNode.value
                targetNode.value = minValue;
            }
        }
    }
​
    /**
     * 寻找最小值
     * @param node
     * @return
     */
    public int deleteRightMin(AVLNode node){
        AVLNode target = node;
        while (target.left != null){
            target = target.left;
        }
        //这时target指向最小节点
        //删除最小节点
        deleteNode(target.value);
        //返回最小节点的value
        return target.value;
    }
​
    /**
     * 返回根节点树的高度
     * @return
     */
    public int height(){
        return root.height();
    }
​
    /**
     * 左子树的高度
     * @return
     */
    public int leftHeight(){
        return root.leftHeight();
    }
​
    /**
     * 右子树的高度
     * @return
     */
    public int rightHeight(){
        return root.rightHeight();
    }
​
}
​
/**
* 节点类
*/
class AVLNode{
    int value;
    AVLNode left;
    AVLNode right;
​
    public AVLNode(int value) {
        this.value = value;
    }
​
    /**
     * 添加节点，递归形式，需满足二叉排序树的要求
     * @param node
     */
    public void add(AVLNode node){
        if (node == null){
            return;
        }
        //判断传入的节点的值和当前子树的根节点的值的关系
        if (node.value < this.value){
            if (this.left == null){//当前节点左子节点为空
                this.left = node;
            }else {//不为空，递归向左子树添加
                this.left.add(node);
            }
        }else {
            if (this.right == null){
                this.right = node;
            }else {
                this.right.add(node);
            }
        }
​
        //当添加完节点后，若右子树的高度比左子树的高度的数值大于1
        if (rightHeight() - leftHeight() > 1){
            if (right != null && right.leftHeight() > right.rightHeight()){
                //对右子树 右旋转
                right.rightRotate();
            }
            //左旋转
            this.leftRotate();
            return;
        }
        //当添加完节点后leftHeight - rightHeight > 1
        if (leftHeight() - rightHeight() > 1){
            if (left != null && left.rightHeight() > left.leftHeight()){
                //对左子树左旋转
                left.leftRotate();
            }
            //右旋转
            this.rightRotate();
            return;
        }
    }
​
    /**
     * 中序遍历
     */
    public void midOrder(){
        if (left != null){
            this.left.midOrder();
        }
        System.out.println(this);
        if (this.right != null){
            this.right.midOrder();
        }
    }
​
    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }
​
    /**
     * 寻找需要删除的节点
     * @param value
     * @return
     */
    public AVLNode search(int value){
        if (value == this.value){//找到
            return this;
        }else if (value < this.value){//向左子树查找
            if (this.left == null){
                return null;
            }
            return this.left.search(value);
        }else {//向右子树查找
            if (this.right == null){
                return null;
            }
            return this.right.search(value);
        }
    }
​
    /**
     * 查找需要删除节点的父节点
     * @param value
     * @return
     */
    public AVLNode searchParent(int value){
        if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)){
            //找到父节点返回当前节点
            return this;
        }else {
            //如果查找的值小于当前节点的值
            if (value < this.value && this.left != null){//左子树查找
                return this.left.searchParent(value);
            }else if (value >= this.value && this.right != null){//右子树查找
                return this.right.searchParent(value);
            }else {
                return null;//没有找到父节点
            }
        }
    }
​
    /**
     * 返回以当前节点为根节点的树的高度
     * @return
     */
    public int height(){
        return Math.max(this.left == null ? 0 : this.left.height(),this.right == null ? 0 : this.right.height()) + 1;
    }
​
    /**
     * 返回左子树的高度
     * @return
     */
    public int leftHeight(){
        if (left == null){
            return 0;
        }else {
            return left.height();
        }
    }
​
    /**
     * 返回右子树的高度
     * @return
     */
    public int rightHeight(){
        if (right == null){
            return 0;
        }else {
            return right.height();
        }
    }
​
    /**
     * 左旋转方法
     */
    private void leftRotate(){
        //创建新的节点，以当前根节点的值创建
        AVLNode newNode = new AVLNode(this.value);
        //把新的节点的左子树设置为当前节点的左子树
        newNode.left = this.left;
        //把新节点的右子树设置为当前节点右子树的左子树
        newNode.right = this.right.left;
        //将当前节点的值修改为右子树的值
        this.value = this.right.value;
        //将当前节点的右子树设置为右子树的右子树
        this.right = this.right.right;
        //将当前节点的左子节点设置为新的节点
        this.left = newNode;
    }
​
    /**
     * 右旋转
     */
    private void rightRotate(){
        //以当前节点的值创建新的节点
        AVLNode newNode = new AVLNode(this.value);
        //将新节点的右子树设置为当前节点的右子树
        newNode.right = this.right;
        //将当前节点的左子树设置为当前节点左子节点的右子树
        newNode.left = this.left.right;
        //将当前节点的值用左子节点的值替换
        this.value = this.left.value;
        //将当前节点的左子节点设置为当节点左子节点的左子树
        this.left = this.left.left;
        //将当前节点的右子节点设置为新节点
        this.right = newNode;
    }
}

所有源码都可在gitee仓库中下载：https://gitee.com/vvwhyyy/java_algorithm