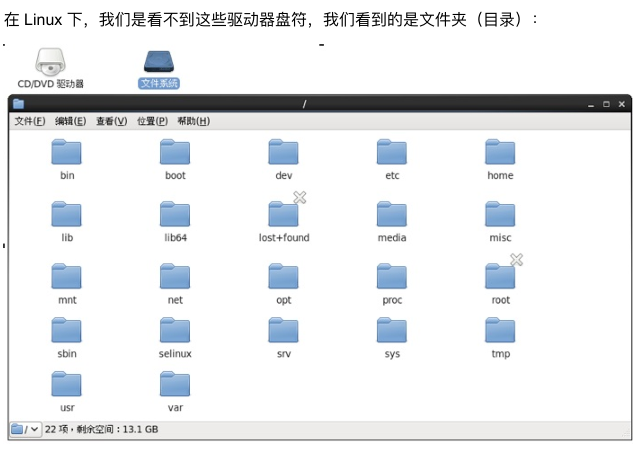
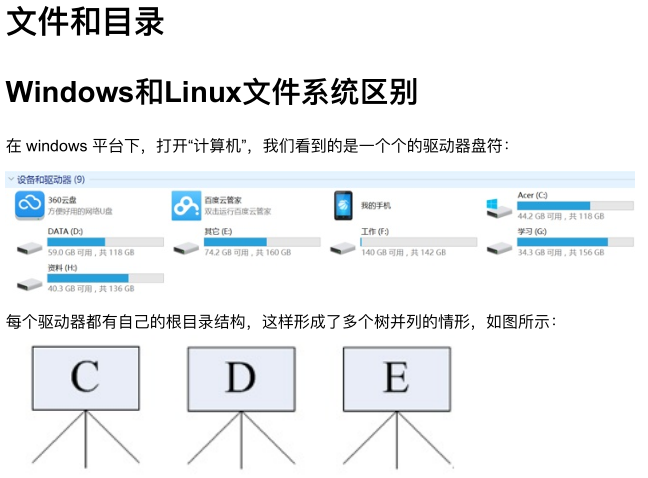
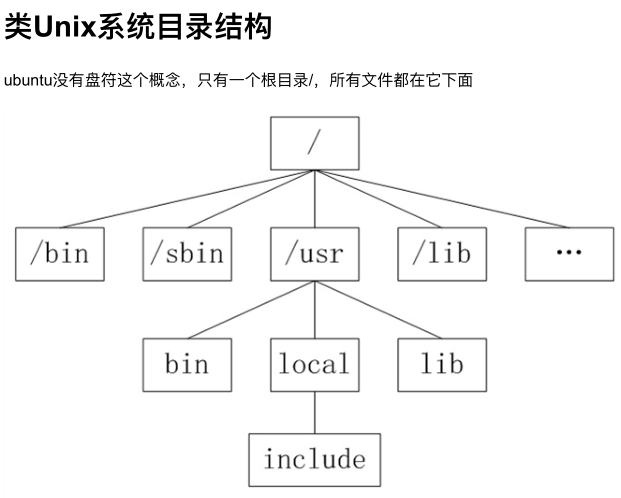
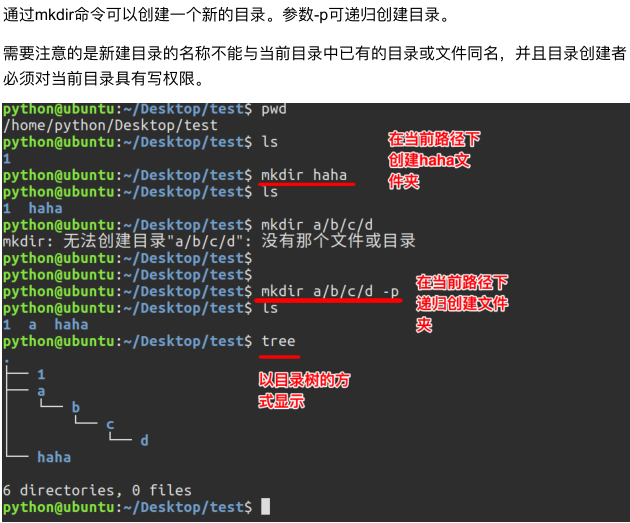
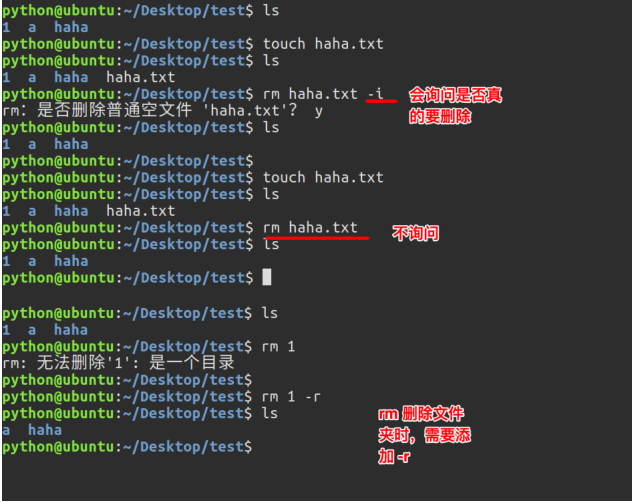
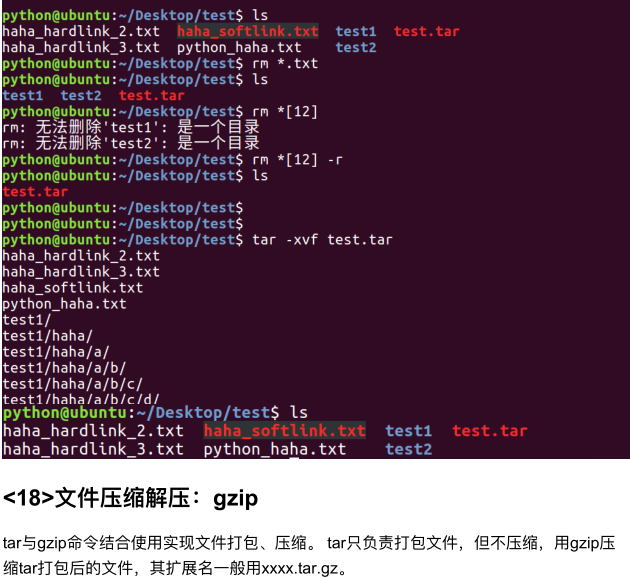
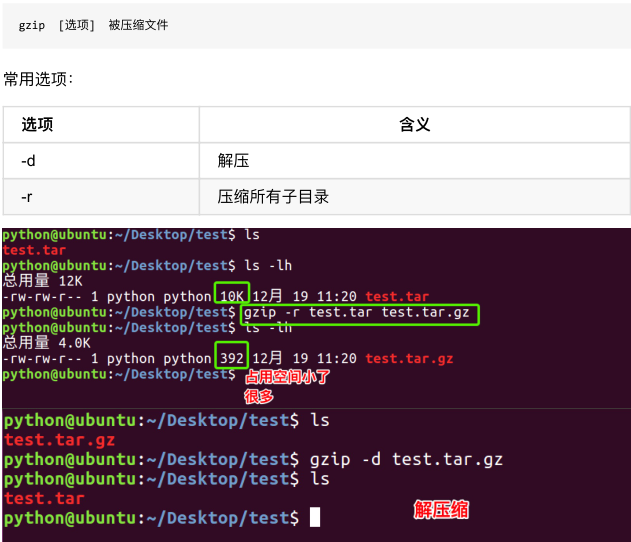
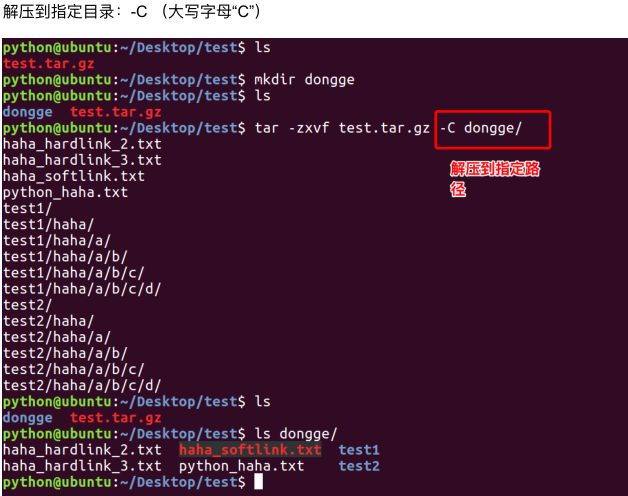
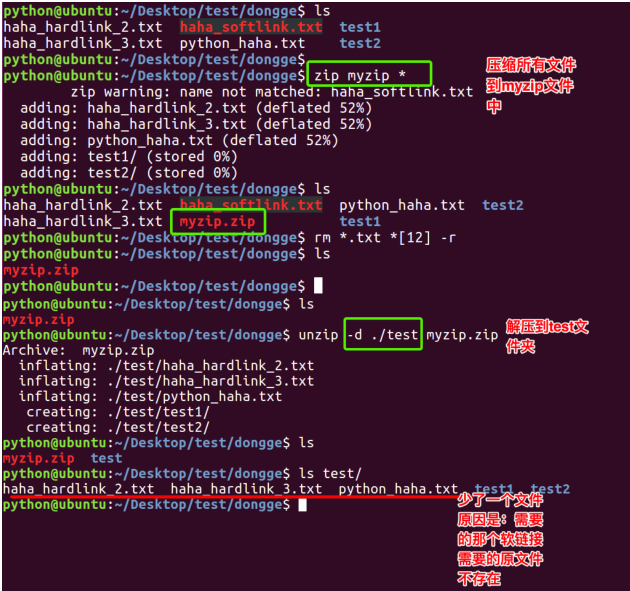
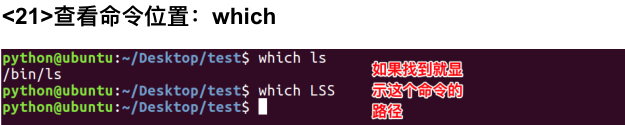
linux_1














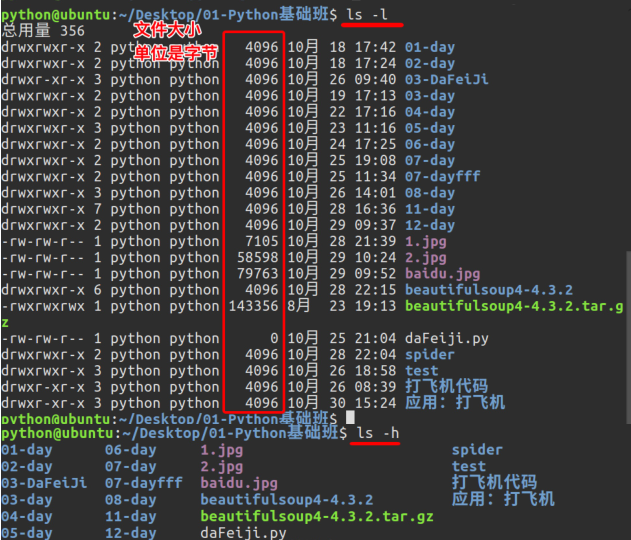
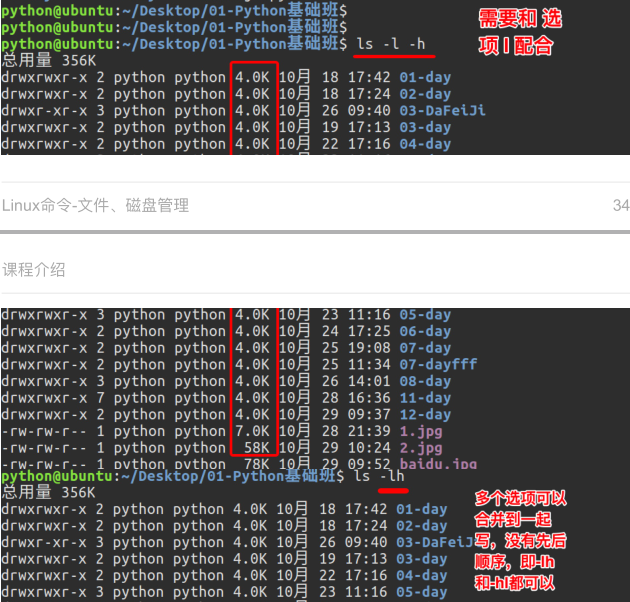
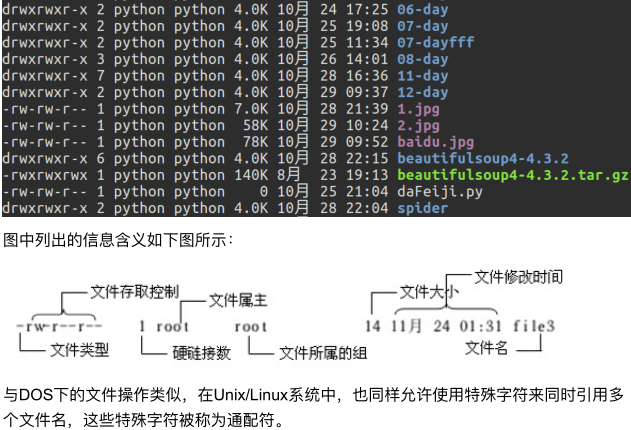
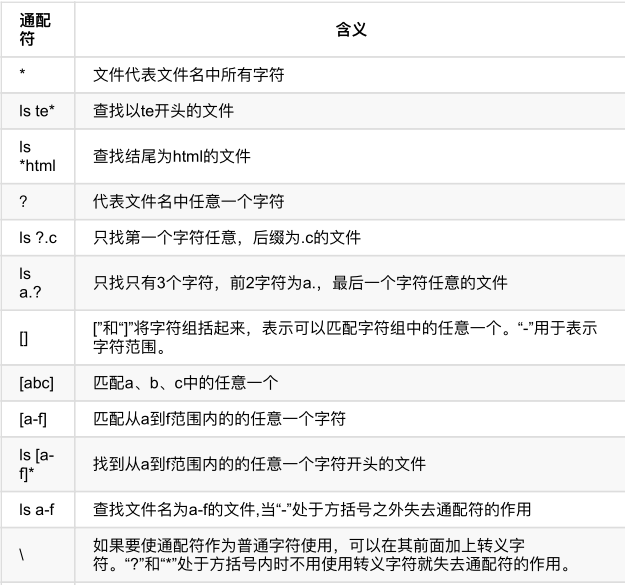






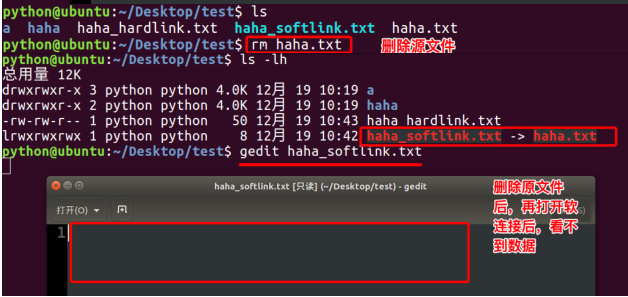
注:
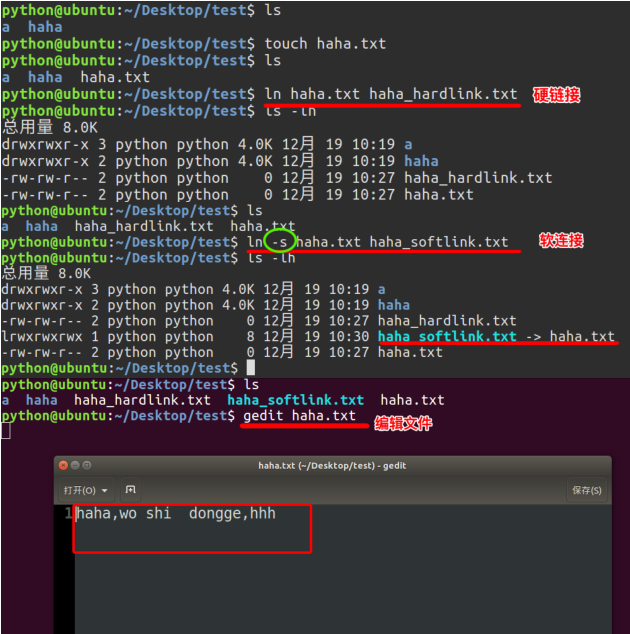
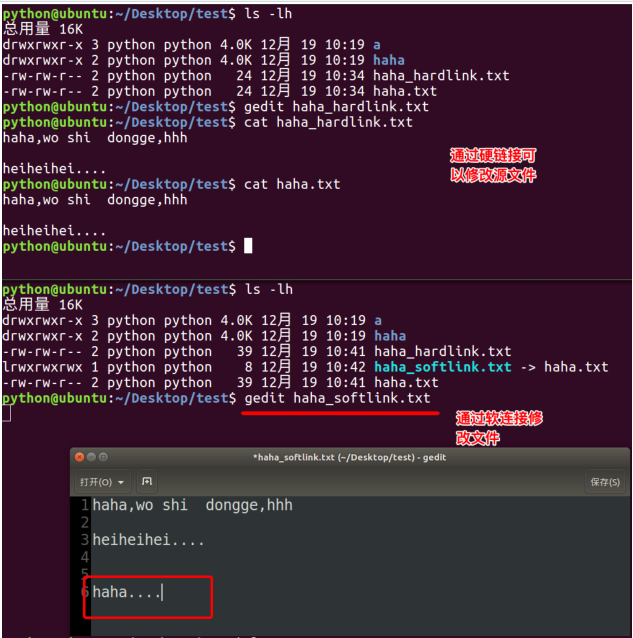
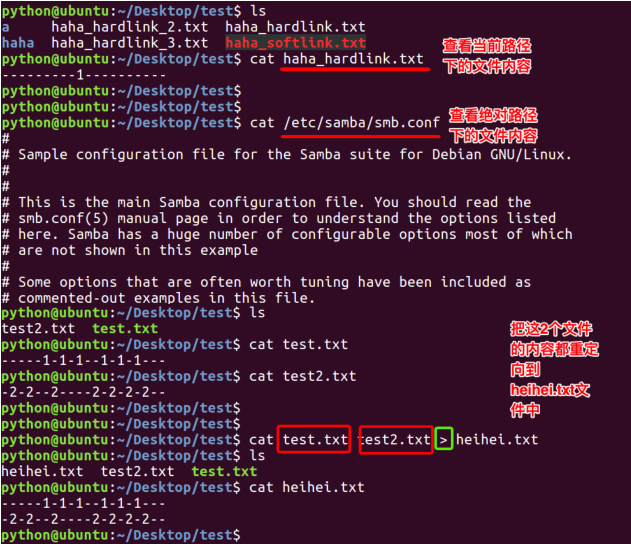
创建软连接:
"ln -s xxx 路径1" 在路径1创建xxx的软连接
特点:
1.文件类型 l
2.相当于windows的快捷方式
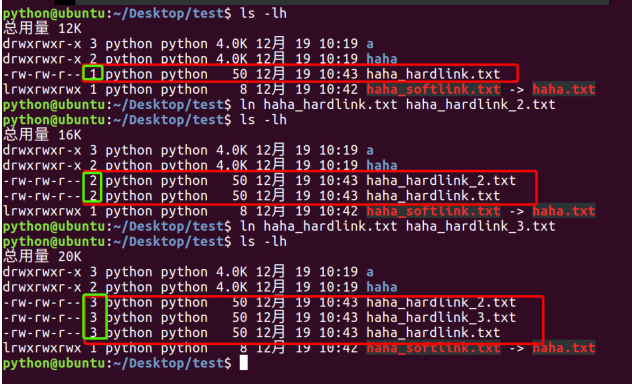
创建硬链接:
"ln xxx 路径1" 在路径1创建xxx的软连接
特点:
1.文件类型 -
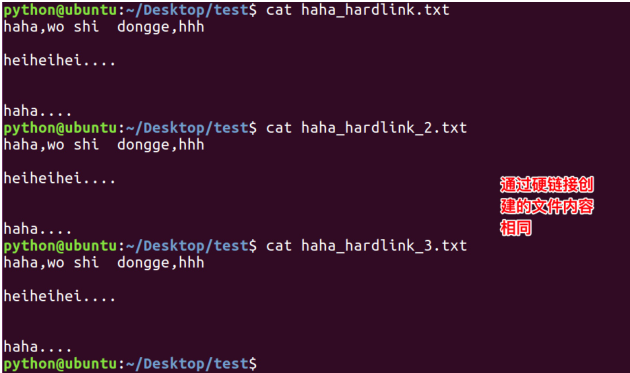
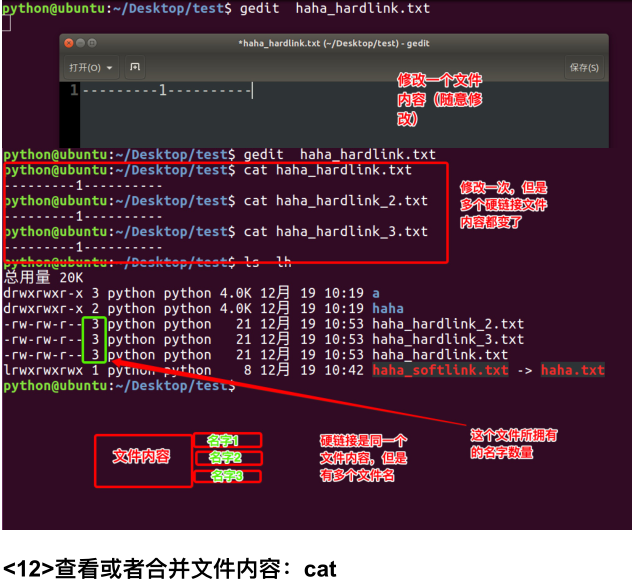
2.相当于拷贝,但是可以同步更新。也就是一个文件有多个文件名


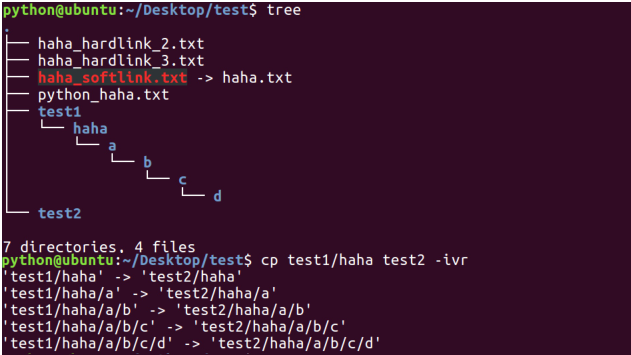


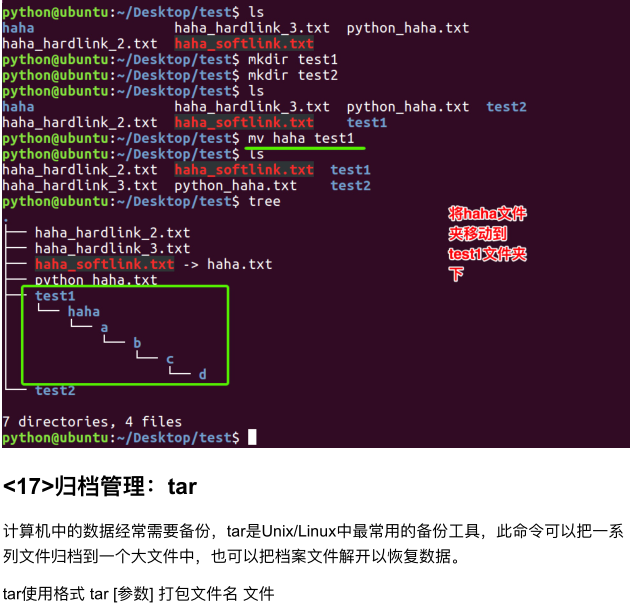
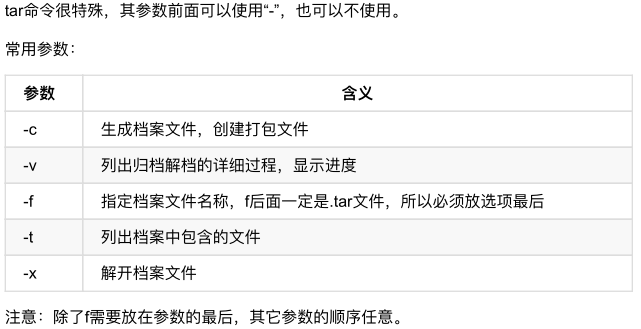
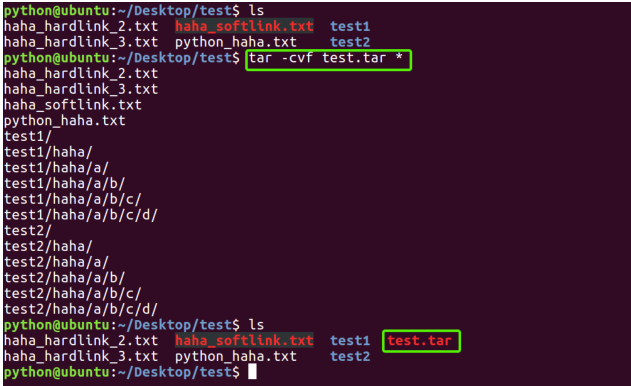




linux_1的更多相关文章
- Linux系统管理_主题01 :初识Linux_1.7 关闭和重启Linux_shutdown
shutdown [选项] 时间 [警告消息] 系统关机 -c 取消前一个 shutdown 命令.值得注意的是,当执行一个如 “shutdown -h 11:10”的命令时,只要按“Ctrl+C ...
- Linux系统管理_主题01 :初识Linux_1.6 用好帮助文档man
在 man 界面中,可以使用如下快捷键来进行操作: 上/下箭头 向上/下滚动一行 [Space] 向下翻一页 [Page Down] 向下翻一页 [Page Up] 向上翻一页 [ ...
- Linux系统管理_主题01 :初识Linux_1.5 与Linux进行交互_echo_nano_Tab_whoami
[root@izkfv3zmvcl0omz ~]# 其中,'root'为登录用户名,'izkfv3zmvcl0omz'为登录主机名,’~’ 表示当前用户正处在 root 用户的 家目录中,’#’则表示 ...
- 2016第七季极客大挑战Writeup
第一次接触CTF,只会做杂项和一点点Web题--因为时间比较仓促,写的比较简略.以后再写下工具使用什么的. 纯新手,啥都不会.处于瑟瑟发抖的状态. 一.MISC 1.签到题 直接填入题目所给的SYC{ ...
- python学习-day14:集合,函数,格式化
一.集合 定义:由不同元素组成的集合.集合是一组无序排列的可hash值, 可以作为字典的key.元素必须是不可变类型:只能存放数字,字符串,字典 特性:集合的目的是将不同的值放在一起,不同的集合之间可 ...
- ubuntu14.04 64位 安装eclipse
ubuntu14.04 64位 安装eclipse 1 在官网上下载eclipse http://www.eclipse.org/downloads/下载eclipse-jee-luna-SR1-li ...
- python基础语法三
集合: 1.不同元素组成 2.无序 3.集合中的元素必须是不可变类型 s = {1, 2, 3 } #定义集合 s = set('hello') print(s) s.pop() #指定删除 s.r ...
- day14 Python集合的补充
python_1 = ['charon','pluto','ran','charon'] linux_1 = ['ran','xuexue','ting'] p_s = set(python_1) l ...
- day14 Python集合关系运算交,差,并集
low逼写法,没用集合 python_1 = ['charon','pluto','ran'] linux_1 = ['ran','xuexue','ting'] python_and_linux = ...
随机推荐
- E20190402-hm
porxy n. 代理服务器; 代表权; 代理人,代替物; 委托书; enroll v. 招收; 注册; 登记; 加入; enrollment n. 注册; 登记; 入会;
- E20190225-hm
seal n. 密封; 印章; 海豹; 封条; v. 密封; 盖章; 决定; 封上(信封); primitive adj. 原始的; 发展水平低的; 落后的; [生物学] 原生的; n. 原始 ...
- 删除链表中的倒数第n个元素
示例: 输入链表:1->2->3->4->5 , 2 输出:1->2->3->5 Python解决方案1: # Definition for singly-l ...
- 1107 Social Clusters (30 分)
When register on a social network, you are always asked to specify your hobbies in order to find som ...
- Codeforces698B【并查集+拆环】
好题,好题,第一次写这个神秘的拆环.. 题意: 给你n个数,第i个数代表点i连向点a[i], 将这副图变成树,求最小改变边的数量: 思路: 已知有向树的定义, 除了根节点外每个节点都有且仅有一条边都指 ...
- 小程序地区时间自定义选择器 picker
进入微信公众平台小程序开发文档搜索 picker 点进去后下滑,点击在开发者工具中预览即可
- 洛谷P4884 多少个1?(BSGS)
传送门 模数好大……__int128好麻烦……而且BSGS第一次写有点写蒙了…… $11...1(N个1)\equiv k(mod m)$很难算,那么考虑转化一下 先把$11...1(N个1)$写成$ ...
- native-echarts 在安卓上无法显示出来
1.native-echarts 的配置是百度echarts 2.模拟器上试了很多次都显示不出来(具体不清楚,我的是这样) 3.真机测试可以显示图表,以下是配置: a.将node_modules\na ...
- JavaScript 对象的原型扩展(JS面向对象中的继承)
<script type="text/javascript"> function person(name, age) { this._name = name; this ...
- SOA思想
参考:https://www.cnblogs.com/renzhitian/p/6853289.html 是什么 SOA service-oriented architecture 面向服务的体系结构 ...
