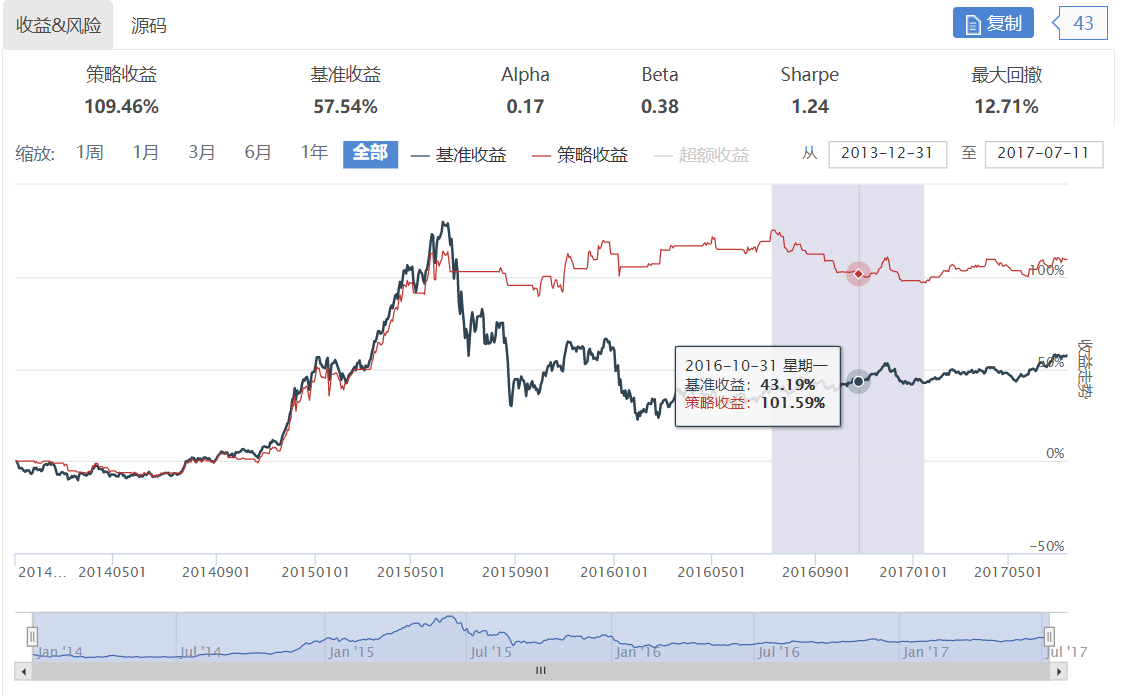
基于KMeans的指数择时策略

　【导语】：聚类分析是指将物理或者抽象对象的结合分组为由类似对象组成的多个类的分析过程。简单来讲，聚类就是通过一些特征去自动识别一个大群体中的多个子群体，这些子群体中的对象彼此之间相似度高，而子群体之间差异较大。聚类的概念其实是Machine Learning中的一个子分支，在很多情况下，我们无法直接获得足够的带标签（分类）的数据样本来训练我们的模型，在这种情况下，聚类分析就显得尤为重要。它能够在给定的无标签样本中根据其特征给每个样本分类。

　　【策略思想】

　　这里有必要简单介绍一下KMeans。KMeans是聚类分析中的一种算法。它的算法过程大致是这样的：

　　有一天，你想要给5只西瓜分类，你已经测量好了这些西瓜的质量、半径、颜色深度等一系列特征，你是一个挑西瓜的小白，并不懂得好瓜应该长成什么样。这个时候，你想通过Kmeans聚类算法来对这些瓜分类。

　　1.你的目标是区分好瓜和坏瓜，所以你给定了想要聚类的数量为2。

　　2.你随机挑选了2只瓜作为好瓜和坏瓜的起点，当然了，其实你并不知道它们是不是真的是好瓜和坏瓜，有可能给的定义完全是相反的。（那么我们暂定1号瓜作为好瓜，2号瓜作为坏瓜）

　　3.这个时候你顺理成章的想，既然现在假设好了好瓜和坏瓜，那么现在第3只瓜的各个特征跟哪只瓜更加相似就应该划分都哪只瓜里去。所以你分别计算了每只瓜和1号瓜以及2号瓜的“距离”大小，发现3、4号瓜与1号更加相似，5号瓜与2号更加相似。于是得到了下面的结果。 
　　

　　4.一只瓜的分类未必是准确的，而前面你直接指定了1号和2号瓜的命运。。所以，你现在需要更新好瓜和坏瓜的标准，说专业点就叫做更新聚类中心。怎么做呢？对于第1类来说，你计算了1、3、4这几只瓜各个特征的平均值，重新生成了一个聚类中心；类似的，对于第2类来说，计算了2、5号瓜各个特征的平均值。

　　5.经过第4步，已经完成了一次聚类中心的更新。那么由于好瓜和坏瓜的定义被改变了（不再是1号或者2号瓜中的任何一个），所以需要重新更新每只瓜的归属，于是你重复上面第3步，重新将每只瓜根据与更新后的聚类中心的距离分类到两个类中。

　　6.这个时候为了保证一定的科学性，你需要多重复几次上面的过程，直到最后两个类别的聚类中心都基本不改变或者达到了指定的迭代次数。算法就停止了。

　　这也是K-Means算法名称的来源，K代表了给定的聚类数量，也就是上面的2，Means则代表了对于这个算法而言，它的聚类中心是通过计算样本点的均值而来的。

　　进入正题。。

　　那么思路就来了，我们可以给定一些特征来描述指数的任意一天，比如过去14天的平均波动率，过去30天的平均成交量，等等等等。然后在给定的历史数据区间上（训练集，如2005-01-01至2013-12-31）对训练样本进行训练，比如目标是为了预测某一天是涨是跌，我们可以像刚才吃瓜的例子一样，给K-Means算法参数K=2。

　　刚才西瓜的例子中的特征向量：

　　[质量, 半径, 颜色深度, ...] ………………一只瓜

　　现在的特征向量：

　　[14日ATR, MACD, 30日avg_volume, ...] ………………一个交易日

　　换句话说，现在的任何一个交易日就对应了一只瓜。

　　得到了特征向量以后，按照上面的KMeans算法步骤，就可以得到每个交易日被分到哪个类中的结果了。比如我们以5个交易日举例。

　　

　　要注意，到现在为止，我们还不知道类1和类2的具体含义是什么。所以我们需要在数据集上进行验证。这里我们也给出这5个交易日的涨跌情况。于是，我们可以计算出这两个类别在训练集上的累积收益情况：

　　类1：0.9994×0.9967 = 0.9961 （-0.39%）

　　类2：1.0047×1.0077×1.0044 = 1.0169 （ 1.69%）

　　我们发现，在这里，我们的模型表现非常棒，明确的将所有上涨和下跌的交易日分到了两类里，类1和类2的意义也相当明确，1代表弱势，2代表涨势。

　　所以，我们可以使用这个模型进行择时判断，如果预测后一天是涨势，那么就在第二天开盘开仓，如果预测后一天为弱势，那么就在第二天开盘卖出清仓。

　　【注意点】

　　1.标准化。KMeans是基于欧式距离计算样本点之间的距离，所以务必在训练模型之前进行特征的标准化，否则会在计算距离时严重偏向值较大的属性特征，相当于自带了不同的权重。使用Min-Max或者Z-score标准化都可。

　　2.特征的挑选和个数。由于KMeans的迭代过程都利用了样本点之间的距离，距离的计算又都是由特征而来的，所以选取好的特征以及合适数量的特征数是重要的。

　　3.给定的参数K。当K的数值很小，比如取2时，很容易得到每个类的收益情况都不佳的结果，因此，适当的增加聚类数可以提高拟合效果，但是当K值过大，也容易造成过拟合，相当于每个类的交易日个数会变得相当少，丧失了模型的通用性。

　　4.特别要注意在对所得到的聚类进行解释的时候，要根据后一天的收益率去评判，也就是这里必须有一个滞后期，否则得到的评判结果对于后续的择时是毫无意义的。

　　

 

'''
机器学习系列策略
K-Means聚类择时
根据K-Means在历史一段时间的聚类结果，对当天的属性进行分类
并根据分类结果所属的类别判断买入/卖出
'''
from sklearn.externals import joblib
from features import gen_attrs

#初始化账户
def initialize(account):
    account.security = '000300.SH'

def handle_data(account,data):
    time = get_last_datetime().strftime("%Y%m%d")
    log.info(time)
    #获取证券过去20日的收盘价数据
    history = get_price(account.security,'',time,'1d',\
                ['open','close','low','high','avg_price','prev_close','volume'],False,'pre')
    # history = data.attribute_history(account.security, ['open','close','low','high','avg_price','prev_close','volume'], 34, '1d')
    log.info(history)
    # 计算当天属性值
    attrs, logreturn = gen_attrs(history, 33)
    # state = 1
    model = joblib.load('kmeans/kmeans.m')
    min_max_scaler = joblib.load('kmeans/std.m')
    attrs = min_max_scaler.transform(attrs)
    state = model.predict(attrs)[-1]
    if state in [0,1,7]:
    # if state in [1, 5, 10] and g.is_pos == 0:
        # order_value('510300.OF',account.cash)
        order_value('159919.OF',account.cash)
        # order_value('510050.OF',account.cash)
        log.info("买入 %s" % (account.security))
        # g.is_pos = 1
    elif state not in [0,1,7]:
    # elif state not in [1, 5, 10] and g.is_pos == 1:
        # order_target('510300.OF',0)
        order_target('159919.OF',0)
        # order_target('510050.OF',0)
        log.info("卖出 %s" % (account.security))
        # g.is_pos = 0

from sklearn.externals import joblib
from sklearn.cluster import KMeans
from sklearn.preprocessing import MinMaxScaler
import numpy as np
import talib
from scipy.stats import boxcox
import features

# history_price = get_price('000300.SH', 'None', '2013-12-31', '1d',['open','close','low','high','avg_price','prev_close','volume'], False, None, 2500,is_panel=1)
history_price = get_price('000300.SH', '2005-01-04', '2013-12-31', '1d',['open','close','low','high','avg_price','prev_close','volume'], False, None)
close = history_price.loc[:, 'close']
prev_close = history_price.loc[:, 'prev_close']
high = history_price.loc[:, 'high']
low = history_price.loc[:, 'low']
train_X, train_logreturn = features.gen_attrs(history_price, 33)
min_max_scaler = MinMaxScaler()
train_X = min_max_scaler.fit_transform(train_X)
joblib.dump(min_max_scaler, 'std.m')
kmeans = KMeans(n_clusters=8, random_state=0, n_init=50, max_iter=1000).fit(train_X)
joblib.dump(kmeans, 'kmeans.m')

Out[18]:

['kmeans.m']