POJ - 1458 Common Subsequence DP最长公共子序列（LCS）

Common Subsequence

A subsequence of a given sequence is the given sequence with some elements (possible none) left out. Given a sequence X = < x1, x2, ..., xm > another sequence Z = < z1, z2, ..., zk > is a subsequence of X if there exists a strictly increasing sequence < i1, i2, ..., ik > of indices of X such that for all j = 1,2,...,k, x _ij = zj. For example, Z = < a, b, f, c > is a subsequence of X = < a, b, c, f, b, c > with index sequence < 1, 2, 4, 6 >. Given two sequences X and Y the problem is to find the length of the maximum-length common subsequence of X and Y.

Input

The program input is from the std input. Each data set in the input contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct.

Output

For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.

Sample Input

abcfbc         abfcab
programming    contest
abcd           mnp

Sample Output

4
2
0

题解出处：http://blog.csdn.net/a_eagle/article/details/7213236

题目大意：给出两个字符串，求两个字符串的最长公共字串。

思路：慢慢重心开始有贪心转向动态规划了，这题就是简单的动态规划题。以题目的第一组测试数据为例。abcfbc abfcab。

辅助空间变化示意图

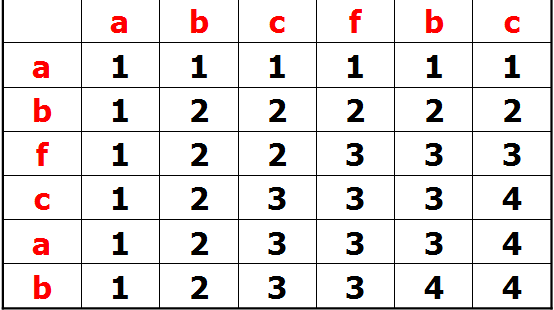
可以看出：

F[i][j]=F[i-1][j-1]+1；（a[i]==b[j]）

F[i][j]=max(F[i-1][j],F[i][j-1])(a[i]!=b[j]);

n由于F(i,j)只和F(i-1,j-1), F(i-1,j)和F(i,j-1)有关, 而在计算F(i,j)时, 只要选择一个合适的顺序, 就可以保证这三项都已经计算出来了, 这样就可以计算出F(i,j). 这样一直推到f(len(a),len(b))就得到所要求的解了.

 

ps:本题求不连续LCS，注释部分为连续LCS。

#include<stdio.h>
#include<string.h>

int f[][];
char s1[],s2[];

int max(int x,int y)
{
    return x>y?x:y;
}

int main()
{
    int n,i,j;
    while(~scanf("%s %s",s1,s2)){
        memset(f,,sizeof(f));
        //int maxx=0;
        for(i=;i<=strlen(s1);i++){
            for(j=;j<=strlen(s2);j++){
                if(s1[i-]==s2[j-]){
                    f[i][j]=f[i-][j-]+;
                    //if(f[i][j]>maxx) maxx=f[i][j];
                }
                //不加else
                else f[i][j]=max(f[i-][j],f[i][j-]);
            }
        }
        //printf("%d\n",maxx);
        printf("%d\n",f[strlen(s1)][strlen(s2)]);
    }
    return ;
}