Tarjan 详解

Tarjan 算法

一.算法简介

Tarjan 算法一种由Robert Tarjan提出的求解有向图强连通分量的算法，它能做到线性时间的复杂度。

我们定义：

如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

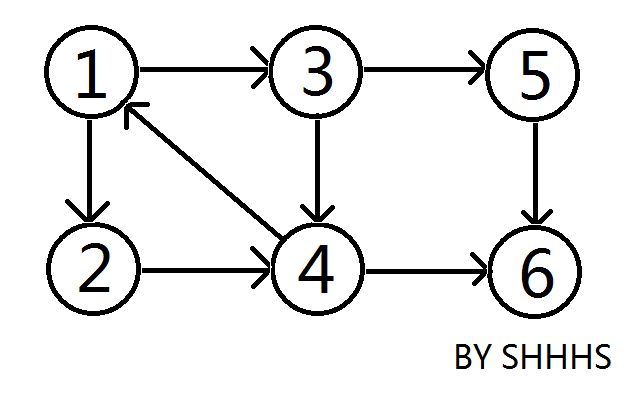
例如：在上图中，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 三个区域可以相互连通，称为这个图的强连通分量。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

再Tarjan算法中，有如下定义。

DFN[ i ] : 在DFS中该节点被搜索的次序(时间戳)

LOW[ i ] : 为i或i的子树能够追溯到的最早的栈中节点的次序号

当DFN[ i ]==LOW[ i ]时，为i或i的子树可以构成一个强连通分量。

二.算法图示

以1为Tarjan 算法的起始点，如图

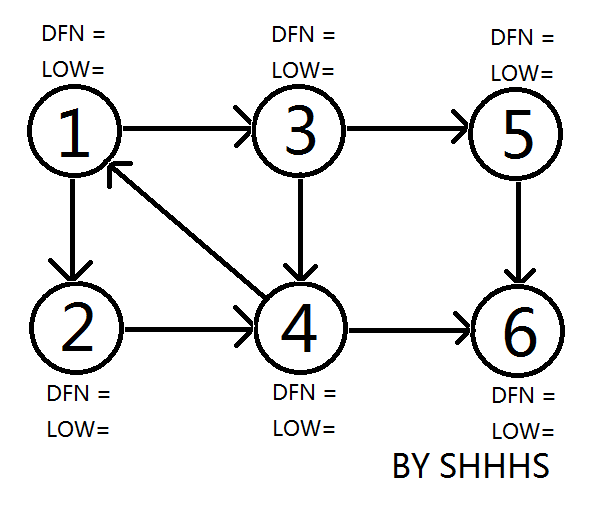
顺次DFS搜到节点6

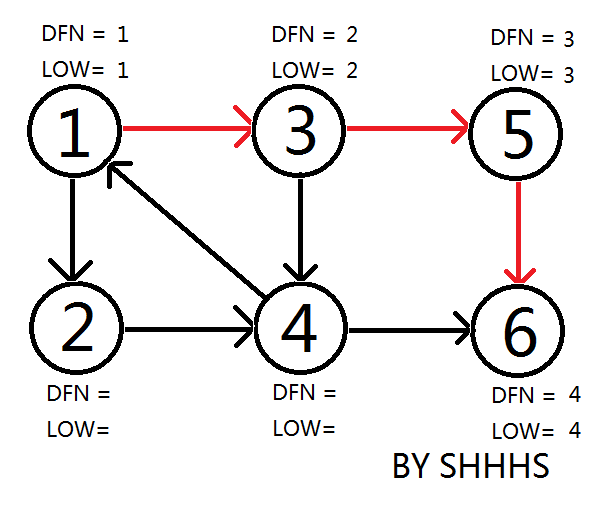
回溯时发现LOW[ 5 ]==DFN[ 5 ] ,  LOW[ 6 ]==DFN[ 6 ] ,则{ 5 } , { 6 } 为两个强连通分量。回溯至3节点，拓展节点4.

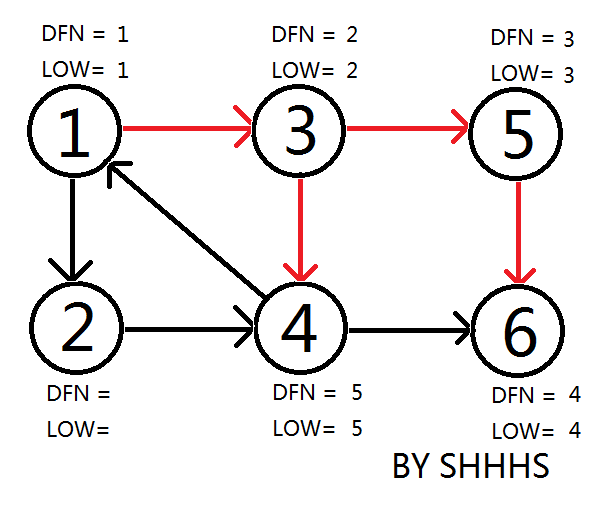
拓展节点1 ， 发现1再栈中更新LOW[ 4 ]，LOW[ 3 ] 的值为1

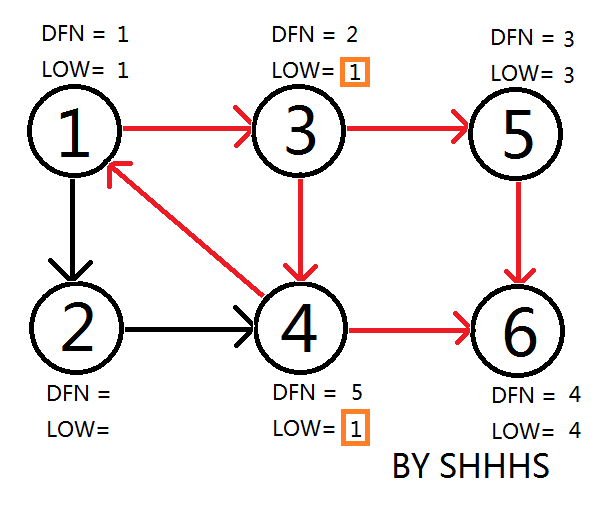
回溯节点1，拓展节点2

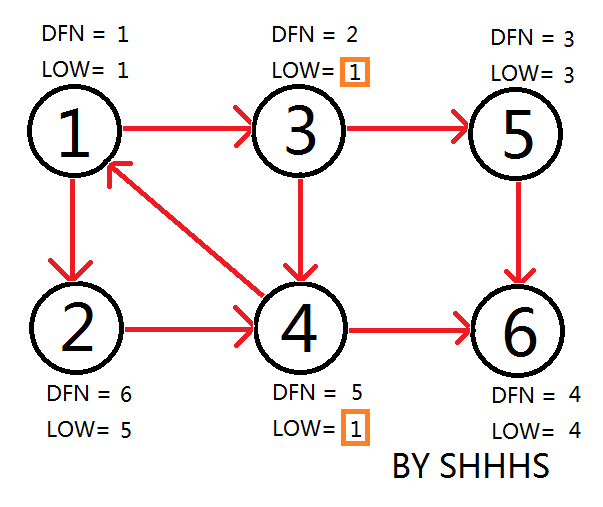
自此，Tarjan Algorithm 结束，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 为图中的三个强连通分量。

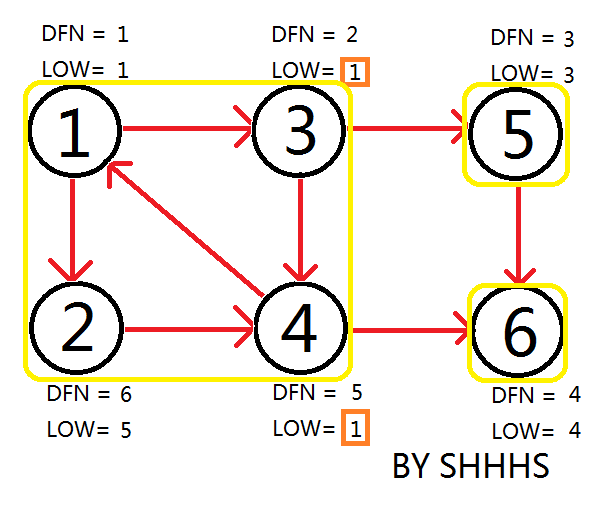
不难发现，Tarjan Algorithm 的时间复杂度为O(E+V).

三.算法模板

void Tarjan ( int x ) {
         dfn[ x ] = ++dfs_num ;
         low[ x ] = dfs_num ;
         vis [ x ] = true ;//是否在栈中
         stack [ ++top ] = x ;
         for ( int i=head[ x ] ; i!= ; i=e[i].next ){
                  int temp = e[ i ].to ;
                  if ( !dfn[ temp ] ){
                           Tarjan ( temp ) ;
                           low[ x ] = gmin ( low[ x ] , low[ temp ] ) ;
                 }
                 else if ( vis[ temp ])low[ x ] = gmin ( low[ x ] , dfn[ temp ] ) ;
         }
         if ( dfn[ x ]==low[ x ] ) {//构成强连通分量
                  vis[ x ] = false ;
                  color[ x ] = ++col_num ;//染色
                  while ( stack[ top ] != x ) {//清空
                           color [stack[ top ]] = col_num ;
                           vis [ stack[ top-- ] ] = false ;
                 }
                 top -- ;
         }
}