【CODEFORCES】 B. Dreamoon and Sets

B. Dreamoon and Sets

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Dreamoon likes to play with sets, integers and 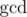.  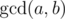is
defined as the largest positive integer that divides both a and b.

Let S be a set of exactly four distinct integers greater than 0.
Define S to be of rank k if
and only if for all pairs of distinct elements si, sjfrom S, .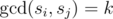

Given k and n,
Dreamoon wants to make up n sets of rank k using
integers from 1 to m such
that no integer is used in two different sets (of course you can leave some integers without use). Calculate the minimum m that makes
it possible and print one possible solution.

Input

The single line of the input contains two space separated integers n, k (1 ≤ n ≤ 10 000, 1 ≤ k ≤ 100).

Output

On the first line print a single integer — the minimal possible m.

On each of the next n lines print four space separated integers representing the i-th
set.

Neither the order of the sets nor the order of integers within a set is important. If there are multiple possible solutions with minimal m,
print any one of them.

Sample test(s)

input

1 1

output

5
1 2 3 5

input

2 2

output

22
2 4 6 22
14 18 10 16

Note

For the first example it's easy to see that set {1, 2, 3, 4} isn't a valid set of rank 1 since .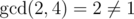

题解：这一题事实上就是找规律。能够发现题目事实上就是要找n堆数，每堆4个并且要互质，能够发现假设依照1 2 3 5，7 8 9 11,13 14 15 17……这样一直构造下去，最后就能够得到解。

#include <iostream>
#include <cstdio>
#include <cstring>

using namespace std;

int d[10005][4],n,k;

int main()
{
    scanf("%d%d",&n,&k);
    for (int i=1;i<=n;i++)
    {
        d[i][0]=6*i-5;
        d[i][1]=6*i-4;
        d[i][2]=6*i-3;
        d[i][3]=6*i-1;
    }
    printf("%d\n",d[n][3]*k);
    for (int i=1;i<=n;i++)
    {
        for (int j=0;j<4;j++) printf("%d ",d[i][j]*k);
        printf("\n");
    }
    return 0;
}