串匹配算法讲解 -----BF、KMP算法

 

参考文章：

http://www.matrix67.com/blog/archives/115    

KMP算法详解

http://blog.csdn.net/yaochunnian/article/details/7059486 

 

1、算法的思想

相比蛮力算法，KMP算法预先计算出了一个next数组，用来指导在匹配过程中匹配失败后尝试下次匹配的起始位置，以此避免重复的读入和匹配过程。这个next数组被叫做“部分匹配值表(**Particial match table**)”，它的设计是算法精妙之处。

对BF算法（每次S、T串都回溯）进行改进，尽量利用已经部分匹配的结果信息，尽量让 i 不回溯，加快模式串的滑动速度。

形象地说,就是假如第i+1个字符匹配失败之后,下一个可能匹配位置至少应该往后挪动多少。

2、部分匹配值表

要理解部分匹配值表，就得先了解字符串的前缀(prefix)和后缀(postfix)。

前缀:除字符串最后一个字符以外的所有头部串的组合。

后缀：除字符串第一个字符以外的所有尾部串的组合。

部分匹配值：一个字符串的前缀和后缀中最长共有元素的长度。

举例说明：字符串ABCAB

前缀：{A， AB， ABC， ABCA}

后缀：{BCAB， CAB， AB， B}

部分匹配值：2 （AB）

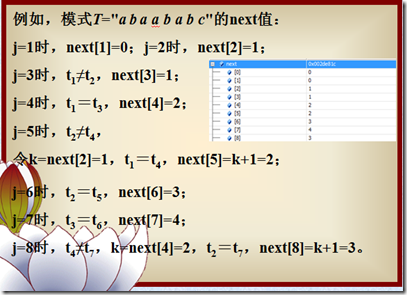
而所谓的部分匹配值表，则为模式串的所有前缀以及其本身的部分匹配值。

还是针对字符串ABCAB，它的部分匹配值表为：

A B C A B

0 0 0 1 2

 

 

啰嗦几句BF算法：

源码如下：包括BF，和KMP。串匹配算法：

   1:  // BF.cpp : 定义控制台应用程序的入口点。

   2:  //

   3:   

   4:  #include "stdafx.h"

   5:  #include "string"

   6:  #include <iostream>

   7:  using namespace std;

   8:   

   9:   

  10:  int index(string s,string t) /*求模式串t在主串s中的定位函数*/

  11:  { 

  12:      int  i,j,m,n;

  13:      i = 0; 

  14:      j = 0;

  15:      n = s.length(); 

  16:      m = t.length();

  17:     while((i<n)&&(j<m))

  18:     {

  19:         if (s[i]== t[j])   

  20:         {

  21:             i++;

  22:             j++;//可以认为是字符匹配成功的次数

  23:         }

  24:         else  

  25:         {

  26:             i = i - j + 1;//可以认为是S当中每次比较的初始位置

  27:             j = 0;

  28:         }

  29:     }

  30:   

  31:    if ( j>=m ) 

  32:        return i - m + 1;

  33:     else   

  34:        return  -1;

  35:  }

  36:   

  37:   

  38:  int  kmp(string s, string t,int next[]) 

  39:  {

  40:      int  i,j,m,n;

  41:      i = 0; 

  42:      j = 0;

  43:      n = s.length(); 

  44:      m = t.length();

  45:      while((i<n) && (j<m)) //循环控制条件

  46:      {

  47:          if (s[i]== t[j])   //如果两者相等，比较下一个字符

  48:          {

  49:             i++;

  50:             j++;

  51:          }

  52:          else               //否则，j = next[j]；

  53:          {

  54:             j = next[j];

  55:          }

  56:      }

  57:      

  58:      if ( j >= m ) //匹配成功，此时j的下标大于等于m

  59:          return i - m + 1;//返回匹配的起始下标

  60:      else   

  61:          return  -1;

  62:      

  63:  }

  64:   

  65:  void  kmpNext(string str,int next[]) 

  66:  {

  67:      next[1]  = 0;

  68:      int j = 1;

  69:      int k = 0;

  70:      while(j < str.length()) 

  71:       {

  72:          if ((k==0) || (str[j-1]==str[k-1])) //第一次匹配或者匹配成功,当t(k)==t(j)

  73:          {

  74:              j++;

  75:              k++;         //继续匹配下一个字符

  76:              next[j] = k;  //相当于next[j] = k + 1;

  77:          }

  78:          else

  79:              k = next[k];  //当t(k)!=t(j),将next[k]给k，然后回溯

  80:       }

  81:  }

  82:   

  83:   

  84:  int main()

  85:   

  86:  {

  87:      string Str,Tsr;

  88:   

  89:      int next[1000]={0,};

  90:      cout <<"请输入S串与T串：" <<endl;

  91:      cin >> Str >> Tsr;

  92:      cout << endl;

  93:      //int flag = index(Str,Tsr);

  94:   

  95:      kmpNext(Tsr,next);

  96:      int  flag =  kmp(Str,Tsr,next);

  97:      if (flag == -1)

  98:      {

  99:          cout << "没有找到子串"<<endl;

 100:      }

 101:      else

 102:      {

 103:          cout << "找到子串的位置为"<< flag <<endl;

 104:      }

 105:   

 106:   

 107:      return 0;

 108:  }

 109:   

.csharpcode, .csharpcode pre
{
font-size: small;
color: black;
font-family: consolas, "Courier New", courier, monospace;
background-color: #ffffff;
/*white-space: pre;*/
}
.csharpcode pre { margin: 0em; }
.csharpcode .rem { color: #008000; }
.csharpcode .kwrd { color: #0000ff; }
.csharpcode .str { color: #006080; }
.csharpcode .op { color: #0000c0; }
.csharpcode .preproc { color: #cc6633; }
.csharpcode .asp { background-color: #ffff00; }
.csharpcode .html { color: #800000; }
.csharpcode .attr { color: #ff0000; }
.csharpcode .alt
{
background-color: #f4f4f4;
width: 100%;
margin: 0em;
}
.csharpcode .lnum { color: #606060; }