S变换

哈哈，这两天在整理时频分析的方法，大部分参考网上写的比较好的资料，浅显易懂，在这谢过各位大神了！

今天准备写下S变换，由于网上资料较少，自己尝试总结下，学的不好，望各位多多指导

由前面的文章可知，傅里叶变换只能作用于收敛信号，短时傅里叶变换的窗函数不可变，小波变换虽然窗函数可变，能进行多分辨率分析，但是其基函数选取困难；S变换介于前两者之间，结合两种方法的优势，可自适应调节分辨率且其逆变换无损可逆。下面详细介绍下S变换：

S变换（ST）是地球物理学家Stockwell域1996年提出的一种时频分析方法，其定义为

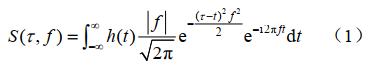
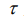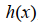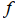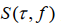式中：为时间，控制窗口函数在时间轴上的位置；为分析信号；为频率；为变换得到的时频谱矩阵。

ST可以写成傅里叶频谱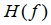的形式：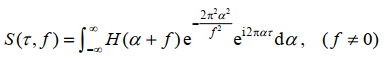

对于离散信号，傅里叶频谱可由式（3）求得。

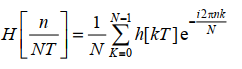
式中：K为离散的时间点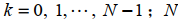，为离散信号长度；T为采样时间间隔。

对于离散信号，令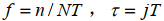，最终离散信号的S变换可以表示为

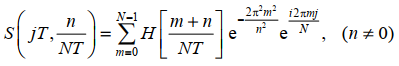
ST克服了STFT窗口时宽不变的缺陷，能根据频率的变化自适应的调整分析时宽和提供直观的时间频率特征，且无须选择窗口函数域分析尺度。

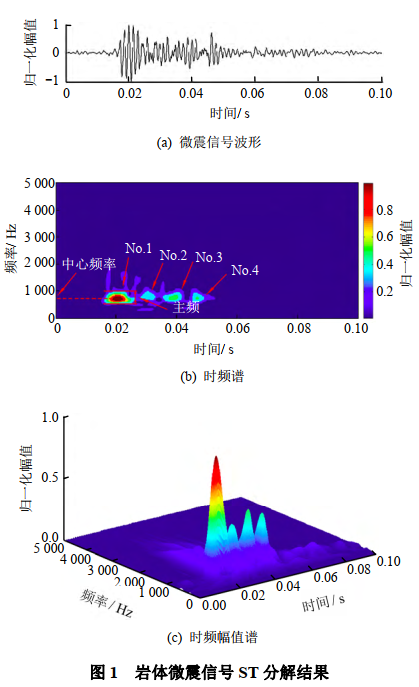
对微震信号进行ST变换，结果如图1所示。图中，振幅采用归一化振幅，其中图1(b)中标出了微震信号频率参数，其中主频为高幅值时频成分对应分布频段，主频段的中心为中心频率

广义S变换公式的推导

对于傅里叶变换，其正变换为

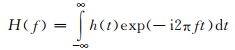
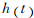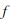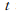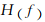式中：为待分析的时间信号序列；表示频率；表示时间；是信号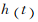的傅里叶变换。

加入对时间序列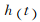加上一个窗函数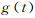，则其谱变为

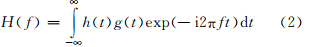
对于S变换，首先定义一个高斯窗函数：

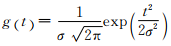      （3）

式中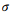：是高斯函数的方差。对公式（2）中的高斯窗函数进行伸缩与平移，可以得到S变换的公式

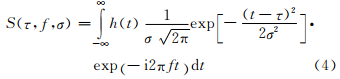
式中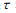：表示高斯窗函数在时间上的平移量。

实际上：s变换就是把小波基函数用高斯窗来代替，又被称为“相位正交”的连续小波变换。

信号 x(t)的S变换 S(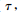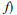定义如下：

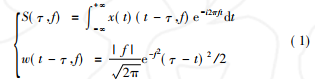
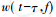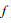式中：为高斯 窗函数；为时移因子，控制高斯窗在时间轴位置；为频率；

由式（1）知，高斯窗口克服了短时傅里叶变换窗口高度和宽度固定的缺陷，其随频率而变化。因此，S变换既可以获得某一时刻的频率信息，又可获得在某一频率上信号的幅值信息。