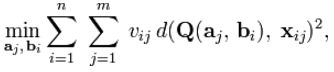Bundle Adjustment光束平差法概述
http://blog.csdn.net/abcjennifer/article/details/7588865
http://blog.csdn.net/ximenchuixuezijin/article/details/7246663
http://blog.csdn.net/peterli_xue/article/details/7528624
给出从不同视角拍摄的,描述同一个场景的一系列图片,bundle adjustment可以根据所有点在图像中的投影作为标准,同时提炼出描述场景结构的3D点坐标、相对运动参数和相机的光学参数。
通常在每个基于feature的3D场景重建算法中都要用到Bundle Adjustment,作为每个基于特征的多视重建视觉算法的最后一步,它是基于3D结构和视角参数(即相机位置,朝向,固有标定和径向畸变)的优化问题,用来获得最佳的三维结构和运动(如相机矩阵)参数估计。提供初始估计,BA同时精化运动和结构参数,通过最小化观测和预测的图像点之间的投影误差。在假定所获得的图像特征中有一些noise的基础上获得最佳重构效果:如果图像feature error服从标准高斯分布,那么Bundle Adjustment就基于最大似然估计。Bundle
Adjustment的名字由来于每个3D特征和相机光学中心“发射”出的光束,而这些光束可以根据结构和视角参数进行最佳调节。
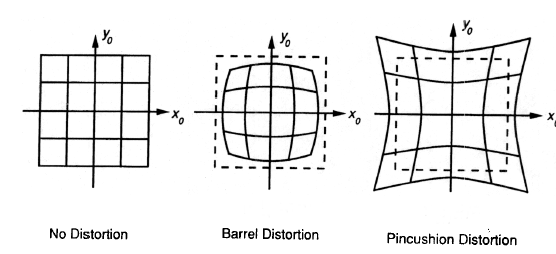
径向畸变:
BundleAdjustment可以将所观测的图像位置和预测的图像位置点进行最小error的映射(匹配),由很多非线性函数的平方和表示(error)。因此,最小化error由非线性最小二乘法实现,Levenberg-Marquardt由其简单实现性和阻尼策略(这样就能使其从初始假设值很快converge到稳定状态)成为最好的方法。通过迭代observed image和predicted image之间的最小距离,L-M方法在线性系统中通过正态方程解决了该问题。
用下式表示BundleAdjustment的工作过程:
其中假设:
n个3D点在m个view(拍摄场景)中,
向量Xij:imgj上的第i个点projection(坐标)这个是实际点坐标
值vij:如果点i在imgj上有映射,则vij=1; elsevij=0;
每个imgj由向量aj参数化 每个3D点由bi参数化
Q(ai,bj):点i在imgj上的predicted projection 这个是理想点坐标
d(x,y):向量x,y的欧式距离
可见,BundleAdjustment可以容忍特征点的丢失。
这个公式的意义就是最小化n个点在两幅图上投影的误差
光束平差法的最终目的归结为:减少观测图像的点和参考图像(预测图像)的点之间位置投影变换(再投影)误差。这最小化误差算法使用的是最小二乘算法,目前使用最为成功是Levenberg-Marquardt, 它具有易于实现,对大范围的初始估计能够快速收敛的优点。
光束法平差(BA)最小化一般通过Levenberg-Marquardt (LM)算法来辅助完成。然而,由于许多未知的因素作用于最小投影误差,一个通用的LM算法的实现(如MINPACK的 lmder)当应用于BA背景下的定义的最小化问题时,会带来极高的计算代价。
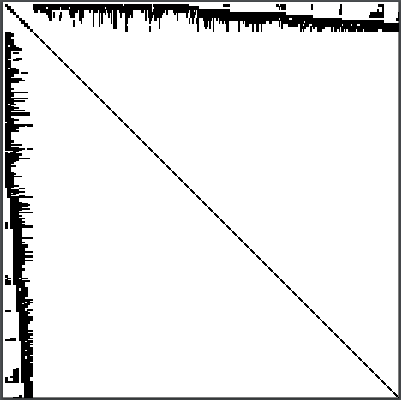
在基本的法方程中不同的三维点和相机参数相互之间影响较小,呈现一种稀疏的块结构(如图)。
一个基于Levenberg-Marquardt(LM)算法的通用稀疏光束法平差Sba利用这种稀疏的特性,使用LM算法的简化的稀疏变量来降低计算的复杂度。Sba是通用的,因为它保证了用户对于相机和三维结构的描述参数的定义的完全控制。因此,它事实上可以支持任何多视重建问题的显示和参数化。比如任意投影相机,部分的或完全标定的相机,由固定的三维点进行外方位元素(即姿态)的估计,精化本征参数,等等。用户要想在这类问题中使用sba,只需要提供合适的程序对这些问题和参数来计算估计的图像投影和他们的函数行列式(Jacobian)。sba包含了检查用户提供的函数行列式的一致性的程序。
Bundle Adjustment光束平差法概述的更多相关文章
- 机器人学 —— 机器人视觉(Bundle Adjustment)
今天完成了机器人视觉的所有课程以及作业,确实是受益匪浅啊! 最后一个话题是Bundle Adjustment. 机器人视觉学中,最顶尖的方法. 1.基于非线性优化的相机位姿估计 之前已经在拟合一篇中, ...
- bundle adjustment原理(1)
那些光束平差的工具,比如SBA.SSBA之类的虽然好,然而例子和教程都不够多且不够详细,让初学者难以上手. 要传入的参数虽然有解释,然而却也不是十分清楚其含义,具体要怎么生成,生成为什么形式. 我在折 ...
- bundle adjustment原理(1)转载
转自菠菜僵尸 http://www.cnblogs.com/shepherd2015/p/5848430.html bundle adjustment原理(1) 那些光束平差的工具,比如SBA.SSB ...
- bundle adjustment 玩具程序
结合 bundle adjustment原理(1) 和 Levenberg-Marquardt 的 MATLAB 代码 两篇博客的成果,调用MATLAB R2016a中 bundleAdjustmen ...
- 数据结构Java实现01----算法概述
[声明] 欢迎转载,但请保留文章原始出处→_→ 生命壹号:http://www.cnblogs.com/smyhvae/ 文章来源:http://www.cnblogs.com/smyhvae/p/4 ...
- VIO的Bundle Adjustment推导
IMU模型和运动积分 $R_{\tiny{WB}} \left( t +\Delta{t} \right) = R_{\tiny{WB}} \left( t \right) Exp\left( \in ...
- SLAM学习笔记(1)基本概念
SLAM (simultaneous localization and mapping),也称为CML (Concurrent Mapping and Localization), 即时定位与地图构建 ...
- SLAM论文阅读笔记
[1]陈卫东, 张飞. 移动机器人的同步自定位与地图创建研究进展[J]. 控制理论与应用, 2005, 22(3):455-460. [2]Cadena C, Carlone L, Carrillo ...
- Ceres Solver: 高效的非线性优化库(二)实战篇
Ceres Solver: 高效的非线性优化库(二)实战篇 接上篇: Ceres Solver: 高效的非线性优化库(一) 如何求导 Ceres Solver提供了一种自动求导的方案,上一篇我们已经看 ...
随机推荐
- LeetCode(16)题解--3Sum Closest
https://leetcode.com/problems/3sum-closest/ 题目: Given an array S of n integers, find three integers ...
- 点击其它地方关闭DIV
<!DOCTYPE html> <html> <head> <meta charset="utf-8" /> <title&g ...
- SAM4E单片机之旅——12、USART
清楚了UART的用法之后,现在来研究一下USART的用法.和上一次差不多,这次也通过USART的串口来实现和PC的通信.和上一次不同的是,USART本身就有接收超时的功能,所以这次就不用TC了. US ...
- leetcode题目解答报告(1)
Remove Element 题目: Given an array and a value, remove all instances of that value in place and retur ...
- Spark SQL includes a cost-based optimizer, columnar storage and code generation to make queries fast.
https://spark.apache.org/sql/ Performance & Scalability Spark SQL includes a cost-based optimize ...
- Node中的Socket.IO 简单Demo及说明
注:下面Demo的Server和Client都是纯后端. 并没有web页面. Server端代码: var express = require('express'); var app = expres ...
- git文章列表
关于gitlab默认clone协议 Git实现从本地加入项目到远程仓库 翻翻git之---一个简单的标签控件 LabelView (随手发了两张小宝宝的玩耍照) id=1125" targe ...
- SpringSecurityLDap
ldap,用于用户登录的权限管理, 可参考:http://www.cnblogs.com/icuit/archive/2010/06/10/1755575.html
- 使用jQuery集成Google翻译
利用jQuery,轻松将google翻译集成到你的web应用中. 1. [代码][JavaScript]代码 1<script src="Scripts/Translator ...
- HTML标签深入学习系列(1)——注释标签 <!-- -->
一.HTML注释的语法 <!--注释内容--> 二.HTML注释的用处 1.普通注释(增强代码的可读性) 方便别人:方便其它程序员了解你的代码 方便自己:方便以后对自己代码的理解与修改等等 ...