论文选读二：Multi-Passage Machine Reading Comprehension with Cross-Passage Answer Verification

论文选读二：Multi-Passage Machine Reading Comprehension with Cross-Passage Answer Verification

目前，阅读理解通常会给出一段背景资料，据此提出问题，而问题的答案也往往在背景资料里。不过背景资料一般是一篇文章，或者是文章的一个段落。而对于多篇文章，特别是多篇相近文章时，当前的模型效果就不那么明显了。本文即针对此问题提出的解决方案。此文提出的模型包含三个部分：答案提取模块，答案评价模块，与答案交叉验证模块。

本文提出一个假设：问题的正确答案往往会出现在多篇文章中，且有通性，而不正确的答案则通常会与众不同。

（这个场景正对应我们平常在搜索引擎中的搜索。当键入我们想要找的内容，会命中很多内容，而通常其中只有一项是我们真正需要的，因此我们会多个答案对比，从而找到最终想要的。）

本文提出的模型即基于这个假设。当提出一个问题后，有多篇文章命中，或者说针对多篇文章提出一个问题，首先分别在每篇文章中提取回答，即确定候选回答在文章中的位置；其次， 用打分函数对每个答案进行打分，即对每个候选回答的内容进行评价，最后，再对比每个回答，让每个回答相互验证。这三步会共同决定最终的答案。

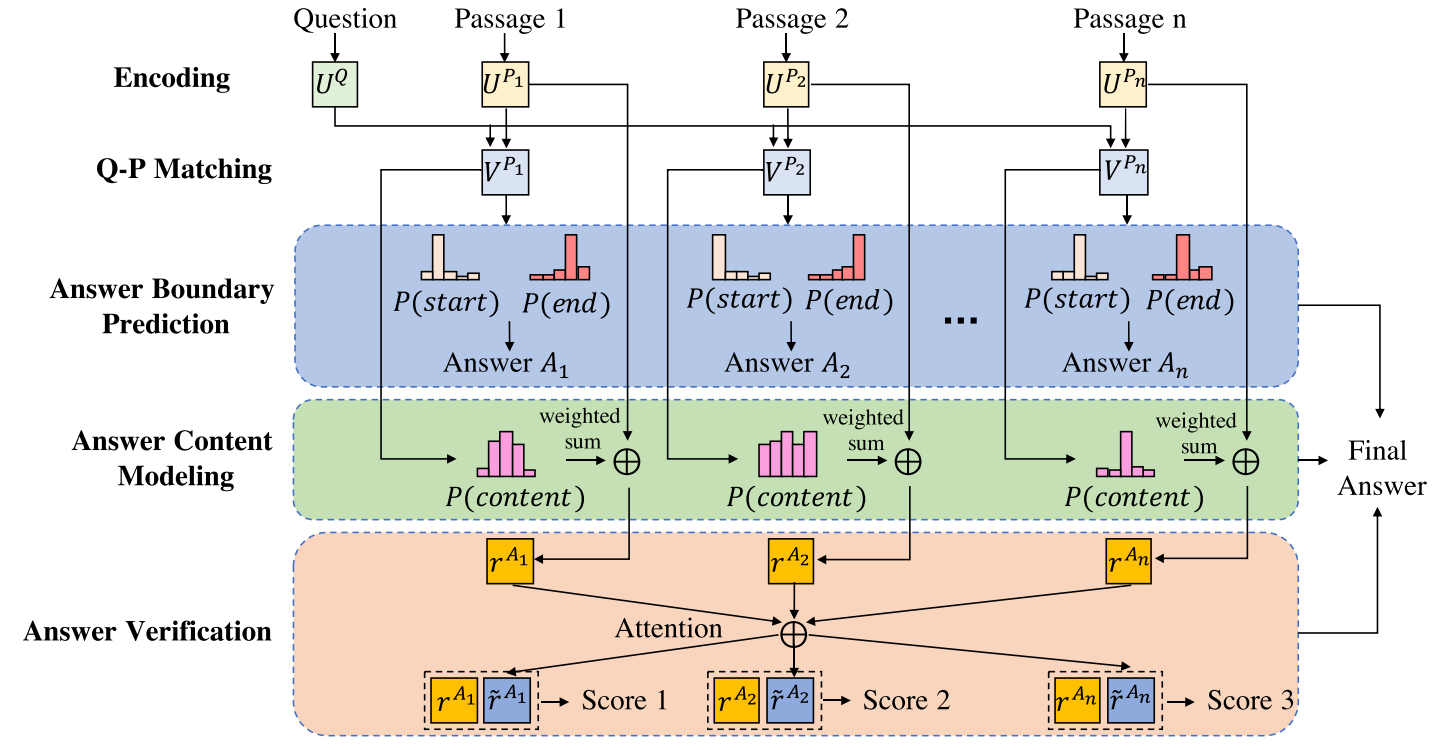
对于给定的问题Q与对应的文章集\(\{P_i\}\)，我们希望找到Q最恰当的答案。

第一个模块:

编码：将所有单词向量化（主要是字符向量和与词向量拼接)，然后，用biLSTM处理问题与文章集:
\[
u_t^Q = BiLSTM_Q(u_{t-1}^Q, [e_t^Q, c_t^Q])\\
u_t^{P_i} = BiLSTM_P(u_{t-1}^{P_i},[e_t^{P_i},c_t^{P_i}])
\]
其中\(e_t, c_t\)分别是第t个词的词向量与字符向量，可以看出，每篇文章是单独训练的。

Q-P Matching: 接下来将Q 与Ps联系起来，目前来说，就一定是context-to-question attention layer了。 这里使用的是attention flow layer产生一个混淆矩阵：
\[
S_{t,k} = u_t^{Q^T}\cdot u_k^{P_i}
\]
接下来按 Seo et al的方法得到 c2q attention:
\[
a_t = softmax(S_{t:})\\
\tilde{U}_{:t}^{P_i} = \sum_j a_{tj}\cdot U_{:j}^{P_i}
\]
然后，再经过一biLSTM得到新的内部表示：
\[
v^{P_i}_t = BiLSTM_M(v_{t-1}^{P_i}, \tilde{u}_t^{P_i})
\]
Answer Boundary Prediction: 有了上述的内部表示，第一个模块终于可以给出答案在文章中位置的预测了：
\[
g_k^t = w_1^{aT}\tanh (W_2^a [v_k^P, h_{t-1}^a])\\
\alpha_k^t = \exp(g_k^t)/\sum_{j =1 }^{|P|}\exp(g_j^t)\\
c_t = \sum_{k = 1}^{|P|} a_k^t\cdot v_k^P\\
h_t^a = LSTM(h_{t-1}^a,c_t)
\]
则第一部分的loss：
\[
L_{boundary} =- \frac{1}{N}\sum_{i = 1}^N (\log\alpha_{y_i^1}^1 +\log\alpha_{y_i^2}^2)
\]
其中$y_i^1,y_i^2为第i篇文章的起点与终点。

第二模块：

此模块对上一模块得到的候选答案进行评分，对每个候选答案的每个词判断其是否在应该出现在答案中：
\[
p_k^c = sigmoid(w_1^c ReLU(W_2^2v_k^{P_i}))
\]
此为第k个词出现在答案中的概率。

那损失为：
\[
L_{content} = - \frac{1}{N}\frac{1}{|P|}\sum_{i=1}^N\sum_{j = 1}^{|P|}[y_k^c \log p_k^c + (1 - y_k^c)\log(1 - p_k^c)]
\]

第三模块：

这一模块对所有候选答案进行attention,从而找到最佳答案. 每篇文章的候选答案可以这样表示：
\[
r^{A_i} = \frac{1}{|P_i|} \sum_{k = 1}^{|P_i|}p_k^c[e_k^{P_i},c_k^{P_i}]
\]
应用attention:

\[
\begin{equation}
s_{i,j} = \left\{
\begin{array}{lr}
0, \ \ \ \ if\ \ i = j, & \\
r^{A_i^T}\cdot r^{A_j}, \ \ \ \ otherwise, &
\end{array}
\right.
\end{equation}
\\
\alpha_{i,j} = \exp(s_{i,j})/\sum_{k = 1}^n \exp(s_{i,k})\\
\tilde{r}^{A_i} = \sum_{j = 1}^n \alpha_{i,j}^{A_j}\\
p_i^v = \exp(g_i^v)/ \sum_{j = 1}^n \exp(g_j^v)\\
L_{verify} = -\frac{1}{N}\sum_{i = 1}^N\log p_{y_i^v}^v
\]

最后，整个模型的损失：

\[
L = L_{boundary} + \beta_1 L_{content} + \beta_2 L_{verify}
\]

其中\(\beta_1, \beta_2\)为超参。

评：

本文对多篇文章的阅读理解，使用attention的方式选择是最优答案，是一个不错的思路。