[BZOJ3167]Sao

Problem

给你n个任务，n-1个关系，a<b或者a>b代表a在b前或者a在b后

问你有几种拓扑序

Solution

f[i][j]表示第i个节点前有j个节点的方案数

设当前节点为x，儿子节点为s，若x依赖于s，那么



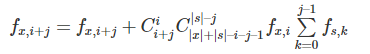
若s依赖于x，那么

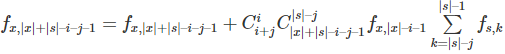
Notice

要预处理出C数组

Code

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define sqz main
#define ll long long
#define reg register int
#define rep(i, a, b) for (reg i = a; i <= b; i++)
#define per(i, a, b) for (reg i = a; i >= b; i--)
#define travel(i, u) for (reg i = head[u]; i; i = edge[i].next)
const int INF = 1e9, N = 1000, mo = INF + 7;0
const double eps = 1e-6, phi = acos(-1);
ll mod(ll a, ll b) {if (a >= b || a < 0) a %= b; if (a < 0) a += b; return a;}
ll read(){ ll x = 0; int zf = 1; char ch; while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if (ch == '-') zf = -1, ch = getchar(); while (ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar(); return x * zf;}
void write(ll y) { if (y < 0) putchar('-'), y = -y; if (y > 9) write(y / 10); putchar(y % 10 + '0');}
int f[N + 5][N + 5], g[N + 5][N + 5], now[N + 5], Size[N + 5], num = 0, head[N + 5], C[N + 5][N + 5];
struct node
{
    int vet, val, next;
}edge[2 * N + 5];
void add(int u, int v)
{
    edge[++num].vet = v;
    edge[num].next = head[u];
    edge[num].val = 0;
    head[u] = num;
    edge[++num].vet = u;
    edge[num].next = head[v];
    edge[num].val = 1;
    head[v] = num;
}
void dfs(int u, int fa)
{
    Size[u] = f[u][0] = 1;
    travel(i, u)
    {
        int v = edge[i].vet;
        if (v == fa) continue;
        dfs(v, u);
        memset(now, 0, sizeof now);
        if (edge[i].val)
        {
            rep(j, 0, Size[u])
                rep(k, 0, Size[v])
                    now[j + k] = (now[j + k] + (ll)C[j + k][j] * C[Size[u] + Size[v] - j - k - 1][Size[v] - k]
                                % mo * f[u][j] % mo * g[v][k - 1] % mo) % mo;
        }
        else
        {
            rep(j, 0, Size[u])
                rep(k, 0, Size[v])
                    now[Size[u] + Size[v] - j - k - 1] = (now[Size[u] + Size[v] - j - k - 1] + (ll)C[j + k][j] * C[Size[u] + Size[v] - j - k - 1][Size[v] - k]
                                % mo * f[u][Size[u] - j - 1] % mo * (g[v][Size[v] - 1] - g[v][Size[v] - k - 1] + mo) % mo) % mo;
        }
        Size[u] += Size[v];
        rep(j, 0, Size[u]) f[u][j] = now[j];
    }
    g[u][0] = f[u][0];
    rep(i, 1, Size[u]) g[u][i] = (g[u][i - 1] + f[u][i]) % mo;
}
int sqz()
{
    int H_H = read();
    rep(i, 0, N)
    {
        C[i][0] = 1;
        rep(j, 1, i)
            C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % mo;
    }
    while (H_H--)
    {
        int n = read();
        num = 0;
        memset(head, 0, sizeof head);
        rep(i, 1, n - 1)
        {
            int u, v; char op;
            scanf("%d %c %d", &u, &op, &v);
            if (op == '>') swap(u, v);
            add(u, v);
        }
        dfs(0, -1);
        printf("%d\n", g[0][n - 1]);
    }
}