机器学习基石8-Noise and Error

注：
文章中所有的图片均来自台湾大学林轩田《机器学习基石》课程。
笔记原作者：红色石头
微信公众号：AI有道

上一节课，我们主要介绍了VC Dimension的概念。如果Hypotheses set的VC Dimension是有限的，且有足够多的资料$N$，同时能够找到一个hypothesis使它的$E_{in}\approx 0$，那么就能说明机器学习是可行的。本节课主要讨论数据集有Noise的情况下，是否能够进行机器学习，并且介绍了假设空间H下演算法$\mathcal{A}$的Error估计。

一、Noise and Probablistic target

上节课推导VC Dimension的数据集是在没有Noise的情况下，本节课讨论如果数据集本身存在Noise，那VC Dimension的推导是否还成立呢？
首先，Data Sets的Noise一般有三种情况：

由于人为因素，正类被误分为负类，或者负类被误分为正类；
同样特征的样本被模型分为不同的类；
样本的特征被错误记录和使用。

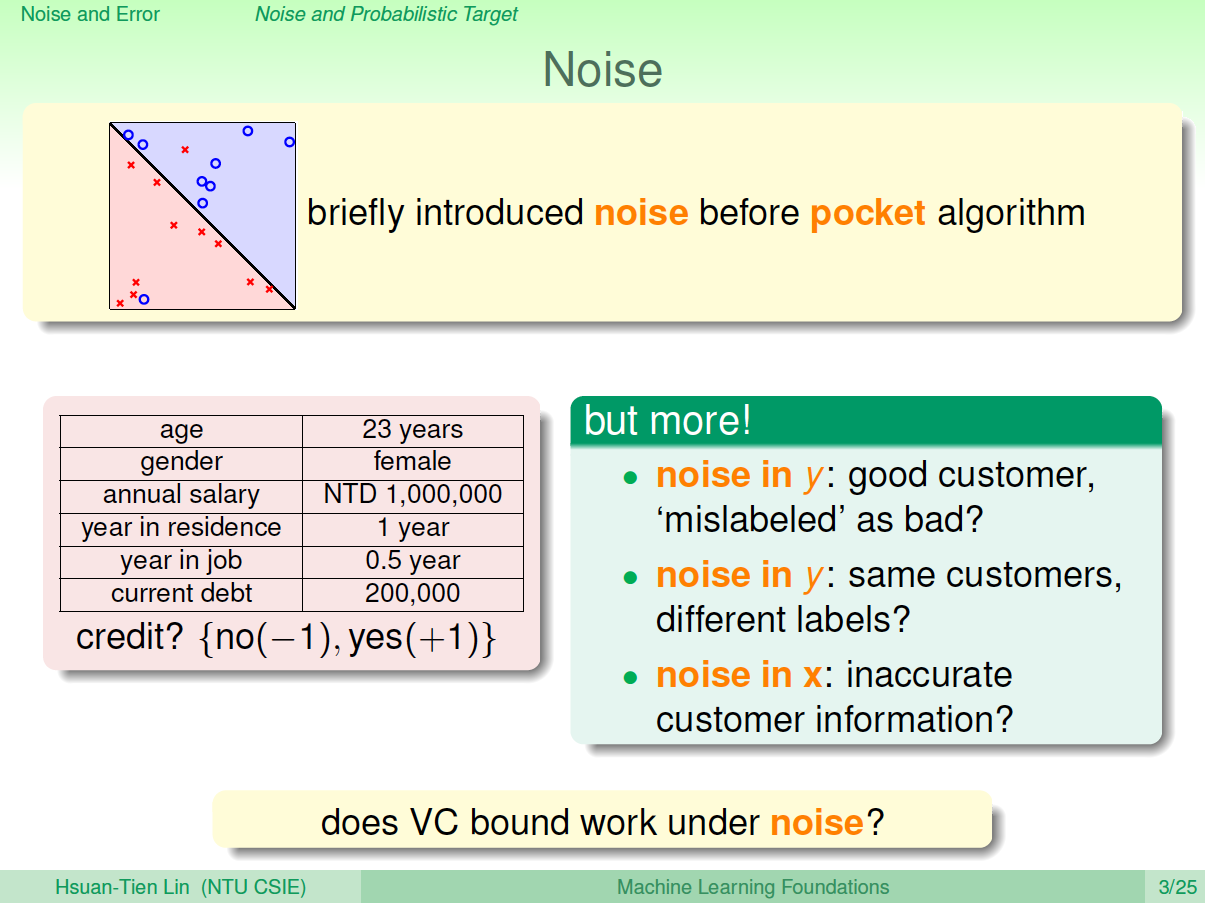
之前的数据集是确定的，即没有Noise的，我们称之为Deterministic。现在有Noise了，也就是说在某点处不再是确定分布，而是概率分布了，即对每个$(x,y)$出现的概率是$P(y|x)$

因为Noise的存在，例如在x点，有$0.7$的概率$y=1$，有$0.3$的概率$y=0$，即$y$是按照$P(y|x)$分布的。数学上可以证明如果数据集按照$P(y|x)$概率分布且是iid（Independent and identically distributed，独立同分布）的，那么以
前证明机器可以学习的方法依然奏效，VC Dimension有限即可推断$E_{in}$和$E_{out}$是近似的。

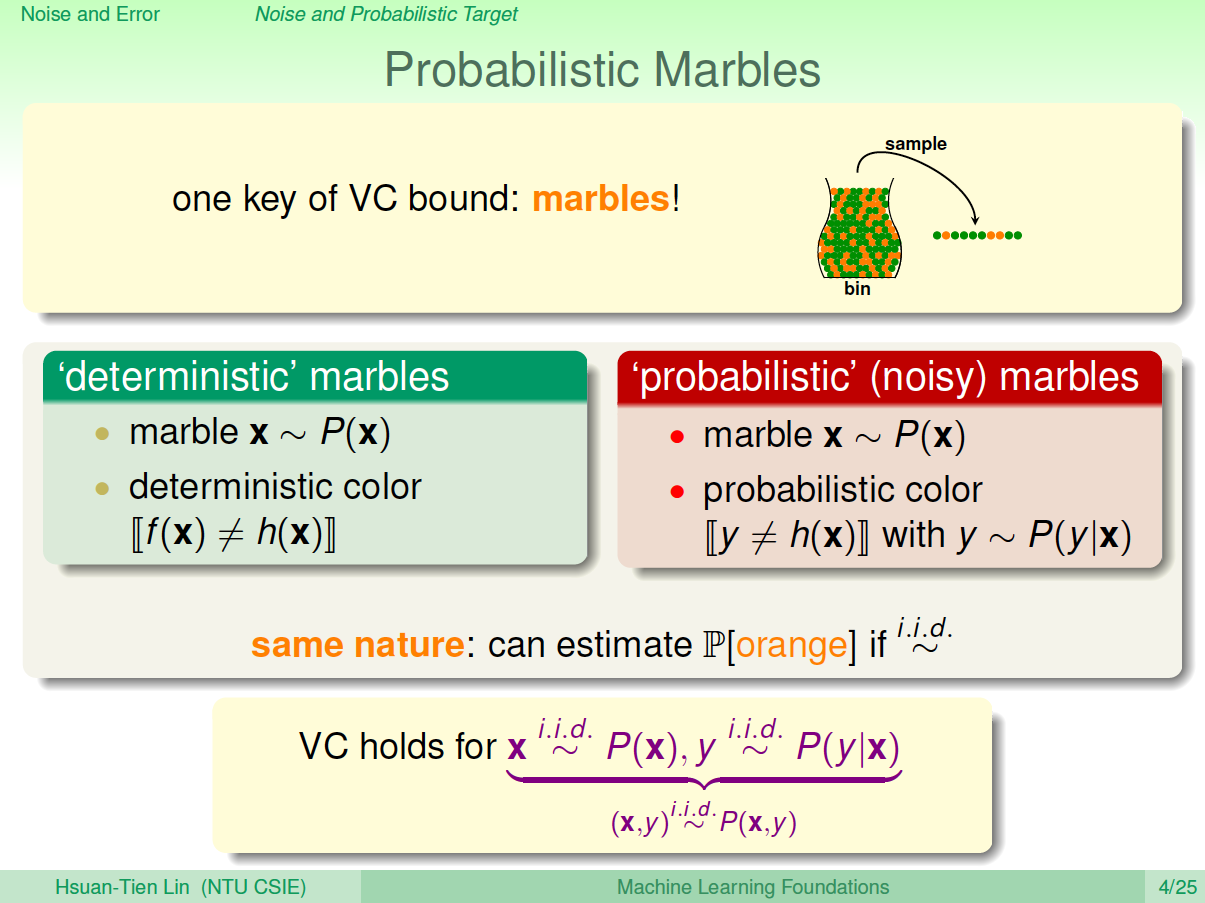
$P(y|x)$称为目标分布（Target Distribution）。它实际上告诉我们最好的选择是什么，同时伴随着多少noise。其实，没有noise的数据仍然可以看成“特殊”的概率分布，即概率仅是1和0。对于以前确定的数据集：\[P(y|x)=\begin{cases}1, f(x)=y\\ 0, f(x)\neq y\end{cases}\]

在引入noise的情况下，新的学习流程图如下所示：

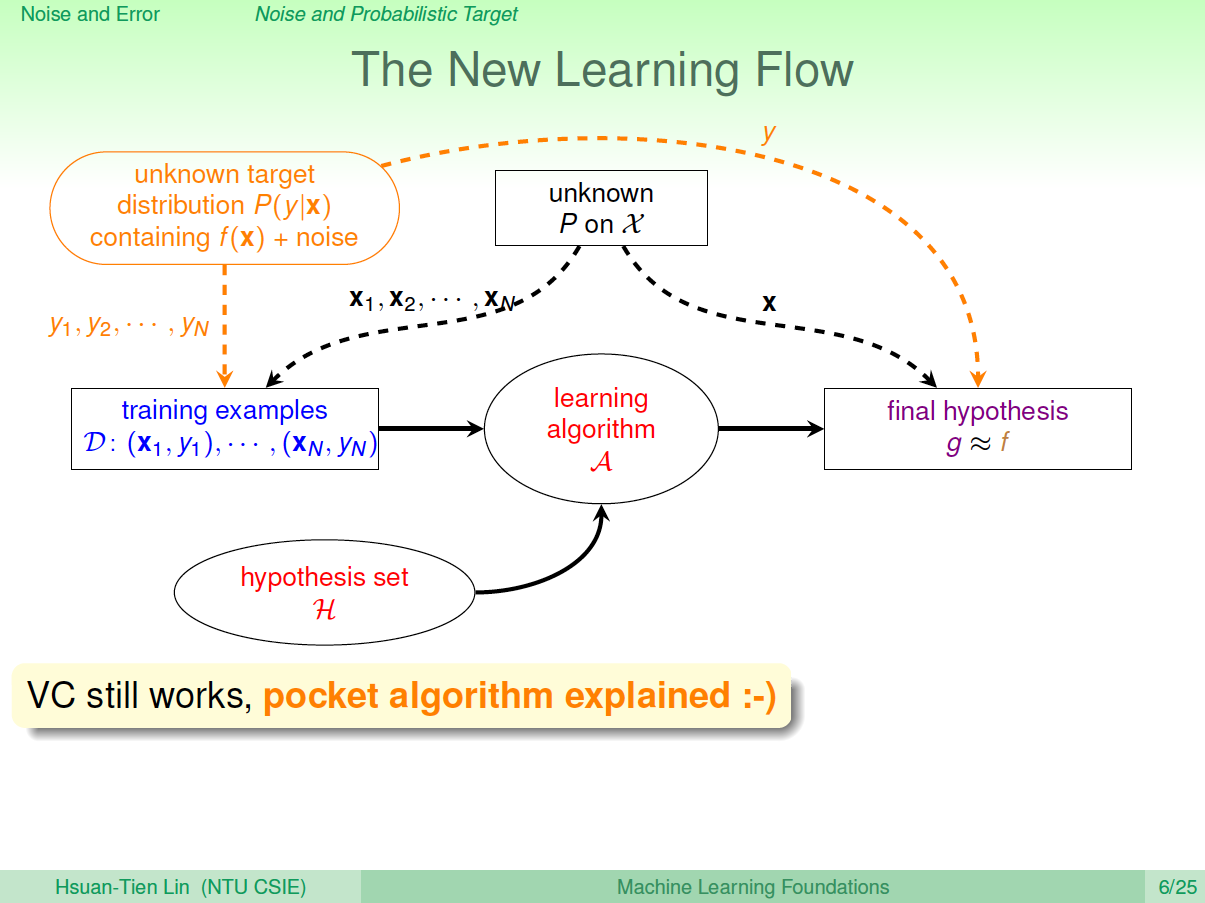
Error Measure

机器学习需要考虑的问题是找出的$g$与目标函数$f$有多相近，我们一直使用$E_{out}$进行误差的估计，那一般的错误测量有哪些形式呢？
我们介绍的$g$对错误的衡量有三个特性：

out-of-sample: 样本外的未知数据
pointwise: 对每个数据点进行测试
classification: 看prediction与target是否一致，classification error通常称为$0/1$ error

pointwise error是对数据集的每个点计算错误并计算平均，$E_{in}$和$E_{out}$的pointwise error的表达式为：

pointwise error是机器学习中最常用也是最简单的一种错误衡量方式，未来课程中，主要考虑这种方式。pointwise error一般可以分成两类：$0/1$ error和squared error。$0/1$ error通常用在分类（classification）问题上，而squared error通常用在回归（regression）问题上。

Ideal Mini-Target由$P(y|x)$和err共同决定，0/1 error和squared error的Ideal Mini-Target计算方法不一样。例如下面这个例子，分别用0/1 error和squared error来估计最理想的mini-target是多少。0/1 error中的mini-target是取P(y|x)最大的那个类，而squared error中的mini-target是取所有类的加权平方和。

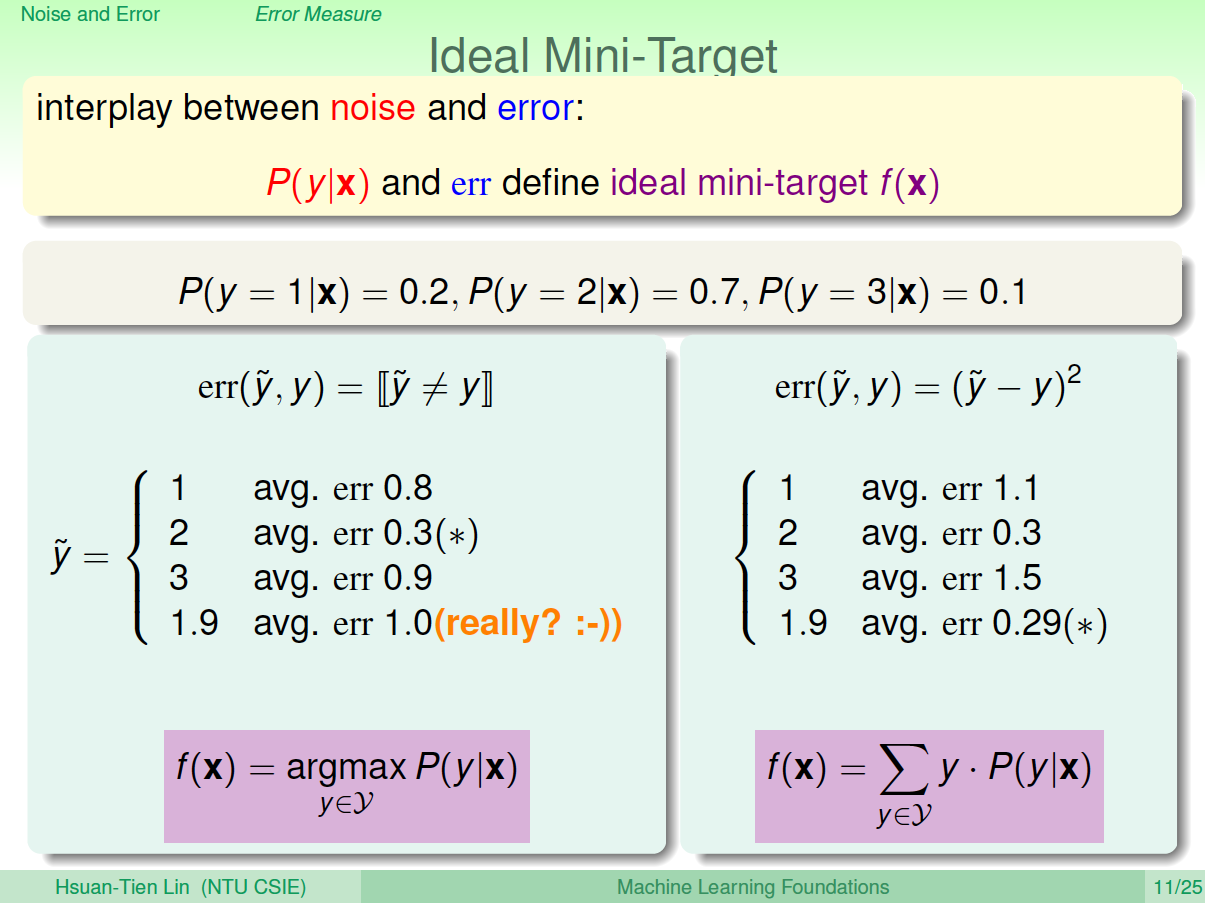
有了错误衡量，就会知道当前的$g$是好还是不好，并会让演算法不断修正，得到更好的$g$，从而使得$g$与目标函数更接近。所以，引入error measure后，学习流程图如下所示：

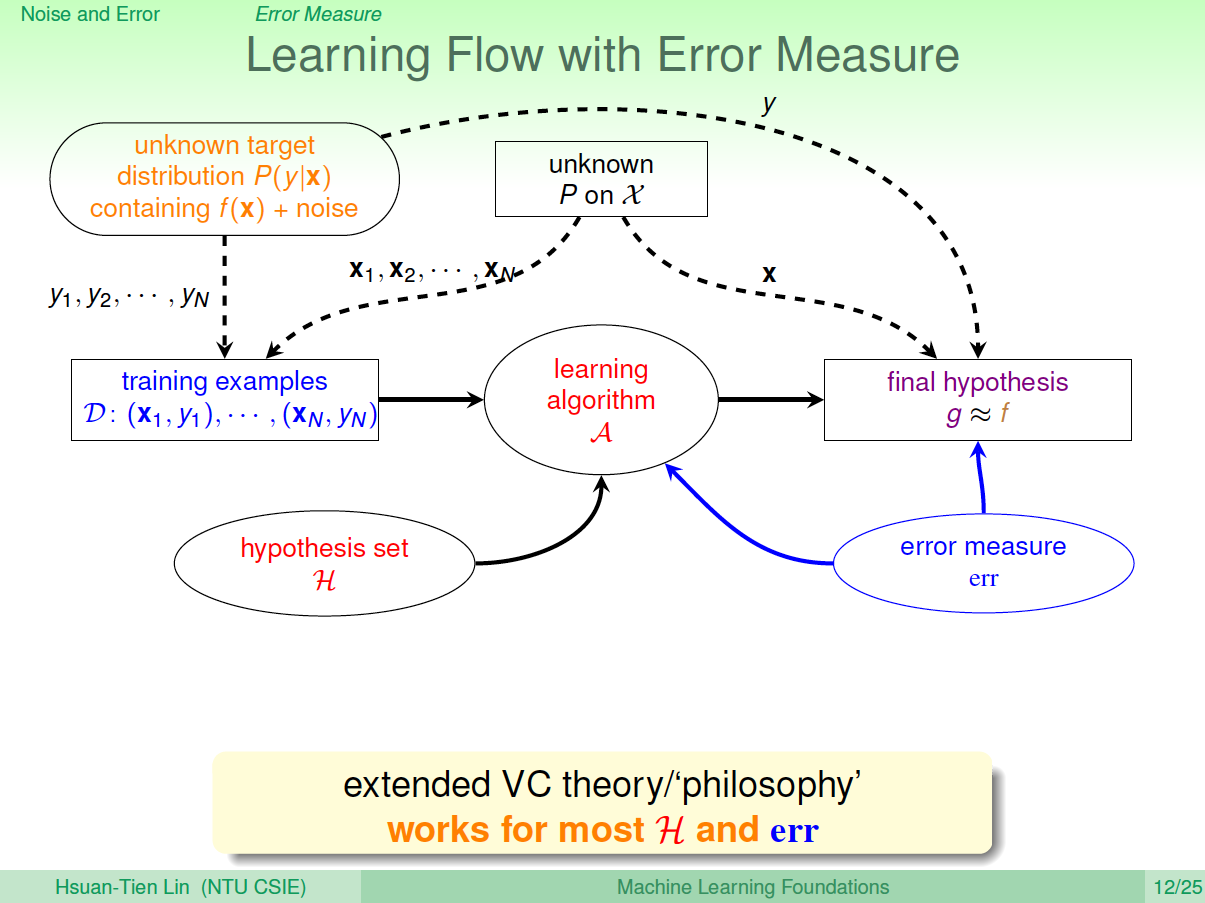
三、Algorithmic Error Measure

Error有两种：false accept和false reject。false accept意思是误把负类当成正类，false reject是误把正类当成负类。根据不同的机器学习问题，false accept和false reject应该有不同的权重，这与实际情况是符合的，比如是超市优惠，那么false reject应该设的大一些；如果是安保系统，那么false accept应该设的大一些。

机器学习演算法$\mathcal{A}$的cost function error估计有多种方法，真实的err一般难以计算，常用的方法可以采用plausible或者friendly，根据具体情况而定。

引入algorithm error measure 之后，学习流程图如下：

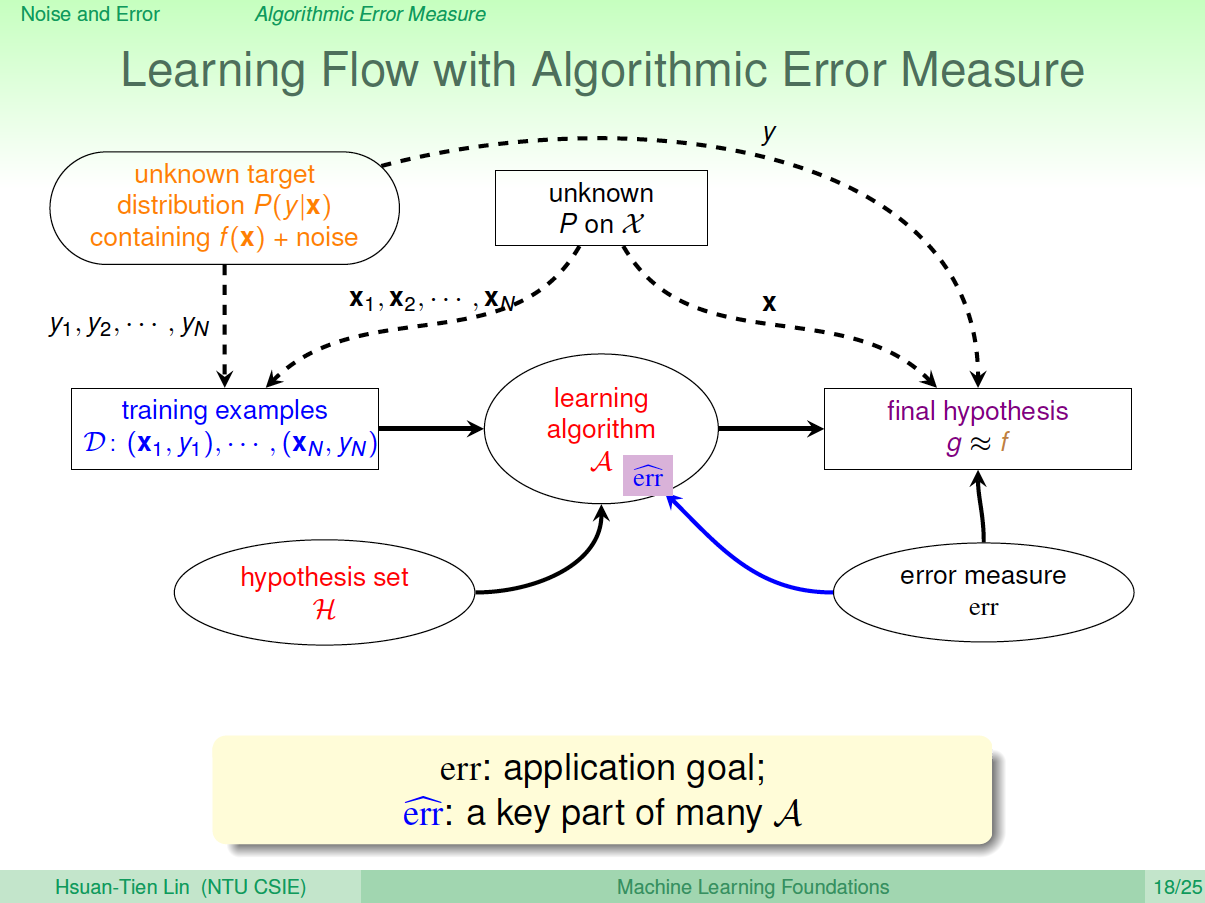
四、Weighted Classification

实际上，机器学习的Cost Function即来自于这些error，也就是算法里面的迭代的目标函数，通过优化使得Error（$E_{in}$）不断变小。cost function中，false accept和false reject应该赋予不同的权重。那么在感知器学习算法和贪心算法中如何体现？对线性可分的数据集，PLA算法不受影响，因为最终$E_{in}=0$。对线性不可分的数据集，使用贪心算法，但对加权的$E^{0/1}_{in}$，贪心算法应该如何进行?

对不同权重的错误惩罚，可以选用virtual copying的方法。

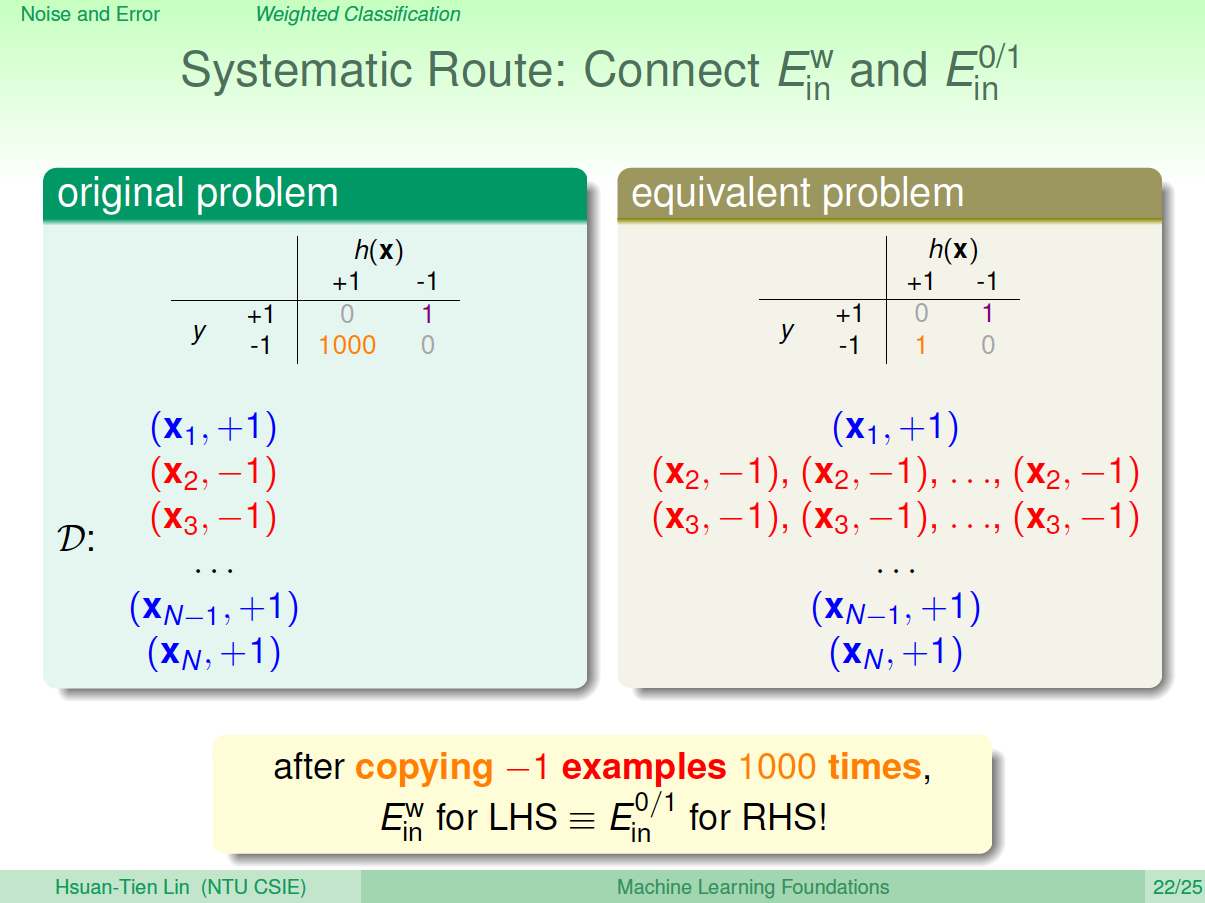
五、总结

本节课主要讲了在有Noise的情况下，即数据集按照$P(y|x)$概率分布，那么VC Dimension仍然成立，机器学习算法推导仍然有效。机器学习cost function常用的Error有0/1 error和squared error两类。实际问题中，对false accept和false reject应该选择不同的权重。