关于SVD

下面的公式是基于物品的计算：

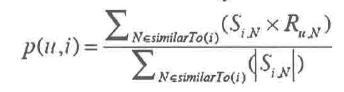
我之所以要把粘出来，是因为这种计算模式是公式界常用的一种方式：体会一下，单个来讲SiN*Run / |Sin|，分子分母公约之后只剩下了Run了；但是公式记录的是一种和运算，所以这就代表Run的某种运算，试想，如果两个物品完全相同，那么真的就是可以分子分母约分；那评分本来就是应该一样的；

当然没有两个物品是完全相似的。

 

U是用于行压缩（减少样本数），V是用于列压缩（降维）

 

通过压缩图像的例子，我们看出来其实本质来讲最终输出的内容是一致的（无论是压缩还是不压缩）；但是关键在于压缩的过程中，正常模式要构建一个32*32的像素点阵要1024个数据；但是如果会用svd，你会发现其实只是需要两个32 * 2（U和VT)以及2个奇异值（如果算上0值是4个数据），搞掂；压缩了将近10倍。

其实SVD最迷人的地方还是在存储上，就像上面说的正常要存储1024个点，但是基于SVD，只需要存储130个点就可以了，比如只是存储U，S，VT，只有在需要的时候计算一下就可了。

 

下面介绍一下SVD的原理；讲解SVD原理之前，想要介绍几个线性代数的概念：首先是向量的长度和角度；向量的长度又称之为向量的模，是向量元素（坐标）的平方和的根。

至于向量的角度，就是在当前坐标系向，向量和坐标轴的夹角（向量的角度并没有明确的定义，可以这样来理解）。

下面再来说说正交矩阵；正交矩阵是这样的来的；作为一个向量A，在e1，e2坐标系下；然后现在还有另外一个坐标系，我们称之为e1'，e2'，在此坐标系下构建一个向量A'，这个A'要和A重合，虽然是两个不同的坐标系，但是A和A'在e1，e2坐标系下来看和A是同一个位置；

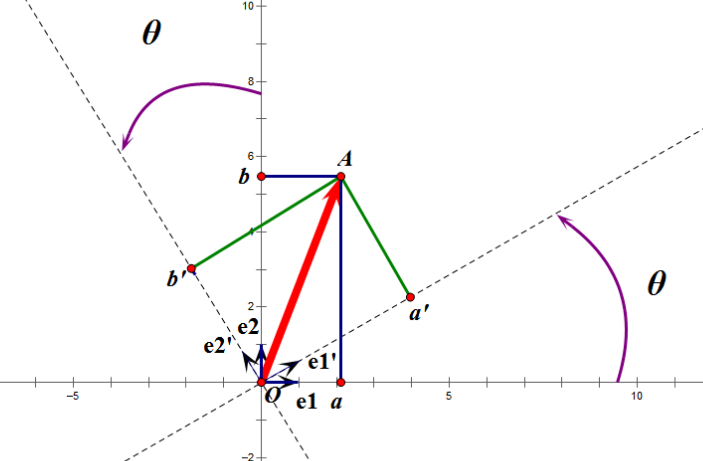
这里就存在一个映射关系，然后，对于e1'，e2'的坐标系：

(a',b').T=U*(a,b).T

这里的U就是一个正交矩阵。那么怎么来计算这个U呢？

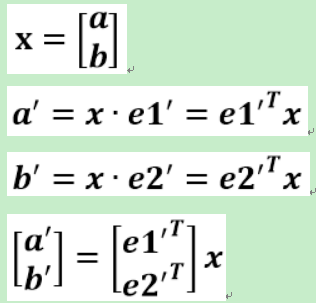
观察一下上面的图，e1'在e1的映射中，x轴代表sinx，y周代表cosx（夹角对应边的映射是sin，非夹角对应边是cos，建立e1'，和e2'的值，注意夹角寻找θ）：

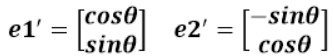
这样，由上面的一系列过程我们就推知了U值，因为U值就是：

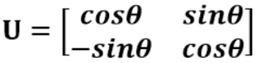
为什么是这个值？因为U是（参看上面的推导）：

其实这里正在讲的是线性代数和空间几何中常见的一种场景：正交旋转。将一个坐标系旋转到另外一个坐标系下，这个变换，也叫做正交变换。

正交矩阵完事了，在讲述SVD之前还要在介绍一个计算：EVD（eigenvalue decomposition），特征值分解。

我们介绍一下EVD的一个特例，EVD我们知道是Ax = λx（在PCA小节中曾经提到过，那个时候使用的v，本节使用的x），给定了向量A，右乘一个x等价于与一个标量λ右乘一个x；其中λ称之为特征值，x称之为特征向量。这里我们拿一个特例来说明，对称矩阵，加入有一个m*m的对称矩阵，特定的λ为λi，对应的特征向量为xi，则有下面的推导：

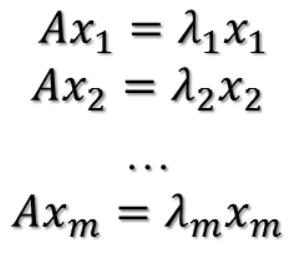
令U和Λ为：

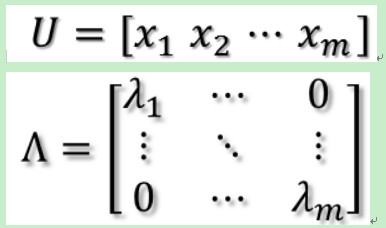
则有：

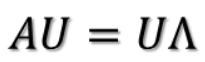
继续推导：

到此，注意Ax等式的右边是UT*x，这说明了什么，上大段我们讲述了旋转，U是一个正交矩阵，右乘了一个x，代表着要把x进行旋转，旋转到新的坐标轴下，旋转后的结果就是[a1, a2, a3...am]；于是有：

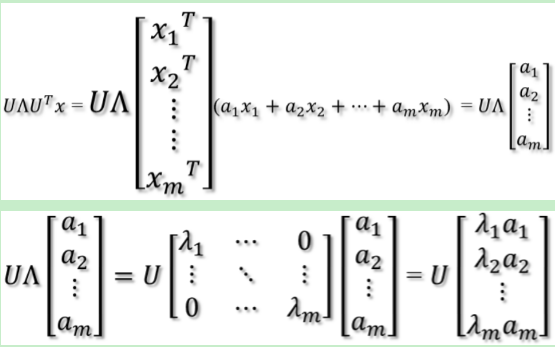
到了最后等到Ax的结果其实是对于原数据伸缩，完成这个的伸缩就是特征值 λi；然后U再左乘这个值，就实现了对于拉伸后数据的旋转。

 

 

 

参考：

向量的长度：

https://baike.baidu.com/item/%E5%90%91%E9%87%8F%E7%9A%84%E6%A8%A1/2073854?fr=aladdin

SVD原理：

https://blog.csdn.net/y1535766478/article/details/76944404