基本DFS与BFS算法（C++实现)

样图：

　　

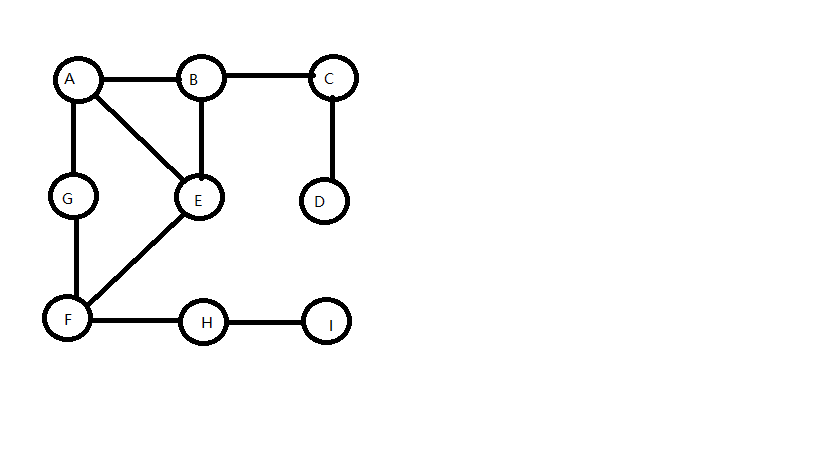
DFS:深度优先搜索，是一个不断探查和回溯的过程，每探查一步就将该步访问位置为true，接着在该点所有邻接节点中，找出尚未访问过的一个，将其作为下个探查的目标，接着对这个目标进行相同的操作，直到回到最初的节点，此时图中所有节点都访问过了。

BFS:广度优先搜索，是一个逐层遍历的过程，每探查一步就将该步访问位置为true，接着在该点所有邻接节点中，找出尚未访问过的一个，将其作为下个探查的目标，接着还是对该节点（而不是所选择的目标）剩下的未访问的点选择一个，作为下一个探查的目标，直到没有邻接点为止。这些探测过的点存放于一个队列中，当该节点没有邻接节点时，取出队首的点进行相同的操作，直到队列为空，此时图中所有节点都访问过了。

实现代码（邻接矩阵法和邻接表法）：

邻接矩阵法：(时间复杂度n^2)，n代表顶点

　

 #include<iostream>
 #include<queue>
 #define maxValue 100
 using namespace std;
 template<class E>
 class Graph{//图的邻接矩阵表示(无向图)
     public:
         Graph(int n){
             numV=n;
             vlist=new int[n];
             visited=new bool[n];
             edge=new E*[n];
             for(int i=;i<n;i++){
                 vlist[i]=i;
                 edge[i]=new E[n];
                 visited[i]=false;
             }
                 visited[]=true;
             for(int i=;i<n;i++){
                 for(int j=;j<n;j++){
                     edge[i][j]=(i==j)?:maxValue;
                 }
             }
         }
         ~Graph(){
             delete []vlist;
             delete []edge;
             delete []visited;
         }
         int getFirst(int v){//获取顶点V的第一个邻接点
             for(int col=;col<numV;col++)
                 if(edge[v][col]>&&edge[v][col]<maxValue)
                     return col;
             return -;
         }
         int getNext(int v,int w){//获取顶点V的某个邻接点w的下一个 邻接点
             for(int col=w+;col<numV;col++)
                 if(edge[v][col]>&&edge[v][col]<maxValue)
                     return col;
             return -;
         }
         bool removeV(int v){//删除一个定点上的所有关联边
             for(int i=;i<numV;i++){
                 if(i!=v){
                     edge[v][i]=maxValue;
                     edge[i][v]=maxValue;
                 }
             }
         }
         bool insertE(int v1,int v2,E cost){//插入边V1，V2
             edge[v1][v2]=edge[v2][v1]=cost;
         }
         bool removeE(int v1,int v2){//删除边V1，V2
             edge[v1][v2]=edge[v2][v1]=maxValue;
         }
         E getW(int v1,int v2){//返回边(v1,v2)上的权值
             return edge[v1][v2];
         }
         void DFS(int v){//深度优先搜索
             cout<<(char)(vlist[v]+)<<" ";//打印节点
             visited[v]=true;//标记该节点被访问过
             int w=getFirst(v);//w为节点v的第一个邻接节点
             while(w!=-){//v仍有临接节点未访问完
                 if(visited[w]==false) DFS(w);//如果w未被访问，对w进行新一轮DFS
                 w=getNext(v,w);//w重新设置成v的下一个临接节点
             }
         }
         void BFS(int v){//广度优先搜索
             cout<<(char)(vlist[v]+)<<" ";//打印节点
             visited[v]=true;//标记该节点被访问过
             queue<int> q;//辅助队列q
             q.push(v);//将节点v入队
             while(!q.empty()){//队列不为空
                 int v=q.front();//v为队首元素
                 q.pop();//v出队
                 int w=getFirst(v);//w为节点v的第一个邻接节点
                 while(w!=-){//v仍有临接节点未访问完
                     if(visited[w]==false){//如果w未被访问，打印节点， 标记该节点被访问过 ，并将该节点入队
                         cout<<(char)(vlist[w]+)<<" ";
                         visited[w]=true;
                         q.push(w);
                     }
                     w=getNext(v,w);//w重新设置成v的下一个临接节点
                 }
             }
         }
         void print(){//打印图
             for(int i=;i<numV;i++){
                 for(int j=;j<numV;j++){
                     if(edge[i][j]==maxValue)
                         cout<<"#"<<" ";
                     else
                         cout<<edge[i][j]<<" ";
                 }
             cout<<endl;
             }
         }
     private:
         int *vlist;
         bool *visited;
         E **edge;
         int numV;

 };
 //1-9分别对应A-I
 int main(){
     Graph<int> *g=new Graph<int>();
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
 //    g->DFS(1);//利用注释来回切换
     g->BFS();
     delete g;
     return ;
 }

邻接表法：(时间复杂度n+e),e代表边

 #include<iostream>
 #include<queue>
 #define maxValue 100
 using namespace std;
 template<class E>
 struct e{
     int v;
     e<E> *link;
     E cost;
     e(int _v,E w,e *l=NULL){
         v=_v;
         cost=w;
         link=l;
     }
 };
 template<class E>
 struct V{
     char data;
     e<E> *link;
     V(char d,e<E> *l=NULL){
         data=d;
         link=l;
     }
 };
 template<class E>
 class Graph{
     public:
         Graph(int n){
             numV=n;
             vlist=new V<E>*[n];
             visited=new bool[n];
             for(int i=;i<n;i++){
                 vlist[i]=new V<E>(i+);
                 visited[i]=false;
             }
             visited[]=true;
         }
         ~Graph(){
             delete[] vlist;
         }
         int getFirst(int v){
             e<E> *p=vlist[v]->link;
             if(p!=NULL)
                 return p->v;
             return -;
         }
         int getNext(int v,int w){
             e<E> *p=vlist[v]->link;
             while(p!=NULL&&p->v!=w){
                 p=p->link;
             }
             if(p!=NULL&&p->link!=NULL){
                 return p->link->v;
             }
             return -;
         }
         E getW(int v1,int v2){
             e<E> *p=vlist[v1]->link;
             while(p!=NULL&&p->v!=v2){
                 p=p->link;
             }
             if(p!=NULL){
                 return p->cost;
             }
             return ;
         }
         bool removeV(int v){
             e<E> *p,*q;
             int k;
             while(vlist[v]->link!=NULL){
                 e<E> *m=NULL;
                 p=vlist[v]->link;
                 k=p->v;
                 q=vlist[k]->link;
                 while(q!=NULL&&q->v!=v){
                     m=q;q=q->link;
                 }
                 if(q!=NULL){
                     if(m==NULL) vlist[k]->link=q->link;
                     else m->link=q->link;
                     delete q;
                 }
                 vlist[v]->link=p->link;
                 delete p;
             }
             return true;
         }
         bool insertE(int v1,int v2,int w){
             e<E> *p=vlist[v1]->link;
             e<E> *q;
             bool isIn=false;
             while(p!=NULL){
                 if(p->v==v2){
                     p->cost=w;
                     isIn=true;
                     break;
                 }
                     p=p->link;
             }
             if(isIn){
                 q=vlist[v2]->link;
                 while(q!=NULL){
                     if(q->v==v1){
                         q->cost=w;
                         break;
                     }
                     q=q->link;
                 }
                 return true;
             }else{
                 p=new e<E>(v2,w,vlist[v1]->link);
                 vlist[v1]->link=p;
                 q=new e<E>(v1,w,vlist[v2]->link);
                 vlist[v2]->link=q;
                 return true;
             }
             return false;
         }
         bool removeE(int v1,int v2){
             e<E> *p=vlist[v1]->link;
             e<E> *q=NULL;
             while(p!=NULL){
                 if(p->v==v2)
                     break;
                 else{
                     q=p;
                     p=p->link;
                 }
             }
             if(p!=NULL){
                 if(p==vlist[v1]->link) vlist[v1]->link=p->link;
                 else{
                     q->link=p->link;
                     delete p;
                 }
             }else{
                 return false;
             }
             p=vlist[v2]->link;
             q=NULL;
             while(p!=NULL){
                 if(p->v==v1)
                     break;
                 else{
                     q=p;
                     p=p->link;
                 }
             }
             if(p!=NULL){
                 if(p==vlist[v2]->link) vlist[v2]->link=p->link;
                 else{
                     q->link=p->link;
                     delete p;
                 }
             }else{
                 return false;
             }
         }
         void DFS(int v){
             cout<<vlist[v]->data<<" ";
             visited[v]=true;
             int w=getFirst(v);
             while(w!=-){
                 if(visited[w]==false) DFS(w);
                 w=getNext(v,w);
             }
         }
         void BFS(int v){
             cout<<vlist[v]->data<<" ";
             visited[v]=true;
             queue<int> q;
             q.push(v);
             while(!q.empty()){
                 int v=q.front();
                 q.pop();
                 int w=getFirst(v);
                 while(w!=-){
                     if(visited[w]==false){
                         cout<<vlist[w]->data<<" ";
                         visited[w]=true;
                         q.push(w);
                     }
                     w=getNext(v,w);
                 }
             }
         }
         void print(){//打印邻接表
             for(int i=;i<numV;i++){
                 cout<<vlist[i]->data<<"->";
                 e<E> *p=vlist[i]->link;
                 while(p!=NULL){
                     cout<<p->v<<" "<<p->cost<<"->";
                     p=p->link;
                 }
                 cout<<"^"<<endl;
             }
         }
     private:
          V<E> **vlist;
         bool *visited;
          int numV;
 };
 int main(){
     Graph<int> *g=new Graph<int>();
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
     g->insertE(,,);
 //    g->DFS(1);
     g->BFS();
     delete g;
     return ;
 }