洛谷P5280 [ZJOI2019]线段树 [线段树，DP]

传送门

---

无限Orz \(\color{black}S\color{red}{ooke}\)……

---

思路

显然我们不能按照题意来每次复制一遍，而多半是在一棵线段树上瞎搞。

然后我们可以从\(modify\)函数入手，寻找一些性质。

（盗一张Sooke的图）

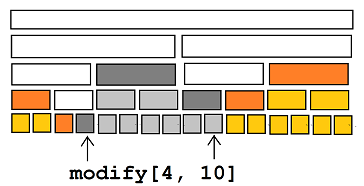
可以发现每次\(modify\)之中，所有节点都可以被分成5类：

1. 白色：经过而且标记全都被下传的点。
2. 黑色：打上标记的点。
3. 灰色：在修改区域内但不会被经过的点。
4. 橙色：可以享受到来自上方标记的滋润的点。
5. 黄色：半毛钱关系都没有的点……

分类之后，可以发现：如果DP的话，所有同一类型的点的转移方程都是基本相同的。

于是考虑DP：很自然地，想到设\(f_i\)表示在所有情况中\(tag_i=1\)的情况个数。

那么有转移方程：

\[f_i=\begin{cases}
f_i&,white\\
f_i+2^t&,black\\
2f_i&,grey\\
2f_i&,yellow\\
?????&,orange
\end{cases}
\]

你发现橙色点还要根据上方点是否有标记来转移，烦死了。

于是再一次很自然地，想到设\(g_i\)表示在所有情况中\(i\rightarrow root\)路径上存在\(tag_x=1\)的情况个数。

那么有转移方程：

\[g_i=\begin{cases}
g_i&,white\\
g_i+2^t&,black\\
g_i+2^t&,grey\\
2g_i&,yellow\\
2g_i&,orange
\end{cases}
\]

然后终于可以得到：

\[f_i=f_i+g_i,orange
\]

大功告成！

显然白色、黑色、橙色暴力转移，灰色、黄色随便维护下懒标记即可。

最后答案是\(\sum_i f_i\)，也是在线段树上很好统计的。

---

代码

#include<bits/stdc++.h>
clock_t t=clock();
namespace my_std{
    using namespace std;
    #define pii pair<int,int>
    #define fir first
    #define sec second
    #define MP make_pair
    #define rep(i,x,y) for (int i=(x);i<=(y);i++)
    #define drep(i,x,y) for (int i=(x);i>=(y);i--)
    #define go(x) for (int i=head[x];i;i=edge[i].nxt)
    #define templ template<typename T>
    #define sz 202020
    #define mod 998244353ll
    typedef long long ll;
    typedef double db;
    mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
    templ inline T rnd(T l,T r) {return uniform_int_distribution<T>(l,r)(rng);}
    templ inline bool chkmax(T &x,T y){return x<y?x=y,1:0;}
    templ inline bool chkmin(T &x,T y){return x>y?x=y,1:0;}
    templ inline void read(T& t)
    {
        t=0;char f=0,ch=getchar();double d=0.1;
        while(ch>'9'||ch<'0') f|=(ch=='-'),ch=getchar();
        while(ch<='9'&&ch>='0') t=t*10+ch-48,ch=getchar();
        if(ch=='.'){ch=getchar();while(ch<='9'&&ch>='0') t+=d*(ch^48),d*=0.1,ch=getchar();}
        t=(f?-t:t);
    }
    template<typename T,typename... Args>inline void read(T& t,Args&... args){read(t); read(args...);}
    char __sr[1<<21],__z[20];int __C=-1,__zz=0;
    inline void Ot(){fwrite(__sr,1,__C+1,stdout),__C=-1;}
    inline void print(register int x)
    {
        if(__C>1<<20)Ot();if(x<0)__sr[++__C]='-',x=-x;
        while(__z[++__zz]=x%10+48,x/=10);
        while(__sr[++__C]=__z[__zz],--__zz);__sr[++__C]='\n';
    }
    void file()
    {
        #ifndef ONLINE_JUDGE
        freopen("a.in","r",stdin);
        #endif
    }
    inline void chktime()
    {
        #ifndef ONLINE_JUDGE
        cout<<(clock()-t)/1000.0<<'\n';
        #endif
    }
    #ifdef mod
    ll ksm(ll x,int y){ll ret=1;for (;y;y>>=1,x=x*x%mod) if (y&1) ret=ret*x%mod;return ret;}
    ll inv(ll x){return ksm(x,mod-2);}
    #else
    ll ksm(ll x,int y){ll ret=1;for (;y;y>>=1,x=x*x) if (y&1) ret=ret*x;return ret;}
    #endif
//	inline ll mul(ll a,ll b){ll d=(ll)(a*(double)b/mod+0.5);ll ret=a*b-d*mod;if (ret<0) ret+=mod;return ret;}
}
using namespace my_std;
int n,m;
ll pow2;
ll f[sz<<2],g[sz<<2],fMul[sz<<2],gAdd[sz<<2],gMul[sz<<2];
ll S[sz<<2];
#define ls k<<1
#define rs k<<1|1
#define lson ls,l,mid
#define rson rs,mid+1,r
void mulf(int k,ll w){(f[k]*=w)%=mod;(fMul[k]*=w)%=mod;(S[k]*=w)%=mod;}
void mulg(int k,ll w){(g[k]*=w)%=mod;(gMul[k]*=w)%=mod;(gAdd[k]*=w)%=mod;}
void addg(int k,ll w){(g[k]+=w)%=mod;(gAdd[k]+=w)%=mod;}
void pushdown(int k)
{
    mulg(ls,gMul[k]);mulg(rs,gMul[k]);gMul[k]=1;
    addg(ls,gAdd[k]);addg(rs,gAdd[k]);gAdd[k]=0;
    mulf(ls,fMul[k]);mulf(rs,fMul[k]);fMul[k]=1;
}
void pushup(int k){S[k]=(S[ls]+S[rs]+f[k])%mod;}
void modify1(int k,int l,int r,int x,int y) // white,black,grey
{
    pushdown(k);
    int mid=(l+r)>>1;
    if (x<=l&&r<=y) // black
    {
        (f[k]+=pow2)%=mod;
        (g[k]+=pow2)%=mod;
        addg(ls,pow2);addg(rs,pow2); // grey
        mulf(ls,2);mulf(rs,2); // grey
        pushup(k);
        return;
    }
    // white (do nothing)
    if (x<=mid) modify1(lson,x,y);
    if (y>mid) modify1(rson,x,y);
    pushup(k);
}
void modify2(int k,int l,int r,int x,int y) // orange,yellow
{
    pushdown(k);
    if (x<=l&&r<=y) // orange
    {
        (f[k]+=g[k])%=mod;(g[k]+=g[k])%=mod;
        mulg(ls,2);mulg(rs,2); // yellow
        mulf(ls,2);mulf(rs,2); // yellow
        pushup(k);
        return;
    }
    int mid=(l+r)>>1;
    if (x<=mid) modify2(lson,x,y);
    if (y>mid) modify2(rson,x,y);
    pushup(k);
}
void build(int k,int l,int r)
{
    f[k]=g[k]=0;
    fMul[k]=gMul[k]=1;gAdd[k]=0;
    if (l==r) return;
    int mid=(l+r)>>1;
    build(lson);build(rson);
}
int main()
{
    file();
    read(n,m);
    build(1,1,n);
    int z,x,y;
    pow2=1;
    while (m--)
    {
        read(z);
        if (z==2) printf("%lld\n",S[1]);
        else
        {
            read(x,y);
            modify1(1,1,n,x,y);
            if (x!=1) modify2(1,1,n,1,x-1);
            if (y!=n) modify2(1,1,n,y+1,n);
            (pow2*=2)%=mod;
        }
    }
    return 0;
}