【洛谷】1852：[国家集训队]跳跳棋【LCA】【倍增？】

P1852 [国家集训队]跳跳棋

题目背景

原《奇怪的字符串》请前往 P2543

题目描述

跳跳棋是在一条数轴上进行的。棋子只能摆在整点上。每个点不能摆超过一个棋子。

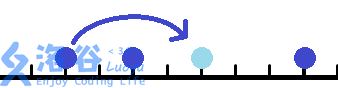
我们用跳跳棋来做一个简单的游戏：棋盘上有3颗棋子，分别在a，b，c这三个位置。我们要通过最少的跳动把他们的位置移动成x，y，z。（棋子是没有区别的）

跳动的规则很简单，任意选一颗棋子，对一颗中轴棋子跳动。跳动后两颗棋子距离不变。一次只允许跳过1颗棋子。

写一个程序，首先判断是否可以完成任务。如果可以，输出最少需要的跳动次数。

输入输出格式

输入格式：

第一行包含三个整数，表示当前棋子的位置a b c。（互不相同）

第二行包含三个整数，表示目标位置x y z。（互不相同）

输出格式：

如果无解，输出一行NO。

如果可以到达，第一行输出YES，第二行输出最少步数。

输入输出样例

输入样例#1： 复制

1 2 3
0 3 5

输出样例#1： 复制

YES
2

说明

20% 输入整数的绝对值均不超过10

40% 输入整数的绝对值均不超过10000

100% 绝对值不超过10^9

---

Solution

然而并不想写solution....

是一道建模题，谁能想到这道题和树可以扯上关系？？？？

把起点和终点状态拟成树上的两个节点，就像树上求链的长度一样找lca并且把两个节点到lca的距离加起来得到答案。

听起来好玄乎？？

更玄乎的是这种找lca的方法和倍增惊人地相似！

想要找到中间作为lca的转折状态，一步一步跳显然不行。由此观察题目本身的性质，给出的三个棋子是完全相同的，那么把一个作为中轴跳相当于把这两个棋子一起平移他们之间的距离。

这样可以快速地找到某一状态一直跳到不能跳时每个棋子的位置。所以首先判断如果给出的两个状态的最终状态不相同，那么输出‘NO’

所以我们还发现，两种状态跳到他们最终状态的步数的差就是它们‘深度’的差，就像倍增求lca先要把深度调成一样再一起往上跳。

所以先处理出以上需要的东西，有点像辗转相除？？每次都尽量跳到不能跳，然后交换继续跳。

将两个状态深度调到一样后，一起向上跳的步数就可以用二分，每次check往上跳看是否跳到一样。

二分出的答案要乘2（链）加上深度调到一样的答案即可。

Code

#include<bits/stdc++.h>
#define LL long long
using namespace std;

LL dep1, dep2, a, b, c, x, y, z, ans;

LL get_root(LL a, LL b, LL c, LL &dep, LL &l) {
    LL d1 = b - a, d2 = c - b;
    while(d1 != d2) {
        if(d2 > d1) {
            LL s = d2 / d1, dis = d2 % d1;
            if(!dis) {
                dep += s - ;
                l = d1;    return a + (s - ) * d1;
            }
            dep += s;    a += s * d1;    b += s * d1;
            d2 = dis;
        } else {
            LL s = d1 / d2, dis = d1 % d2;
            if(!dis) {
                dep += s - ;
                l = d2; return a;
            }
            dep += s;    b -= s * d2;    c -= s * d2;
            d1 = dis;
        }
    }
    dep = ;    l = d1;        return a;
} 

void Swap(LL &a, LL &b, LL &c) {
    if(a > b)    swap(a, b);
    if(a > c)    swap(a, c);
    if(b > c)    swap(b, c);
}

void find_fa(LL &a, LL &b, LL &c, LL step) {
    while(step) {
        LL d1 = b - a, d2 = c - b;
        if(d2 > d1) {
            LL s = d2 / d1;
            if(s >= step) {
                a += step * d1;    b += step * d1;
                return ;
            }
            a += s * d1;    b += s * d1;    step -= s;
        } else {
            LL s = d1 / d2;
            if(s >= step) {
                c -= step * d2;    b -= step * d2;
                return ;
            }
            c -= s * d2;    b -= s * d2;    step -= s;
        }
    }
}

void solve() {
    LL l = , r = min(dep2, dep1);
    LL st;
    while(l <= r) {
        LL mid = (l + r) >> ;
        LL aa = a, bb = b, cc = c;
        LL xx = x, yy = y, zz = z;
        find_fa(aa, bb, cc, mid);
        find_fa(xx, yy, zz, mid);
        if(aa == xx && bb == yy && cc == zz)    st = mid, r = mid - ;
        else    l = mid + ;
    }
    printf("%lld", ans + st * );
}

int main() {
    scanf("%lld%lld%lld%lld%lld%lld", &a, &b, &c, &x, &y, &z);
    Swap(a, b, c);    Swap(x, y, z);
    LL del1, del2;
    LL pos1 = get_root(a, b, c, dep1, del1);
    LL pos2 = get_root(x, y, z, dep2, del2);
    if(del1 != del2 || pos1 != pos2) {
        puts("NO");    return ;
    }
    puts("YES");
    if(dep1 > dep2) {
        ans += dep1 - dep2;
        find_fa(a, b, c, dep1 - dep2);
    } else if(dep2 > dep1) {
        ans += dep2 - dep1;
        find_fa(x, y, z, dep2 - dep1);
    }
    solve();
}