（来自百度百科）

1. 凹函数，不加权

2. 凹函数，加权

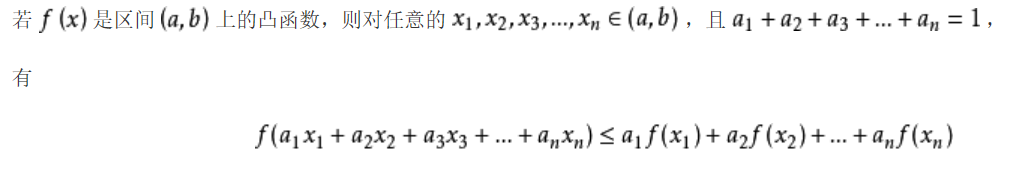
3. 凸函数，不加权

4. 凸函数，加权

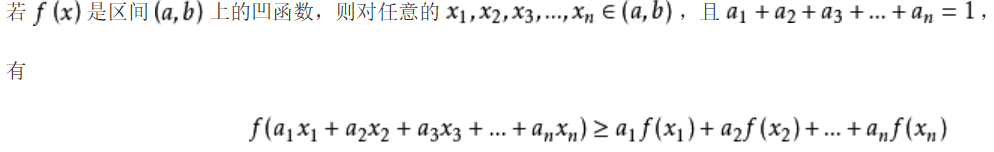
应用

在EM算法Q函数的推导中，用到了第二个不等式（凹函数，加权）

琴声不等式--jensen的更多相关文章

  1. 机器学习数学|微积分梯度jensen不等式

    机器学习中的数学 觉得有用的话,欢迎一起讨论相互学习~Follow Me 原创文章,如需转载请保留出处 本博客为七月在线邹博老师机器学习数学课程学习笔记 索引 微积分,梯度和Jensen不等式 Tay ...

  2. Expectation Maximization and GMM

    Jensen不等式 Jensen不等式给出了积分的凸函数值必定大于凸函数(convex)的积分值的定理.在凸函数曲线上的任意两点间连接一条线段,那么线段会位于曲线之上,这就是将Jensen不等式应用到 ...

  3. 【算法】CRF(条件随机场)

    CRF(条件随机场) 基本概念 场是什么 场就是一个联合概率分布.比如有3个变量,y1,y2,y3, 取值范围是{0,1}.联合概率分布就是{P(y2=0|y1=0,y3=0), P(y3=0|y1= ...

  4. cs229_part6

    part 6 接下来就是无监督学习算法了. k均值聚类 问题背景 样本集描述: \[ x\in D, x\in R^n \] 之前的有监督学习问题中,所有的x都有对应的y.但是如果我们的x没有对应的y ...

  5. 机器学习五 EM 算法

    目录 引言 经典示例 EM算法 GMM 推导 参考文献: 引言 Expectation maximization (EM) 算法是一种非常神奇而强大的算法. EM算法于 1977年 由Dempster ...

  6. 数学分析中jensen不等式由浅入深进行教学（转）

    中国知网:数学分析中Jensen不等式由浅入深进行教学

  7. Jensen 不等式

    若f(x)为区间I上的下凸(上凸)函数,则对于任意xi∈I和满足∑λi=1的λi>0(i=1,2,...,n),成立: \[f(\sum ^{n} _{i=1} \lambda _{i}x_{i ...

  8. 归并排序、jensen不等式、非线性、深度学习

    前言 在此记录一些不太成熟的思考,希望对各位看官有所启发. 从题目可以看出来这篇文章的主题很杂,这篇文章中我主要讨论的是深度学习为什么要"深"这个问题.先给出结论吧:"深 ...

  9. 【数学基础篇】---详解极限与微分学与Jensen 不等式

    一.前述 数学基础知识对机器学习还有深度学习的知识点理解尤为重要,本节主要讲解极限等相关知识. 二.极限 1.例子 当 x 趋于 0 的时候,sin(x) 与 tan(x) 都趋于 0. 但是哪一个趋 ...

随机推荐

  1. Linux - 搭建FastDFS分布式文件系统

    1. FastDFS简介 说明:FastDFS简介部分的理论知识全部来自于博主bojiangzhou的 <用FastDFS一步步搭建文件管理系统>,在此感谢博主的无私分享.当然最最要感谢的 ...

  2. sqlmap参数

    sqlmap -u “http://url/news?id=1" –current-user #获取当前用户名称sqlmap -u “http://www.xxoo.com/news?id= ...

  3. python获取网站http://www.weather.com.cn 城市 8-15天天气

    参考一个前辈的代码,修改了一个案例开始学习beautifulsoup做爬虫获取天气信息,前辈获取的是7日内天气, 我看旁边还有8-15日就模仿修改了下.其实其他都没有变化,只变换了获取标签的部分.但是 ...

  4. NYOJ 44 字串和 （最大字串和 线性dp）

    题目链接: http://acm.nyist.edu.cn/JudgeOnline/problem.php?pid=44 子串和 时间限制:5000 ms  |  内存限制:65535 KB 难度:3 ...

  5. 404 Note Found队Beta3

    目录 组员情况 组员1(组长):胡绪佩 组员2:胡青元 组员3:庄卉 组员4:家灿 组员5:凯琳 组员6:翟丹丹 组员7:何家伟 组员8:政演 组员9:黄鸿杰 组员10:刘一好 组员11:何宇恒 展示 ...

  6. MongoDB初学笔记(1)

    学习目标 理解MongoDb的特点和体系结构 掌握常用的MongoDB命令 MongoDB是一种介于关系数据库和非关系数据库中的一种数据库.它支持的数据结构非常松散,类似于JSON的BJSOn格式,所 ...

  7. HTTP协议图

  8. 20154327 Exp9 Web安全基础

    基础问题回答 (1)SQL注入攻击原理,如何防御 原理: 程序员在编写代码的时候,没有对用户输入数据的合法性进行判断,攻击者利用SQL命令欺骗服务器执行恶意的SQL命令,获得某些他想得知的数据. 防御 ...

  9. 【HNOI2013】比赛

    题面 题解 \(n \leq 9 \to\)爆搜 对每一场的结果进行搜索,最后进行\(\mathrm{check}\) 然后会发现没有什么分 搜索最重要的就是剪枝 接下来就列出一些剪枝 搜索时,强制每 ...

  10. cmp(x,y)

    cmp(x,y) 函数用于比较2个对象,如果 x < y 返回 -1, 如果 x == y 返回 0, 如果 x > y 返回 1.