回归算法
以下均为自己看视频做的笔记,自用,侵删!
一、线性回归

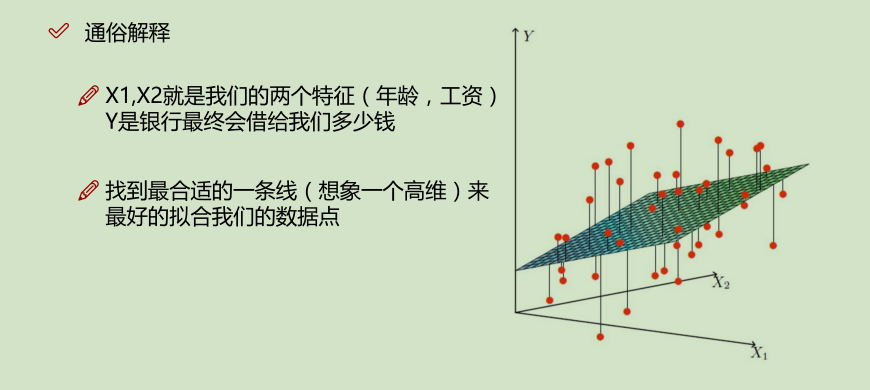
θ是bias(偏置项)




线性回归算法代码实现
# coding: utf-8
get_ipython().run_line_magic('matplotlib', 'inline')
import matplotlib.pylab as plt
import numpy as np
from sklearn import datasets
# $h_{\theta}(x)=\theta_0+\theta_1x_1+\theta_2x_2$
#
# 将 $\theta_0$ 放到权重项上来,将 $\theta_0$ = 1
class LinearRegression():
def __init__(self):
self.w = None
def fit(self, X, y):
# Insert constant ones for bias weights
print("first:", X.shape)
# 在第0项,插入 1,让x0项为1
X = np.insert(X, 0, 1, axis=1)
print("second:", X.shape)
# inv(): 对当前值取逆, dot():矩阵计算
X_ = np.linalg.inv(X.T.dot(X))
# 算出来 最好的 一组参数 theta
self.w = X_.dot(X.T).dot(y)
def predict(self, X):
# Insert constant ones for bias weights
X = np.insert(X, 0, 1, axis=1)
y_pred = X.dot(self.w)
return y_pred
def mean_squared_error(y_true, y_pred):
mse = np.mean(np.power(y_true - y_pred, 2))
return mse
def main():
# load the diabetes dataset
diabetes = datasets.load_diabetes()
# Use only one feature
X = diabetes.data[: , np.newaxis, 2]
print(X.shape)
# split the data into training/testing sets
x_train, x_test = X[:-20], X[-20:]
# Split the targets into training/testing sets
y_train, y_test = diabetes.target[:-20], diabetes.target[-20:]
clf = LinearRegression()
clf.fit(x_train, y_train)
y_pred = clf.predict(x_test)
# Print the mean squared error
print("Mean Squared Error:", mean_squared_error(y_test, y_pred))
# Plot the results
plt.scatter(x_test[: , 0], y_test, color='black')
plt.plot(x_test[:, 0], y_pred, color="blue", linewidth=3)
plt.show()
main()
(442, 1)
first: (422, 1)
second: (422, 2)
Mean Squared Error: 2548.07239873
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAhMAAAFdCAYAAAC5Ge+lAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz%0AAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBo%0AdHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzt3Xt4ZWV96PHvjwhTRGakyiXOHo0W%0Ar6BiEbnU4ESFo6KiMU/VUby3ah97Mt4PPVXRXmwR7cRLFamnWhQPNu4jgiLITVNBFESBI2KPHXQm%0AExhwYAa5DBLe88dam+zZszOTtS/Jvnw/z7OeTNZ637XflZXJ/u3fe1mRUkKSJKlReyx1AyRJUncz%0AmJAkSU0xmJAkSU0xmJAkSU0xmJAkSU0xmJAkSU0xmJAkSU0xmJAkSU0xmJAkSU0xmJAkSU0xmJAk%0ASU15yFI3oBEREcCjgDuXui2SJHWhfYFNqUUP6OrKYIIskNi41I2QJKmLlYDpVpyoW4OJOwE2bNjA%0A8uXLl7otkiR1jW3btrFq1SpoYXa/W4MJAJYvX24wIUnSEnMApiRJaorBhCRJaorBhCRJaorBhCRJ%0AaorBhCRJaorBhCRJakpXTw2VJKmTzc7OMjU1xczMDIODgwwPDzMwMLDUzWo5gwlJktqgXC4zPj7O%0Axo1zCzaXSiUmJiYYHR1dwpa1nt0ckiS1WLlcZmxsbIdAAmB6epqxsTHK5fIStaw9okXP+FhUEbEc%0A2Lp161ZXwJQkdZTZ2VmGhoZ2CiQqIoJSqcT69euXpMtj27ZtrFixAmBFSmlbK85pZkKSpBaampqa%0AN5AASCmxYcMGpqamFrFV7WUwIUlSC83MzLS0XDcwmJAkqYUGBwdbWq4bGExIktRCw8PDlEolIqLu%0A8Yhg1apVDA8PL3LL2sdgQpKkFhoYGGBiYgJgp4Ci8v26det6ar0JgwlJklpsdHSUyclJVq5cucP+%0AUqnE5ORkz60z4dRQSZLapBNXwFzyqaER8faIuDYituXbFRHxwqrjyyLiUxFxW0TcFRHfjIhSzTke%0AHRHn5sdvi4hPRsRerbgYSZI6ycDAAKtXr+bVr341q1evXvJAol2KdnNsBP4H8Mx8uwQ4JyIOyY+v%0AA14OvAp4NvAw4LyIGADIv34L2Cc//irgFcDHm7sMSZK0VJru5oiILcB7gUngVuCklNLZ+bFHARuA%0AF6WULsizGOcBq1JKm/IyrwK+CByw0HSL3RySJDVmybs5qkXEQB4I7ANcARwO7AlcWCmTBwzXA8fk%0Au44Grq8EErkLgGV5/flea1lELK9swL6NtluSJLVW4WAiIp4aEb8DtgOfA16eUvo5cBBwX0rp9poq%0At+THyL/eUn0wL39fVZl6Tga2Vm3zr1MqSZIWVSOZiRuBw4CjgM8CX4qIp+yifADVfSn1+lVqy9T6%0AKLCiaivtoqwkSVpEDylaIaV0H/D/8m+viogjgHHgbGCviNivJjtxAHB5/u+bgSOrzxcR+5F1j+yQ%0Asah5ze1kmZBKnaLNliRJbdKKRauCbMzD1cDvgeMePBAxCBzKXDBxBXBovr/ieLJA4eoWtEWSJC2y%0AQpmJiPh74HyyGRr7kk3tXA28IKW0NSK+AHw8In4LbAFOA64DLspPcSHwc+DMiHgv8Id5mTNaNaJU%0AkiQtrqLdHAcCZwKDZAMhryULJL6bH38ncD/wNWBv4GLgDSmlWYCU0mxEnAD8M/AD4B7gLOA9TV6H%0AJElaIi6nLUlSH+modSYkSZLAYEKSJDXJYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKS%0AJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXF%0AYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKS%0AJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXF%0AYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDXFYEKSJDWlUDARESdHxI8j4s6I2BwR34iIJ9aU%0AuSwiUs32v2vK7BcRZ0bE1nw7MyIe3ooLkiRJi6toZuI5wGeAo4DjgIcAF0bEPjXlzgAGq7a31hw/%0ACzgMeEG+HQacWbAtkiSpAzykSOGU0guqv4+INwKbgcOB71cdujuldHO9c0TEk8kCiKNSSlfm+/4M%0AuCIinphSurFImyRJ0tJqdszEivzrlpr9r4mI2yLi/0bEaRGxb9Wxo4GtlUACIKX0Q2ArcEy9F4mI%0AZRGxvLIB+9YrJ0mSFl+hzES1iAjgE8B/pJSurzr0FWA9cDNwKPBR4Olk3SIAB5FlM2ptzo/VczLw%0AoUbbKkmS2qfhYAL4NPA04NnVO1NKZ1R9e31E/CdwVUT8cUrpJ5Vidc4X8+yHLCD5RNX3+wIbG2q1%0AJElqqYaCiYj4FPBS4NiU0u7e1H8C/B54fP7vm4ED65TbH7il3glSStuB7VWv30CrJUlSOxSdGhoR%0A8WlgFHhuSmn9AqodAuwJzOTfXwGsiIhnVZ33SLLxF5cXaY8kSVp6RTMTnwHWACcCd0ZEZYzD1pTS%0APRHxR8BrgG8DtwFPAT4OXAP8ACCldENEfAc4IyIqU0Y/D5znTA5JkrpP0dkcbyfLIFxGlmmobK/M%0Aj98HPA+4ALgR+CRwIfD8lNJs1XleA1yXH7sQuBY4qaErkCRJS6roOhO7HKyQUtpAtrDV7s6zBXht%0AkdeWJEmdyWdzSJKkphhMSJKkphhMSJKkphhMSJKkphhMSJKkphhMSJLUBlu3wktfChEwPr7UrWmv%0AZp7NIUlSV5qdnWVqaoqZmRkGBwcZHh5mYGCgJee+4AJ4wQt23PfJT8L27fC5z7XkJTqOmQlJUl8p%0Al8sMDQ0xMjLCmjVrGBkZYWhoiHK53PA5770XXv/6LAtRG0hUnH56w6fveAYTkqS+US6XGRsbY+PG%0AHZ9ROT09zdjYWOGA4kc/gj32gL33hn/7t12Xfe97i7a2exhMSJL6wuzsLOPj46SUdjpW2bd27Vpm%0AZ2d3Or7jebLAIAKOPBLqnG4nH/wgnHpqQ83uCo6ZkCT1hampqZ0yEtVSSmzYsIGpqSlWr1690/Eb%0Ab4Rjj4XNmxf+mt/8JrzkJQ00tsuYmZAk9YWZmZnC5VKCj30sy0I86UkLCySe9zz47W+zuv0QSICZ%0ACUlSnxgcHFxwuenpbCDl9dcv/Pz/+q/whjc01rZuZzAhSeoLw8PDlEolpqen646biAj2228tIyOr%0AF3zOQw+F88+HUqmFDe1CdnNIkvrCwMAAExMTQBY4zHk4cBEpPcCWLZ9Y0LlOPRUeeACuu85AAgwm%0AJEl9ZHR0lMnJSVauXAm8E0jA7cDzdlv3wAPhhhuysRCV2RzKRL1UT6eLiOXA1q1bt7J8+fKlbo4k%0AqUts2waPeATcf//C67znPfAP/wAtWiBzyW3bto0VK1YArEgpbWvFOc1MSJJ63tlnZ5mEFSsWFkhE%0AwJVXzs3m6JVAol0MJiRJPWn7dnj847PA4FWvWlid178e7rknGw/xrGe1t329xNkckrSE2vnAqX51%0A6aXw3OcWq3PmmfDa17anPf3AYEKSlki5XGZ8fHyHVRlLpRITExOMjo4uYcu6zwMPwAtfCBdeWKze%0ALbfAAQe0p039xG4OSVoCrX7gVL+69tqsG2NgYOGBxMknZ2MhUjKQaBVnc0jSIpudnWVoaGje50RE%0ABKVSifXr19vlMY+3va34I73/8z/h4IPb055u4mwOSeoBRR44pTm/+U2WhYhYeCCxZk3WBZKSgUQ7%0AGUxI0iJr5IFT/ezv/z4LIB7zmIXX+dGPsgDiK19xcanF4ABMSVpkRR441a+2bMkWlyrimGPg+993%0ATYilYGZCkhZZ5YFTMc9H5ohg1apVDA8PL3LLlt6XvpRlEooEEt/6VpaF+MEPDCSWisGEJC2y+R84%0ANff9unXr+mbw5T33wMqVWRCx0Ed4Dw7C3XdnQcSLXtTW5mkBDCYkaQns+MCpOaVSicnJyb5YZ+I7%0A38kCiIc+FDZtWlidL3whCyA2bYK9925v+7RwTg2VpCXUbytgzs7Cc56TdUkUcdttxcdQqL52TA11%0AAKYkLaGBgQFWr1691M1ou6uugiOOKFbnIx+BD3ygPe1RaxlMSJLaIiU46aRsemYRN91UbBqolp5j%0AJiRJLfWrX2VjIfbYY+GBxJvfPLfEtYFE9zGYkCS1xF//dRZEFFlp8pprsgDiX/6lfe1S+9nNIUlq%0A2K23Fn9Y1vOelz2Uaw8/zvYMb6UkqbDTT8+yEEUCiYsuyrIQF11kINFrzExIkhbkrrugVII77lh4%0Ancc9Dn7+c1i2rH3t0tIzNpQk7dI552RZiIc9bOGBxFe+kmUhfvUrA4l+YGZCkrST++4rHgTssUf2%0AgK5sPST1EzMTkqQHVR60VSSQOPXULAsxO2sg0a/MTEhSn0upsQGRGzdmD+iSCv36RMTJEfHjiLgz%0AIjZHxDci4ok1ZZZFxKci4raIuCsivhkRpZoyj46Ic/Pjt0XEJyNir1ZckCRpYS69dG5xqYV6xzvm%0AFpcykFBF0czEc4DPAD/O6/4dcGFEPCWldFdeZh3wEuBVwG+BjwPnRcThKaXZiBgAvgXcCjwbeATw%0AJSCAv2zyeiRJu3HAAdn6EEVccw0cdlh72qPu19RTQyNif2Az8JyU0vcjYgVZkHBSSunsvMyjgA3A%0Ai1JKF0TEC4HzgFUppU15mVcBXwQOWMgTzHxqqCQVc8MN8JSnFK83O+uaEL2mHU8NbfZXpDLUZkv+%0A9XBgT+DCSoE8YLgeOCbfdTRwfSWQyF0ALMvr7yTvOlle2YB9m2y3JPWF44/PujKKBBKnnz7XlWEg%0AoYVoeABmRATwCeA/UkrX57sPAu5LKd1eU/yW/FilzC3VB1NKt0fEfVVlap0MfKjRtkpSP9m8GQ48%0AsHi9e+6BP/iD1rdHva+ZmPPTwNOAVy+gbADV/Sn1+lZqy1T7KFkWpLKV5iknSX3rXe/KshBFAon3%0AvW8uC2EgoUY1lJmIiE8BLwWOTSltrDp0M7BXROxXk504ALi8qsyRNefbj6x7ZIeMRUVKaTuwvap8%0AI82WpJ5z992wzz7F623eDPvv3/r2qD8VnRoaEfFpYBR4bkppfU2Rq4HfA8dV1RkEDmUumLgCODTf%0AX3E8WbBwdbHmS1J/+uxnsyxEkUDixS+ey0IYSKiVimYmPgOsAU4E7oyIyhiHrSmle1JKWyPiC8DH%0AI+K3ZAMzTwOuAy7Ky14I/Bw4MyLeC/xhXuaMVo0qlaRe9MADMDBQvN4vfgFPfOLuy0mNKjpm4u1k%0AYxYuA2aqtldWlXkn8A3ga8APgLuBl6SUZgHyrycA9+bHv5aXf0+jFyFJvezb386yEEUCiVJpLgth%0AIKF2a2qdiaXiOhOS+sFee8Hvf1+szve+B8ce2572qDe0Y50Jn80hSR3kpz+FZzyjeL0HHsiyF9JS%0AcDkSSeoARx6ZBQNFAokvf3muK8NAQkvJzIQkLZFf/rKx8Qzbt2ddIFKnMDMhSYvsCU/IMglFAokP%0Af3guC2EgoU5jZkKSFsGWLfCIRxSvd/vt8PCHt749UiuZmZCkNjrppCwLUSSQePWr57IQBhLqBmYm%0A+sTs7CxTU1PMzMwwODjI8PAwA42sfiNpt37/+8a6IlxcSt3KzEQfKJfLDA0NMTIywpo1axgZGWFo%0AaIhyubzUTZN6ymmnZVmIooGEi0up27loVY8rl8uMjY1Re58rD0ubnJxkdHR0KZom9YSUYI8GPpad%0Adx6ccELr2yPtTjsWrTKY6GGzs7MMDQ2xcePGuscjglKpxPr16+3ykAo691x46UuL1+vCP7nqMe0I%0AJuzm6GFTU1PzBhIAKSU2bNjA1NTUIrZK6m4R2VYkkPj4x+e6MqRe5ADMHjYzM9PSclIna+cg42uv%0Ahac/vXi9++6DPfdsSROkjmZmoocNDg62tJzUqdo1yPiRj8yyEEUCide9bi4LYSChfuGYiR5WGTMx%0APT290wBMcMyEekOrBxnfcgscdFDxdmzZAvvtV7yetNgcM6FCBgYGmJiYAOb+sFZUvl+3bp2BhLrW%0A7Ows4+PjdYPlyr61a9cyOzu723O95CVZFqJIIPGkJ81lIQwk1M8MJnrc6Ogok5OTrFy5cof9pVLJ%0AaaHqes0OMr733rkBleedt/DX/eUvswDihhuKtljqTQ7A7AOjo6OceOKJroCpntPoIOMPfhD+5m+K%0Av14X9gpLi8Jgok8MDAywevXqpW6G1FJFBhk3urjUxRfDc59bvF4vcBl+LZTBhKSuNTw8TKlU2uUg%0A4/32+wtGRlYXPne/ZyHK5TLj4+M7dCOVSiUmJibsHtVOHDMhqWvtapAxJFJ6gC1bPr3g851+uotL%0AwdwMmdrxKNPT04yNjflcH+3EqaGSut7cp+iVwA8L17//fjB7n3EZ/t7n1FBJquMVrxhl48YNFAkk%0A/vt/n8tC+J44x2X41QjHTEjqSr/8ZWOP7N62Dfbdt/Xt6RUuw69GmJmQ1FUe8pBsXYgigcQxx8xl%0AIQwkds1l+NUIgwlJHe+OO+YWl1rAYpYP+vWvswDiBz9oX9t6TWWGzM4DWjMRwapVqxgeHl7klqmT%0AGUxI6ljHH58FEEWXqq5kIR796Pa0q5e5DL8aYTAhqaPMzs5lIb773YXXO/98p3W2isvwqyinhkrq%0ACC5x3XlcAbM3tWNqqLM5JC2pebrmd+m00+Dd7259W7Qjl+HXQhlMSFp0n/88vPWtxes98EBjwYek%0A9jKYkLRoGgkE/vRP4eyzW98WSa1jMCGprS6/HP7kT4rX+93vYJ99Wt8eSa1nMCGpLRrJQhx4INx8%0Ac+vbIqm9nBoqqWU2bZqb1lnETTdlszIMJKTuZGZCUtP23DN78mZRTuuUeoOZCUkN2b59LgtRJJA4%0A7zwXl5J6jZkJSYW89KVw7rnF6xk8SL3LzISk3UppLgtRJJD42781CyH1AzMTkuZ16qnw/vcXr+fi%0AUlJ/MZjQknP9/87TSCBw3HFw4YWtb4ukzmc3h5ZUuVxmaGiIkZER1qxZw8jICENDQ5TL5aVuWt/5%0A+tcbm9Z5991ZN4aBhNS/CgcTEXFsRJwbEZsiIkXEy2qOfzHfX739sKbMsoj4VETcFhF3RcQ3I6LU%0A7MWou5TLZcbGxti4ceMO+6enpxkbGzOgWCSVAGJsrFi9yliIvfduT7skdY9GMhP7AD8D3rGLMt8B%0ABqu2F9UcXwe8HHgV8GzgYcB5EWFuu0/Mzs4yPj5OqjMyr7Jv7dq1zM7OLnbT+sINNzSWhfjNbxxQ%0AKWlnhcdMpJTOB84HiPn/Em1PKdVdyy4iVgBvBk5KKV2U73stsAF4PnBB0Tap+0xNTe2UkaiWUmLD%0Ahg1MTU35COQWanRQpMGDpF1p15iJ1RGxOSJ+GRFnRMQBVccOB/YEHuxhTSltAq4HjmlTe9RhZmZm%0AWlpO89u2rbEsxLe/bRZC0sK0YzbH+cC/A78GHgv8DXBJRByeUtoOHATcl1K6vabeLfmxnUTEMmBZ%0A1a59W95qLarBwcGWltPOHvlI+O1vi9czeJBUVMszEymls1NK30opXZ9SOhd4IfAE4ITdVA1gvj9j%0AJwNbq7b58+PqCsPDw5RKpXm7yiKCVatWMTw8vMgt627Vi0sVCSQ+/GGzEJIa1/apoSmlGbIsxePz%0AXTcDe0XEfjVFDyDLTtTzUWBF1ebMjy43MDDAxMQEsPPYm8r369atc72JBXrDG7IAYo+C/6MrAcQH%0AP9iWZknqE20PJiLiEcAqoNL5fTXwe+C4qjKDwKHA5fXOkVLanlLaVtmAO9vbai2G0dFRJicnWbly%0A5Q77S6USk5OTjI6OLlHLukclC/GlLy28zrOfbRZCUmtFval5u6wQ8TDg4Pzba4B3AZcCW/LtFODr%0AZMHDEPD3wKOBJ6eU7szP8VngxcAb8jqnAY8ADk8p7XYuYEQsB7Zu3bqV5cuXF2q/Oo8rYBbzhS/A%0AW95SvN5992WPCpfU37Zt28aKFSsAVuQf0JvWyADMZ5IFDxWfyL9+CXg78FTgdcDDyQKKS4FXVgKJ%0A3DuB+4GvAXsDFwNvWEggod4zMDDg9M8FcFqnpE5VODPRCcxMqF9cdRUccUTxeps2gRNhJNXTKZkJ%0ASW1mFkJSN/FBX1KHuPXWxhaXmppyQKWkpWVmQlpiZiEkdTszE9ISuP/+xrIQn/ykWQhJncfMhLSI%0A/vzP4YwzitczeJDUyQwmpEXQSFfGK14Bk5Otb4sktZrdHFKb/K//1VhXxv33Z5kIAwlJ3cLMhNRi%0AjWQh9twzW6FSkrqRmQmpBa68srEsxDnn/Af33z9rICGpqxlMSE2oBBBHHVW4JhCceOIwQ0NDlMvl%0ANrROkhaHwYRU0MxMY1mIiYkLidiDLJCYMz09zdjYmAGFpK7lszmkBXroQ+Gee4rXSyl7MurQ0BAb%0AN26sWyYiKJVKrF+/3iemSmqrdjybw8yEtAv33TeXhSgSSHzzmzsuLjU1NTVvIAGQUmLDhg1MTU01%0A2WJJWnzO5pDqGB2F//N/itebL9E3MzOzoPoLLSdJncTMhFSlkoUoEkh86EO7X+J6cIHPA19oOUnq%0AJAYT6nuf+ERjAyofeCALIE45Zfdlh4eHKZVKxDwvEhGsWrWK4eHhYo2QpA5gMKG+VQkg3v3uhdcZ%0AGZnLQhQJPgYGBpiYmMhfd8eKle/XrVvn4EtJXclgQn3loosay0LcdVcWQFxySeOvPTo6yuTkJCtX%0Artxhf6lUYnJyktHR0cZPLklLyKmh6guNLHEN7Xla5+zsLFNTU8zMzDA4OMjw8LAZCUmLph1TQ53N%0AoZ61fj087nHF6910EzzmMS1vzoMGBgZYvXp1+15AkhaZwYS6Xu0n/ZGR1Q2dpwuTdJLUEQwm1NXK%0A5TLj4+Ns3LgFuKtw/UsuyQZVSpIaZzChrlUul3nFKx4JbChc1yyEJLWOwYS6Tkqwxx4AxWY/rFsH%0A4+NtaZIk9TWnhqprfOAD2ayMPQr+1lbWhTCQkKT2MDOhjtfYtM6vAa/krLPOAl7d2gZJknZgZkId%0A6RvfaGxxKdgLCOCVgM+6kKTFYGZCHaWxLMRW4OE15wlKpZLPupCkRWBmQktuerqxLMQXvvAtIvYg%0AYr8d9vusC0laXAYTWjLPf34WQJRKxepVBlS+6U0n+KwLSeoAPptDi+ruu2GffYrX+9GP4Igj6h/z%0AWRfdx3smLR2fzaGu9b73wcc+VrzeQmJdn3XRXeZWLd344L5SqcTExITZJKlL2c2htnnggbmxEEUC%0AiXPOmevKUG8pl8uMjY3tEEgATE9PMzY2RrlcXqKWSWqG3RxquS9+Ed74xuL1uvBXUQXMzs4yNDS0%0AUyBRUZmBs379ers8pDZqRzeHmQm1TCULUSSQ+Nd/NQvRL6ampuYNJABSSmzYsIGpqalFbJWkVnDM%0AhJoyNQXHHlu83uxs8WWx1d1mZmZaWk5S5/DPuRpSyUIUCSTe8565LISBRP9Z6GqkrloqdR8zE1qw%0A//ov+KM/Kl7vd79rbDpor+rXaZHDw8OUSiWmp6epN1bLVUul7uXnQ+3WH/9xloUoEkiMjMxlIQwk%0A5pTLZYaGhhgZGWHNmjWMjIwwNDTUF7MYBgYGmJiYAOZWKa1w1VKpuxlMqK6tW+e6Mq65ZuH1Nm7M%0AAohLLmlf27qV0yJhdHTUVUulHuTUUO3grW+Fz3++WJ1ly+Dee9vTnl7htMgd9WtXj9QJXAFTbXH/%0A/bDnnsXr/fjH8Mxntr49vajItMh+WM3TVUul3lK4myMijo2IcyNiU0SkiHhZzfGIiFPy4/dExGUR%0AcUhNmf0i4syI2JpvZ0bEjs+QVtt9+tNZN0bRQKIyFsJAYuGcFimplzUyZmIf4GfAO+Y5/j7gXfnx%0AI4Cbge9GxL5VZc4CDgNekG+HAWc20BY1oDIW4i//cuF1/v3fXVyqGU6LlNTLmhozEREJeHlK6Rv5%0A9wFsAtallP4x37cMuAV4f0rp9Ih4MvBz4KiU0pV5maOAK4AnpZRuXMDrOmaioJ/8BA4/vHi9yvM1%0A1JzKmIndTYvslzETkpZONyyn/VjgIODCyo6U0nbge8Ax+a6jga2VQCIv80Nga1WZHUTEsohYXtmA%0AfeuV084OPzwLBooEEh/5yFwWwkCiNZwWKamXtTqYOCj/ekvN/luqjh0EbK5Td3NVmVonkwUblW3+%0AkWxiw4a5royf/GTh9e69NwsgPvCB9rWtnzktUlKvatdsjto8btTsq9e3Ulum2keBT1R9vy8GFDs5%0A5RT48IeL1Rkdha9/vS3NWXTdMN1wdHSUE088sePbKUlFtDqYuDn/ehBQPSz9AOayFTcDB9apuz87%0AZzSAB7tKtle+r00T97N77oGDD4ZNm4rV27wZ9t+/PW1aCuVymfHx8R2mX5ZKJSYmJjruE7/TIiX1%0AmlZ3c6wnCxaOq+yIiL2A5wCX57uuAFZExLOqyhwJrKgqo934zneyboyHPnThgcRrXjM3FqLXAol+%0AX1lSkpZS4dkcEfEw4OD822vIpoFeCmxJKf0mIt5PNsbhjcB/An8FrAaemFK6Mz/H+cCjgLfm5/k8%0A8OuU0ksW2Ia+nM0xOwvDw3DFFcXq3XQTPOYxbWlSyxXtqnBlSUkqplNmczyTLIioPLHhE/m/P5J/%0AfyqwDvhn4CpgJXB8JZDIvQa4jmzWx4XAtcBJDbSlL1x1VZaFeMhDFh5IPO1pc1mIbgkkGnkIVpGV%0AJSVJ7VF4zERK6TKywZLzHU/AKfk2X5ktwGuLvnY/SQle+1o466xi9davh6GhtjSprSpdFbWZskpX%0AxXyzHVxZUpKWnk8N7TC/+lWWhdhjj4UHEm9+81wWohsDidnZWcbHx+su5lTZt3btWmZnZ3c67sqS%0AkrT0DCY6xF//dRZEHHzw7stWXHNNFkD8y7+0r12LoZmuiuHhYUql0rwzfCKCVatWMTw83LL2SpJ2%0AZDCxhG69dW5xqb/7u4XVee5zs4GYKcFhh7W3fYulma4KV5aUpKVnMLEEPve5LIA44ICF1/nud7MA%0A4uKLsy6QXtJsV4UrS0rS0mronPVnAAAPLUlEQVTqQV9LpRunht51F5RKcMcdC6/z2MfCDTfAsmXt%0Aa1cnaNVDsLphBUxJWmrtmBraruW0lTvnHHjZy4rV+fKXswWm+kWlq2JsbIyI2CGgKNJV4cqSkrQ0%0Aeixh3hnuvx+e8YysK2OhgURElrVIqb8CiQq7KiSpe9nN0UKXXw5/8ifF6px6Krz3ve1pTzeyq0KS%0A2stujg517bXw9KcXq7NxI9R8CBd2VUhSN7Kbo0kPPLDwQOId75hbXMpAQpLUK8xMNOnyBTzn9Prr%0A4ZBD2t8WSZKWgpmJJs03RuLFL86yFikZSEiSepvBRJMiYNMmeMIT4Jhj4Gc/ywKIc8/NjkmS1Ovs%0A5miBwUG48calboUkSUvDzIQkSWqKwYQkSWqKwYQkSWqKYyZ6iKtHSpKWgsFEjyiXy4yPj7Nx48YH%0A95VKJSYmJnyuhSSprezm6AHlcpmxsbEdAgmA6elpxsbGKJfLS9QySVI/8EFfXW52dpahoaGdAomK%0AiKBUKrF+/Xq7PCRJbXnQl5mJLjc1NTVvIAGQUmLDhg1MTU0tYqskSf3EYKLLzczMtLScJElFOQCz%0Ayw0ODra0nFSUs4gkGUx0ueHhYUqlEtPT09Qb/1IZMzE8PLwEresMvtm1j7OIJIHdHF1vYGCAiYkJ%0AIAscqlW+X7duXd++eZbLZYaGhhgZGWHNmjWMjIwwNDTkDJcWcBaRpApnc/SIep8QV61axbp16/r2%0AE2Llza72d7wSZE1OThb62ZjhmOMsIql7tWM2h8FED/HNbk6r3+xM5+/osssuY2RkZLflLr30Ulav%0AXt3+BklasHYEE46Z6CEDAwP+4c4VmTK7u5/ZfBmOSjq/aIajFziLSFI1x0yoJ7XqzW52dpbx8fG6%0Ag1sr+9auXcvs7GzxRnYxZxFJqmYwoZ7Uqjc7FwWrrzKLqHbQb0VEsGrVqr6eRST1E4MJ9aRWvdmZ%0Azq/PWUSSqhlMqCe16s3OdP78RkdHmZycZOXKlTvsL5VKfTmOROpnzuZoIWdTdJ5mp8xWZoXsblGw%0Afp4C6e+91F2cGprrxGDCqYOdq9k3u8psDmCHgKLR9SokaSkZTOQ6LZho9eJI6jwuCiapVxhM5Dop%0AmHAlwP5hOl9SL3DRqg7UysWR1NlcFEyS6nM2R5OcOihJ6ncGE01y6qAkqd8ZTDTJlQAlSf2u5cFE%0ARJwSEalmu7nqeORlNkXEPRFxWUQc0up2LBZXAlQvmp2d5bLLLuOrX/0ql112Wd89e0RSMe3KTPxf%0AYLBqe2rVsfcB7wLeARwB3Ax8NyL2bVNb2s6VANVLyuUyQ0NDjIyMsGbNGkZGRhgaGqJcLi910yR1%0AqJZPDY2IU4CXpZQOq3MsgE3AupTSP+b7lgG3AO9PKZ2+wNfomKmhMDdlcHp6mltvvZX999+flStX%0AOnVQXcc1U6Te101TQx8fEZuA7cCVwF+llP4LeCxwEHBhpWBKaXtEfA84BqgbTOQBx7KqXR2TxdjV%0AypcGEuomu3vcekSwdu1aTjzxRH+3Je2gHd0cVwKvA/4b8GdkwcPlEfGI/N+QZSKq3VJ1rJ6Tga1V%0A2/wLOyyiyqe42nUmpqenGRsbMy2sruLj1iU1quXBRErp/JTS11NK16WULgJOyA+9vrpYTbWos6/a%0AR4EVVVupVe1t1O4+xQGsXbvWgWvqGq6ZIqlRbZ8amlK6C7gOeDzZYEvYOQtxADtnK6rPsT2ltK2y%0AAXe2pbEF+ClOvcY1UyQ1qu3BRD7e4cnADLCeLKA4rur4XsBzgMvb3ZZW8lOceo1rpkhqVDvWmTgt%0AIp4TEY+NiCOBSWA58KWU5f/XAX8VES+PiEOBLwJ3A2e1ui3t5Kc49RrXTJHUqHZkJkrAV4EbgTJw%0AH3BUSunX+fFTyQKKfwauAlYCx6eUlrzrogg/xakXuWaKpEb4CPImVGZzADsMxHROvrqdj1uXelc7%0A1pkwmGhSvXUmVq1axbp16wwkJEkdx2Ai10nBBPgpTpLUPbppBcy+MjAwwOrVq5e6GZIkLQkfQS5J%0AkppiMCFJkppiMCFJkppiMCFJkppiMCFJkprS1bM5tm1ryYwWSZL6RjveO7t1nYmVwPyP7JQkSbtT%0ASilNt+JE3RpMBPAoOuBR5MC+ZIFNic5oT7t5vb3N6+19/XbNXu/85TalFgUBXdnNkV98S6KpZlU9%0A6OvOVq0k1sm83t7m9fa+frtmr3deLf1ZOABTkiQ1xWBCkiQ1xWCieduBD+df+4HX29u83t7Xb9fs%0A9S6CrhyAKUmSOoeZCUmS1BSDCUmS1BSDCUmS1BSDCUmS1BSDiRoRsV9EnBkRW/PtzIh4+G7qLIuI%0AT0XEbRFxV0R8MyJKVcffEBFpnu2AvMzqeY4/qduuNy9T71reVlPmqRHxvYi4JyKmI+KDUbXiSju0%0A6f4+PSK+GhEb8mu5ISLGa86xKPc3Iv4iItZHxL0RcXVEDO+m/Csi4ucRsT3/+vKa4xERp0TEpvza%0ALouIQ2rKFP6ZtlIrrzki9oyIf4yI6/J7vSki/i0iHlVzjpvq3Mt/aNc11rx2q+/xF+tcyw9ryuz2%0A/3y7tOF65/tb/N6qMl1xfyPikIj4elV71zZyzpbc35SSW9UGnA9cBxydb9cB5+6mzmfJli99PvAM%0A4BLgp8BAfnxv4KCa7TvAZVXnWA0k4Ak15Qa67XrzMgl4Q8217F11fDlwM/BV4FBglGxFtnd32/UC%0AbwI+CTwHeBzwWuBu4B2LeX+BVwL3AW8BngysA34HPHqe8kcD9wMnA0/Kv/4eOLKqzPvz+zKa36f/%0ADWwC9m3mZ9qp1wysAL4L/CnwROAo4IfAVTXnuQn4QM29fFi3XW9e5ov5Pay+lj8s8n+gy6639m/x%0AG4EHgMd14f09AvgY8CpgBljbyDlbcX/b/p+9m7b8B51qfvGOyvc9cZ46K/Ib9cqqfY8CZoH/Nk+d%0A/fM6J1XtW52/zsN74Xrzc7xsF6/9duAOYFnVvv9Btkx6dNv11qn3GeCSxby/wJXAZ2v23QB8dJ7y%0AZwPn1+z7DvDV/N+R/4F6f9XxZfl9e2ujP9NOvuZ56hyRX0/1H9+bqPOHuxuvlyyY+MYuXrOh/wOd%0Aer116nwDuLhmX1fc34W0eXfnbNX9tZtjR0cDW1NKV1Z2pJR+CGwFjpmnzuHAnsCFVXU2Adfvos7r%0AyD65TtY5dk1EzETExRExUvwSCmn39X46T5v9OCLeFhHVv29HA99LKVUvrHIB2S/xUIPXszuLdX8h%0A+w+6pc7+ttzfiNgrb+uFNYcuZP52Hl2n/AVV5R9L9oms+tq3A9+rKtPIz7Ql2nTN9awgCybuqNn/%0A/oj4bUT8NCL+Z96etmnz9a6OiM0R8cuIOCPy7tdco/8HmrIY9zciDgROAL5Q53A33N9WnLMl97cr%0AH/TVRgcBm+vs35wfm6/OfSml22v237KLOm8Czkop3VO1bwb4c+Bqsk9/JwEXR8TqlNL3F9j+otp5%0AvR8ALgbuAZ4HfBx4JPC3Vee5qc45KsfW7775hS3K/Y2Io8nS5CdU7W73/X0kMMDcz3C37cz376r8%0AQVX7ass8pqpM0Z9pq7TjmncQEX8A/APZ/9fqByNNAD8BbgeeBXyULPh6S4H2F9Wu6z0f+Hfg12TX%0A8DfAJRFxeB48NvI3rhXafn+B15M9WbNcs79b7m8rztmS+9sXwUREnAJ8aDfFjsi/1lsSNObZv8uX%0ArVcnf6N5Cll24kEppRuBG6t2XRERq4D3AIXebDrhelNKf1t17KeRjav8IHPBRL3Xjnn27/qFO+B6%0Aq9pyCHAO8JGU0ncr+1t5f3ej3s90V9e2kPK7K9Oqn2mj2nHNRMSeZGNE9gD+YocTpPRPVd9eGxG3%0AA5MR8f6U0m8X2vAGtfR6U0pnVx27PiKuIgssTmDnN9kir9sqbbm/uTcBX0kp3bvDCbrr/rbrnIVe%0Aty+CCeDTZH8UduUm4GnAgXWO7c/OkV3FzcBeEbFfTWR3AHB5nfJvAX6aUrp6N+2BbODXaxdQrlYn%0AXW/FD4HlEXFgSumW/Dy1UW8ltTrfa8+nI643Ip5CNnDpjJpgaj6N3t96biPr46z3M93Vte2q/M35%0A14PIMivzlSn6M22Vdlwz8GAg8TWyT6PPTbt/dHVl9sPBQLvebNp2vdVSSjMR8Wvg8VXnaOT/fLPa%0Aer35jIYnkg1Q3J1Ovb+tOGdL7m9fjJlIKd2WUvrFbrZ7gSuAFRHxrErdiDiSrM90vh/q1WSjhY+r%0AqjNINvK99s3mYWTp73r9c/U8gx3/iC9Ip1xvnWu5l7l+5yuAY2v6IY8nmylwU7ddb56RuBT4Ukrp%0Afy6w6Q3d33pSSvflbT2u5tBxzH9tV9Qpf3xV+fVkf2iqr30vslkrlTKN/Exbok3XXB1IPB54/gI/%0AiT4j/9qS+1lPu663VkQ8AljF3LU0+n++KYtwvW8Grk4p/WwBzenU+9uKc7bm/jYy4rSXN7L+w5+R%0AjUg/CriWqmluwErgF8CzqvZ9FthANjbgGWRjBXaaVkP2y3sPsF+d110LvIzsD9ghZH10CRjttusF%0AXgL8Wf7L+Edk2ZitwETVOVaQvVGdlZd7eV5mMaaGtvp6DyEbI/BldpxKtv9i3l/mpoC9iWyWxT+R%0ATQF7TH7836gaFU42uOp+sumfT8q/1psaekd+fw7N71e9qaHz/kzbfD9bes1k2dpz8vv99Jr7uVde%0A5mjgncBhZJmLPyWbhXROF17vw4DT8msaIpt1dDnZNMHqe7ygv3Gdfr1V5ZYDdwFvq/Oa3XR/98rb%0AeRjZ/8uP5f8+eKHnbNX9bft/9m7bgD8ke1PYlm9fpmo6X/4fLgGrq/b9AfApsvTX3cC5wKo6576c%0ArH+u3uu+D/h/ZMHGFmAKeFE3Xi/wAuAasoFNd5GtOzAOPKTmtZ9KNl7gXrKI/0O0aVpom6/3lLxO%0A7XbTYt9fsr79m8geP3w1cGzVscuAL9aUHyMLnu4jmy42WnM88uubye/T94BDi/xMF+F3uGXXXHX/%0A622r8zJ/TJb2viO/n7/If0YP7cLr3ZtstsPm/PivyaaKrqo5x4L+xnX69VaV+fP8OlbUOdY193cX%0Av6+XLfScrbq/PoJckiQ1pS/GTEiSpPYxmJAkSU0xmJAkSU0xmJAkSU0xmJAkSU0xmJAkSU0xmJAk%0ASU0xmJAkSU0xmJAkSU0xmJAkSU0xmJAkSU0xmJAkSU35/1+4wxQJMXyYAAAAAElFTkSuQmCC" alt="" />




具体实现:
 (theta_0, theta_1同时更新)
(theta_0, theta_1同时更新)
可以我用jupyter写的版本(格式会好看点):https://douzujun.github.io/page/%E6%95%B0%E6%8D%AE%E6%8C%96%E6%8E%98%E7%AC%94%E8%AE%B0/5-%E5%9B%9E%E5%BD%92%E7%AE%97%E6%B3%95/Code/%E9%80%BB%E8%BE%91%E5%9B%9E%E5%BD%92%E4%B8%8E%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D_GradientDescent.html
实验数据下载:https://github.com/douzujun/douzujun.github.io/tree/master/page/%E6%95%B0%E6%8D%AE%E6%8C%96%E6%8E%98%E7%AC%94%E8%AE%B0/5-%E5%9B%9E%E5%BD%92%E7%AE%97%E6%B3%95/Code
# coding: utf-8
# In[3]:
get_ipython().run_line_magic('matplotlib', 'inline')
import pandas as pd
import matplotlib.pylab as plt
# Read data from csv
pga = pd.read_csv("pga.csv")
# Normalize the data 归一化值 (x - mean) / (std)
pga.distance = (pga.distance - pga.distance.mean()) / pga.distance.std()
pga.accuracy = (pga.accuracy - pga.accuracy.mean()) / pga.accuracy.std()
print(pga.head())
plt.scatter(pga.distance, pga.accuracy)
plt.xlabel('normalized distance')
plt.ylabel('normalized accuracy')
plt.show()
# ### accuracy = $\theta_1$ $distance_i$ + $\theta_0$ + $\alpha$
# - $\theta_0$是bias
# In[4]:
# accuracyi=θ1distancei+θ0+ϵ
from sklearn.linear_model import LinearRegression
import numpy as np
# We can add a dimension to an array by using np.newaxis
print("Shape of the series:", pga.distance.shape)
print("Shape with newaxis:", pga.distance[:, np.newaxis].shape)
# The X variable in LinearRegression.fit() must have 2 dimensions
lm = LinearRegression()
lm.fit(pga.distance[:, np.newaxis], pga.accuracy)
theta1 = lm.coef_[0]
print (theta1)
# ### accuracy = $\theta_1$ $distance_i$ + $\theta_0$ + $\alpha$
# - $\theta_0$是bias
# - #### 没有用梯度下降来求代价函数
# In[9]:
# The cost function of a single variable linear model
# 单变量 代价函数
def cost(theta0, theta1, x, y):
# Initialize cost
J = 0
# The number of observations
m = len(x)
# Loop through each observation
# 通过每次观察进行循环
for i in range(m):
# Compute the hypothesis
# 计算假设
h = theta1 * x[i] + theta0
# Add to cost
J += (h - y[i])**2
# Average and normalize cost
J /= (2*m)
return J
# The cost for theta0=0 and theta1=1
print(cost(0, 1, pga.distance, pga.accuracy))
theta0 = 100
theta1s = np.linspace(-3,2,100)
costs = []
for theta1 in theta1s:
costs.append(cost(theta0, theta1, pga.distance, pga.accuracy))
plt.plot(theta1s, costs)
plt.show()
# In[6]:
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
# Example of a Surface Plot using Matplotlib
# Create x an y variables
x = np.linspace(-10,10,100)
y = np.linspace(-10,10,100)
# We must create variables to represent each possible pair of points in x and y
# ie. (-10, 10), (-10, -9.8), ... (0, 0), ... ,(10, 9.8), (10,9.8)
# x and y need to be transformed to 100x100 matrices to represent these coordinates
# np.meshgrid will build a coordinate matrices of x and y
X, Y = np.meshgrid(x,y)
#print(X[:5,:5],"\n",Y[:5,:5])
# Compute a 3D parabola
Z = X**2 + Y**2
# Open a figure to place the plot on
fig = plt.figure()
# Initialize 3D plot
ax = fig.gca(projection='3d')
# Plot the surface
ax.plot_surface(X=X,Y=Y,Z=Z)
plt.show()
# Use these for your excerise
theta0s = np.linspace(-2,2,100)
theta1s = np.linspace(-2,2, 100)
COST = np.empty(shape=(100,100))
# Meshgrid for paramaters
T0S, T1S = np.meshgrid(theta0s, theta1s)
# for each parameter combination compute the cost
for i in range(100):
for j in range(100):
COST[i,j] = cost(T0S[0,i], T1S[j,0], pga.distance, pga.accuracy)
# make 3d plot
fig2 = plt.figure()
ax = fig2.gca(projection='3d')
ax.plot_surface(X=T0S,Y=T1S,Z=COST)
plt.show()
# ### 求导
# In[21]:
# 对 theta1 进行求导
def partial_cost_theta1(theta0, theta1, x, y):
# Hypothesis
h = theta0 + theta1*x
# Hypothesis minus observed times x
diff = (h - y) * x
# Average to compute partial derivative
partial = diff.sum() / (x.shape[0])
return partial
partial1 = partial_cost_theta1(0, 5, pga.distance, pga.accuracy)
print("partial1 =", partial1)
# 对theta0 进行求导
# Partial derivative of cost in terms of theta0
def partial_cost_theta0(theta0, theta1, x, y):
# Hypothesis
h = theta0 + theta1*x
# Difference between hypothesis and observation
diff = (h - y)
# Compute partial derivative
partial = diff.sum() / (x.shape[0])
return partial
partial0 = partial_cost_theta0(1, 1, pga.distance, pga.accuracy)
print("partial0 =", partial0)
# ### 梯度下降进行更新
# In[22]:
# x is our feature vector -- distance
# y is our target variable -- accuracy
# alpha is the learning rate
# theta0 is the intial theta0
# theta1 is the intial theta1
def gradient_descent(x, y, alpha=0.1, theta0=0, theta1=0):
max_epochs = 1000 # Maximum number of iterations 最大迭代次数
counter = 0 # Intialize a counter 当前第几次
c = cost(theta1, theta0, pga.distance, pga.accuracy) ## Initial cost 当前代价函数
costs = [c] # Lets store each update 每次损失值都记录下来
# Set a convergence threshold to find where the cost function in minimized
# When the difference between the previous cost and current cost
# is less than this value we will say the parameters converged
# 设置一个收敛的阈值 (两次迭代目标函数值相差没有相差多少,就可以停止了)
convergence_thres = 0.000001
cprev = c + 10
theta0s = [theta0]
theta1s = [theta1]
# When the costs converge or we hit a large number of iterations will we stop updating
# 两次间隔迭代目标函数值相差没有相差多少(说明可以停止了)
while (np.abs(cprev - c) > convergence_thres) and (counter < max_epochs):
cprev = c
# Alpha times the partial deriviative is our updated
# 先求导, 导数相当于步长
update0 = alpha * partial_cost_theta0(theta0, theta1, x, y)
update1 = alpha * partial_cost_theta1(theta0, theta1, x, y)
# Update theta0 and theta1 at the same time
# We want to compute the slopes at the same set of hypothesised parameters
# so we update after finding the partial derivatives
# -= 梯度下降,+=梯度上升
theta0 -= update0
theta1 -= update1
# Store thetas
theta0s.append(theta0)
theta1s.append(theta1)
# Compute the new cost
# 当前迭代之后,参数发生更新
c = cost(theta0, theta1, pga.distance, pga.accuracy)
# Store updates,可以进行保存当前代价值
costs.append(c)
counter += 1 # Count
# 将当前的theta0, theta1, costs值都返回去
return {'theta0': theta0, 'theta1': theta1, "costs": costs}
print("Theta0 =", gradient_descent(pga.distance, pga.accuracy)['theta0'])
print("Theta1 =", gradient_descent(pga.distance, pga.accuracy)['theta1'])
print("costs =", gradient_descent(pga.distance, pga.accuracy)['costs'])
descend = gradient_descent(pga.distance, pga.accuracy, alpha=.01)
plt.scatter(range(len(descend["costs"])), descend["costs"])
plt.show()
distance accuracy
0 0.314379 -0.707727
1 1.693777 -1.586669
2 -0.059695 -0.176699
3 -0.574047 0.372640
4 1.343083 -1.934584
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAhoAAAFwCAYAAAD+PtKHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz%0AAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBo%0AdHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzt3XucHFWZ//HPMyEXEjITQsQZUCQb%0AQBgCBhAWBFFiskYxoLguhGVXxOVqdgFdRbwFZFeNuyug3BRZvLCAuiohC0aJ4WIwyCUGGIefhJCE%0A2wyYDMyE3Mmc3x/VnXR6urqrqqu6qru/79drXpnp6e46Xd2T89Q5z3mOOecQERERSUJL2g0QERGR%0AxqVAQ0RERBKjQENEREQSo0BDREREEqNAQ0RERBKjQENEREQSo0BDREREEqNAQ0RERBKjQENEREQS%0Ao0BDREREEqNAQ0RERBKzS9oNqCUzM2AvYF3abREREalDY4GXXIiN0poq0MALMl5IuxEiIiJ17C3A%0Ai0Hv3GyBxjqA559/ntbW1rTbIiIiUjcGBgZ461vfCiFnBZot0ACgtbVVgYaIiEgNKBlUREREEqNA%0AQ0RERBKjQENEREQSo0BDREREEqNAQ0RERBKjQENEREQS05TLWyWbtg06Hl7ZxyvrNrHn2FEcNXE8%0Aw1os7WaJiEgVFGhIJizo6uHy+d309G/afltH2yjmzOxkxuSOFFsmIiLV0NSJpG5BVw/n37J0pyAD%0AoLd/E+ffspQFXT0ptUxERKqlQENStW3Qcfn8bkrtzpO/7fL53WwbDLx/j4iIZIgCDUnVwyv7hoxk%0AFHJAT/8mHl7ZV7tGiYhIbBRoSKpeWecfZES5n4iIZIsCDUnVnmNHxXo/ERHJlroJNMzsfDN7wswG%0Acl9LzOwDabdLqnPUxPF0tI3CbxGr4a0+OWri+Fo2S0REYlI3gQbwAvB54J25r0XAPDM7ONVWSVWG%0AtRhzZnYCDAk28j/PmdmpehoiInWqbgIN59x859zdzrmnc19fBF4Hjk67bVKdGZM7uP6Mw2lv23l6%0ApL1tFNefcbjqaIiI1LG6LNhlZsOAjwFjgCVl7jcSGFlw09iEmyYRzZjcwfTOdlUGFRFpMHUVaJjZ%0AIXiBxSi80YyPOOe6yzzkUmBOLdom1RvWYhwzaY+0myEiIjGqm6mTnD8DU/CmS64HfmhmnWXu/3Wg%0AreDrLYm3UERERLarqxEN59wW4Jncj4+a2ZHAhcC5PvffDGzO/2ymYXgREZFaqrcRjWLGzjkYIiIi%0AkiF1M6JhZl8DfgU8j5fUeRrwXmBGis0SERGRMuom0ADeDPwY6AD6gSeAGc65e1JtlYiIiPiqm0DD%0AOffJtNsgIiIi4dR7joaIiIhkmAINERERSYwCDREREUmMAg0RERFJjAINERERSYwCDREREUmMAg0R%0AERFJjAINERERSYwCDREREUmMAg0RERFJjAINERERSYwCDREREUmMAg0RERFJjAINERERSYwCDRER%0AEUmMAg0RERFJjAINERERSYwCDREREUmMAg0RERFJjAINERERSYwCDREREUmMAg0RERFJjAINERER%0ASYwCDREREUmMAg0RERFJjAINERERSYwCDREREUmMAg0RERFJjAINERERSYwCDREREUnMLmk3QCRp%0A2wYdD6/s45V1m9hz7CiOmjieYS2WdrNERJqCAg1paAu6erh8fjc9/Zu239bRNoo5MzuZMbkjxZaJ%0AiDQHTZ1Iw1rQ1cP5tyzdKcgA6O3fxPm3LGVBV09KLRMRaR4KNKQhbRt0XD6/G1fid/nbLp/fzbbB%0AUvcQEZG4KNCQhvTwyr4hIxmFHNDTv4mHV/bVrlEiIk1IgYY0pFfW+QcZUe4nIiLR1E2gYWaXmtkj%0AZrbOzF4xszvM7O1pt0uyac+xo2K9n4iIRFM3gQbwHuBa4GhgOt6Kmd+Y2ZhUWyWZdNTE8XS0jcJv%0AEavhrT45auL4WjZLRKTp1E2g4Zyb4Zz7gXPuT865x4FPAPsAR6TcNMmgYS3GnJmdAEOCjfzPc2Z2%0AZqKexrZBx5IVa5m37EWWrFirBFURaSj1XEejLfevbzafmY0ERhbcNDbRFkmmzJjcwfVnHD6kjkZ7%0ABupo5IuI3dPdyx3LXqJv/Zbtv1OdDxFpJOZc/V09mZkB84DdnXPvLnO/y4A5xbf39/fT2tqaXAMl%0AU/Kdem//RvrWb2H8biNpb02vQmipImKF8i26/ozDFWyISGYMDAzQ1tYG0OacGwj6uHod0bgGOBQ4%0ArsL9vg58q+DnscALSTVKsmlYi9G/cQvf/PWfa1Yh1K/seb6IWLnw3uEFG5fP72Z6Z3smpndERKKq%0Au0DDzL4DnAQc75wrGzQ45zYDmwsem3DrJIv8Ovd8hdC4Rw78yp5/+cROrrirdBGxYoV1Po6ZtEds%0AbRMRqbW6CTRy0yXfAT4CvNc5tzLlJkkdqFQhNO6Rg3JBzQW3Lg39fH51PrRRnIjUi7oJNPCWtp4O%0AnAysM7P23O39zrmN6TVLsixMhdBqRw6ClD0Pq1SdD20UJyL1pG6WtwLn4600uQ/oKfg6NcU2ScbV%0AskJopaAmDL86H9ooTkTqTd2MaDjnNC4sodWyQmhc5cz96nzUehooKk3riEihugk0RKLIVwjt7d9U%0AsoM2vLoacVQIDROsGP7TKX51Pmo5DRSVpnVEpFg9TZ2IhFbLCqFBy55fd/phtLftHJSMHzOcTx67%0AL7edfTSLL5laslPO+kZxmtYRkVI0oiENr1YVQvNBzfm3LB0yYlEY1MyY3MH7J3eEnl7I8kZx9TKt%0AIyK1p0BDmsKMyR1M72xPPHcgaFAzrMVCT29UmgaC9DaKq4dpHRFJhwINaRpROvdy/JIekwpqyo2Y%0A5G3cuo17untrng+R9WkdEUmPAg2RCColPcYd1OTlR0w+/4sneW3D1iG/79+wNZFqp5VkeVpHRNIV%0AOhnUzN6bQDtEEhP3NuxpJz1O72xn1C6l/3Tzr+zy+d2BX2cc5+eoieMZN3q47+/96oKISOOLMqKx%0AwMxeBG4Gfuicez7mNonEptrllsXTI0e8bffUkx4fXtlH78Bm39+HyYeIaznqPd29JUdYCtsU1+oe%0AEakvUQKNvYAzgDOBy8zst8BNwB3OuS0xtk0aXNKFnardTK1UJzx+zAj61vt/zGuR9BhXPkRcm83l%0AV5yUM270cKZ3tpe9j4g0ptCBhnOuD/g28G0zmwKchbcPyfVm9j/ATc65x+NtpjSapAs7Vbvc0q8T%0ALhdkFEoy6TGOfIg4l6MGKb3+2oatWnEi0qSqKtjlnFsGfAMv0BiDF3Q8Zma/M7ODY2ifNKBa5DiE%0AWW5ZrFwnHFSSSY9BC4MdNXG8b/5FNeenmFaciEg5kVadmNlwvF1UzwKmA48Cs4HbgPHAXOBnQGc8%0AzZR6VGpqBKhJjkM1nV81m6PFWdLcT9DCYPd09/qOGm1+YzDQsYKcR604EZFyQgcaZvYdYFbux1uA%0Azznnugrust7MPg+sqr55Uq/8pkZOO/KtNSnsVE3nF/XKO+6S5uVUKgwGlM2/uGjaAYGOE+Q81nI/%0AGRGpP1FGNDqBfwZ+Xib58yXghMitkrpWLsnwyoXLAz1HtcPs1XR+QYOU8WOG07d+x0qLuEuaV+JX%0AGAzguLmLyo4a3f7Ic7S3juTlgc1VBwdBR1i04kSkOUVJBn1fgPu8AdwfqUVS1yolGQZV7TB7NZ1f%0A0CDl/s+ewGOrX011O/RShcGWrFgbaNTo4mn7c9XC5bEEB7XaT0ZE6k+UqZNLgZedc/9ddPtZwJuc%0Ac3PjapzUn2ryGyDeYfaonV/QIGXELi2ZXEURdDRo3wljYg0OarWfjIjUlyhTJ+cCp5e4/U/A7XiJ%0AoNKkwkx51GKYPWrnV89X6GHyU46ZtEeswUFSpddFpH5FCTTagVLrD/8CZPd/X6mJoJ3cxdMO4PZH%0AnqtJJ17c+eWXfFbqWOv1Cj1sfoqCAxFJUpRA43ngWGBl0e3H4iWBShML2snNnrofs6fuF7oTr7aa%0AaNhCYfXYCSs5U0SyxJwLV5bIzC4BPpv7WpS7+X3AN4H/cs59PdYWxsjMWoH+/v5+Wltb025Ow8qv%0AOoHSnVzUnUWrrSbqtxqm2nZlVTXnK+ny8CJSfwYGBmhrawNoc84NBH1clEDD8KqB/gswInfzJmCu%0Ac+6roZ6sxhRo1E7cJcarDRK2DTqOm7vIN1E1P9Ky+JKpDdWhRgkYki4PLyL1qWaBxvYHmu0GHARs%0ABJY75/y3k8wIBRq1FddVcdggodRxH17Zx6wbH6p4rNvOPrrupkri1GyjPiISXNRAI1IJcgDn3OvA%0AI1EfL40vrvyGMPty9G/cUvJq/AOTg+0cWo/7ccQZ0NWiPLyINJeoe50cCXwM2Icd0ycAOOdOiaFd%0AItsF7fzv6e7l5gdXlaxI+t8Prgr0HPW2H0ec0xxhArpmHvURkXBC795qZqcBD+KVIv8IMDz3/VSg%0AP9bWiRC8879j2Utlr8bLXYQX7nhaL+LeBVe7sIpIEqJsE/8F4GLn3IeALcCFeLkaPwWei7FtIkCw%0AbdG9fUf8tt7xgo3cDulDnqcel3wGKfV++fzu7dvCB6FdWEUkCVECjUnAXbnvNwNjnJdReiVwTlwN%0AE8nL14UA/yDhI1P2DvRcnzx2X9rbdu4o29tG1V2SY5hpjqCCBHSVRn3yxdDmLXuRJSvWhgp0RKQx%0ARcnR6APG5r5/EZgMPAmMA0bH1C6RnVQqCd626whuCpCHMa2znS+c2Fn3NSKSmOaottCXlsWKSClR%0AAo3fAdPxgoufAleb2dTcbb+NsW0iOylXEnzboAtcdrseq30WS2qaY3pnOxdNO4CbH1zJaxu3br+9%0AUnl4v2Wx+XyRehsxEpH4RAk0ZgP5/72+DmwFjgN+AVwRU7tESvILEpqt7HbY/UyCKDUiMW7X4Xzi%0A2H2ZPXV/33OnZbEiUk6oHA0z2wWYCQwCOOcGnXPfdM6d5Jz7tHPu1SQaKRJEfnqlEXIwKgmStxIm%0AsPJbwdK/cStXLVzOPd29vo8Nmi/y0LNrA7VFRBpLlBLkG4CDnHOrk2lSclQZtL5ELUSVxX06wrQp%0AzH3jyIuotjz7vGUvcuHtyyoeZ9yuw/nGRw9pqIBPpJnUsjLoH4DDgLoLNKR+VNOBZi0HI8xrCfu6%0A49jKvtpCXUHzQF7buFX5GiJNKMry1uuA/zKz2WZ2jJkdWvgVdwOzTEv5khF3Iao0hXktUV93PrA6%0AecreHDNpj5JBRrnParUrWCotiy0Wtr5HJfo7FMm2KCMaP8n9++2C2/I5Xw4YVm2j6oGW8iUjicTC%0AtKZSwrwWct8nkVBZ6bNa7QqWwkTcSuIuY66/Q5HsizKiMbHE118V/NvwGumKO2viLkS1oKuH4+Yu%0AYtaND3Hh7cuYdeNDHDd3UU3eozCvJYkCXBDssxpHoa58Iu64XYcHalccZcz1dyhSH0IHGs651eW+%0AkmhkliRR+ll2iKMQVX4o/Yr5f+K8FDuiMK8liQJcQT+rQCwrWGZM7uDa0w8P1LZqy5jr71CkfoSe%0AOjGzfyz3e+fcj6I3p+Kxjwc+CxwBdAAfcc7dkdTxStEOl8kKM4xfakrknu7eIUPpxWpV2yGJolph%0A7hvms1qp8mrQaYijJ+0Re32PUvR3KFI/ouRoXF3083C80uNbgA1AYoEGMAZ4HLgZ+HmCx/GlHS6T%0AFbQQ1avrtwxZkjlu9HBe27C1xKOGqkVHFLaoVtwddNjPahwrWGpVOE1/hyL1I8rUye5FX7sBbwcW%0AA7Nib+HOx/6Vc+5LzrlfJHmccrTDZbKCFKI66R0dfOrWoVMiQYOMQkl2RGGKasVdgAuifVaDrGCp%0ApBaF0/R3KFI/oiSDDuGcWw58nqGjHakys5Fm1pr/YsdmcJHFkTgn5ZXrqK49/TDufLyn5FV/FEl3%0ARGE63bg76DQ/qzMmd7D4kqncdvbRXH3aFG47+2gWXzI1tpUg+jsUqR+hK4P6PpHZYcD9zrmalNw0%0AM0eFHA0zuwyYU3x7tZVB89nuUHpoWAWJ4lEqB+PhlX3MuvGhqp+7UrXLuCVVGbSSev6sVjoP9fza%0AROpR1MqgUUqQn1R8E15i5mzgeefcB0I9YUQBA42RwMiCm8YCL8RRglzr99MRtNx1OY3QEdWiTHma%0ApdyDtll/hyK1U8tAY7DoJgf8BVgEfMY5V5PF60ECjRKPiXWvkyzuqdHolqxYW/WIRr13RFE617Cf%0A1TQ7cL8t5/0CRP0ditRGzQKNrMhCoCG1l98AzG91Rin51Q9nHbsv0zvb67ojCtsJZ/UYfqrd4E1E%0AkhM10IglGbRWzGw3M5tiZlNyN03M/bxPqg2TmgmyOmPc6J2rU7a3jeKGMw7nKzMPjrySIk35AmS/%0A/OOLfOGXTyZapCrtQlhJVUgVkfREKdj1v8CjzrlvFN3+WeAo59zH4mpcCe8E7i34+Vu5f38InJng%0AcSVDKhWXqrYWRJaUmsLwE0dtkFoWwio15aH6GMnSNJOkIUrBrvcAl5e4fQHwr9U1pzzn3H0MvZCV%0AJlSpuFQjVIP0m8KoZGF3b+TXX6uO3i8H5NR3viXQ4yfsNrLynWQnSpyVtEQJNHbDqwJabCugxAep%0AmXxxqUZUbgqjkpseXMWRE8dH6jxqUQjLL4Dq7d/EVb99JtiT1GdqWWrKnfPzb1la1yuwJPui5Gh0%0AAaeWuP00oLu65og0rnyuxbxlL7JkxdqyeQ6VpjAqiZpHUakQFng5MIODLtLzb3ljsGKeSRBr1m8O%0AfexmlXbejUiUEY0rgJ+b2SS8Ja0A78MrP55kfoZI3Qo7bF3t1ETUPIrCvUr8vLZhK39/0x9CD7sv%0A6OrhC7/som99+FLxxVRaPDhtQCdpi7LXyZ3Ah4H9gOuA/wLeAkyr9U6qIvUgP2wdZrv6ODrSaoKV%0AtqKVO6WUa3+x/DnoW19q1jU4lRYPTwm2krZIy1udc3c55451zo1xzk1wzk11zt0fd+NE6l3UYesg%0AUxiVRAlW8gFBkA3qgg67R803iWtzuWanDegkbaEDDTM70sz+usTtf21m74ynWSKeMHkNWRS1LkS5%0AeiGVhL3qD1Knw0++/Vfe82ff9ydMvkm+7dednuzur7WW5udYG9BJ2qLkaFwLfBP4Q9HtewOXAEOC%0AEJEoGmE5XtDh6F/lph8Kl+j61QspJ+xVf5g6HeVcc+8Krrl3Rcn3J+yQfP7x75/cGPVQ0v4cF+bd%0A5Kvk5mmUSGohyl4nrwOHOueeLbp9IvCEc67qrdiTohLk9SPNMthxCrs3S6kOKF9kaWF3L79c9uJO%0AyZQtBoUXx2E6sKh1Osop9f6EOQfnHj+RSz/YGWOL0pWlz3HaAY/Uv1puqrYW+JBzbknR7e8C7nLO%0A7R7qCWtIgUZ9aKT9Liq9lmKVOqDiyo5HvG13Hlv96pCr/koVIMO2K4zi9yfoserpfQ0ii59jVQaV%0AakQNNKJMndwDfN3MTnbO9QOY2Tjga7nfiVSlkZbjDWsxTnpHB999YGWg+zu8Dujy+d1M72wf0gmU%0AKlJW/HOQK9dq63RUeg2F709+6P68MktmSz2u3mXxc9zIRe4ku6KsOvkM8FZgtZnda2b3AiuB9tzv%0ARKrSSMvxFnT18L2AQUZeNRuHBV1KW4tzV3iMGZM7eN+Bbwr9uHrWSJ9jkWqEHtFwzr1oZocCfw+8%0AA9gI3Azc5pyrvhKPNL0sLseLMuRcTRlxCN8BVVpKWzhSEnavkI62UXzxAwfy8rrN/GFlH7/pfrni%0AYwrfnwVdPfz2//0l0LEaZZllFj/HImmIMnWCc2498L2Y2yIC7FiO19u/qWSnmZ/brtVyvKhJdNVO%0AT4TtgEItpQ0R/Xz5xIPYs3UUX7nzT4EKbhW/P/kAKOzjKsl6vkHWPsciaYkUaACYWSewDzCi8PZc%0A5VCRyLK0HK+azaiiDokH6YBqucX671esCTwaUer9CRpwOapblhsk+KtlcJKlz7FImkIHGmb2V8Av%0AgUPYMSILO/6OhsXTNGlmfjUk2mu4HC/MVESpziLKkHiQDsivkz3tyH0CHSNsu4IGGVD6/Qka2Jx1%0A7L5VLcutFPylsbwzC59jkbRFGdG4Gi/5cxrwLHAUsAfenif/Gl/TpNnNmNzB9M70ijZVu2qg0tA5%0ADK2DUakDKrvF+sKnGTd6OP0btgYaqm9vHUXvQDyJiLNPmMSx+72p5PsTNLDZe9yubBt0Zd/fqMFf%0AmOAk7lGPtD/HImmLEmgcA0x1zv3FzAaBQefcYjO7FPg2cFisLZSmluZyvGqnIoIMnV8z6zB2HzMy%0AUAcUpJN9Y5vzDTJg55GSWUftw5ULn674+oLY/81jfd+nIAEXwBV3PcX3F68sG2hFCf6C7jczvbOd%0Ae7p7Exn10LJSaWZRlrcOA17Pfb8G2Cv3/Wrg7XE0SiRuUfaaiGPVQH7o3G/fjg8euhfHTNqDk6fs%0Avb3mhJ8gnezrm98o+btS+4TsO2G073OFVe4chNm3pdKOsFGCvyA5Ij39m7hm0TOhd9kVkcqijGh0%0AAYfiTZv8AficmW0BzsndJpIpUefm41o1ENfQedTk0g9MfjOnH/k2WoYZ85a9uP34YZe4+tljzIhA%0A5yDIvi2Vcl+CtrnwfkHP23X3PVN21OOyO//km4/TiLK+qkfqR5RA49+AMbnvvwT8H/A7YC1wakzt%0AEolFNatG4lw1EMfQedR6C7/qeplfde1c96KjbRR/9863VtWevCtOnhzoHOQDrh88uJIr7nrK935l%0Ac1+CLsstuN+qNesDPWTzG4Nlf987sJlrFj3DhdP2D9iIdFUTKGhfFIlTlIJdvy74/lmg08zGA6+6%0AsBuniCSo2lUjkK1VA0FzHYLo7d/E1b9dXnWbpnfuyQcPDX4OhrUYL722MdB9S41ErFm/OdBj8/db%0A0NXDlQurf515Vy58mre375b5zraaQKGa4FyklMh1NAo558LXShZJWFx7TWRh1UD+6vSDk9u56cFV%0AVT9fXFcEXS8OVFwpUmhBV0/g9pcawQmTNxO0UFhYlYLTtFUTKMQRnIsUiyXQEMmiOAtYpblqoNTV%0AafGy2LSE2RQsjgqhYfJmkto4Lo6N0JLKf6g2UMjiRnBS/xRoSMNqhL0m/K5O85OUnzh2X+Yte5G+%0A9eltMxQ0oIujQmiYvJmwybPFz1dONRuhJZn/UG2goI3gJAlRlreK1IX81a/fdaLh/QefxF4TUZbT%0AlnqOSlenC7p6+beTJ2NUXjqalKCBWlwVQistGc4/NmwAec7xE7k4YKJn1OA06O66UVUbKDRCcC7Z%0AoxENaVhp7TUR1xVr0KvTtl1HcNG0/bn5wVW8trF2IxthNwUL2jlN72yveJ8geTNhk2cP22d3pne2%0Ac9vDz/tWTK1mI7Ra5D9UGyhoIzhJQqARDTM7KehX0g0WCSPo1W9c4rxiDXp1+qlbl3LlwuXbg4wx%0AIypvNxS2Gyu+f5RALe4RpnzejF+xs3ygGSTIyHfyAJed1FlyhKja4DTU7roRVXuOyxVX00ZwElXQ%0AEY07in4u3Ewt/3OeNlWTTKnVqpG4r1iDXp0Wj2Js2LINgHGjh/PahtIjHO25TdiClCC/eNoB3P7I%0Ac1Uv701rhKncecgr7OSTWtJci/yHOM5xlpZ0S2MIFGg457aPfJjZNGAu8AVgCd5n+V14hby+kEAb%0ARapWi1UjcWfsR62bkb/vrsOHce0nD2fN+s1MGDMSDNa8vnl7oAVw+yPPVRwmnz11P2ZP3S+WQK2W%0AnZhfIm05+U4+ieC0VvkPcZzjLCzplsYRJUfjKuA859zigtt+bWYbgO8BB8XSMpE6E/cVa7mr0yB6%0A+jfx6Oo+Lpx2gO99wlz9xhWo1aITKze6VE5hJx93cFrL/Ic4zrE2gpO4RFl1MgnoL3F7P7BvVa0R%0AqWNxXrHmV61sfmOQi6btz5tbd97jY9yuwwMd68qFy8vmhdQ6hyWvUn5FtcLW0EhyBVJerfMfkj7H%0AIkFFGdF4BLjKzM5wzvUAmFk78F/Aw3E2TqSexHXFWmrVSnvrKC6edgD7ThjNnmNHMegcf//9PwRq%0AV5Ay6402TB4mz6GWSY7Kf5BmFCXQOAv4JbDazJ7L3bYP8DTw4bgaJlJvoibiFVaJXLVmA1ctfHpI%0AoPLywCauWvg0159xOMdM2oNtg46OtlGBrtqD5IU02jB5mDyHMJ18HBU9GzGwEyknyqZqz5jZocB0%0A4EC8/0O7gYXaVE2aXdgr1lKjF6WUWrUyZ2Yn592yNFC7mq2SY5BE2nGjh3PtrMM5OuC0QpwVPRst%0AsBMpx6qJDcxsFLC5XgIMM2sF+vv7+2ltbU27OdLAglz5RlkVAXDb2Udv76SuXrg80BLVwsc0i/z5%0AhdKjS2FyUPzeqyjPJVKvBgYGaGtrA2hzzg0EfVzoZFAzazGzL5vZi8DrwMTc7VeY2SfDPp9II6qU%0AiBd1VQTsPDoxe+p+tBclihaqRZJjOX6l2Le8MchNv3uWr8zr4qbfPcuWNwZjP3Zcia6V6qOAN9IU%0Apcx8FsVRPl+kUJQcjS8BHwc+B9xYcPuTwMXATTG0S6ShVbOzaPESzMtOOrjslXtalRz9phom793K%0Ab596ZafdZ//97qc4+90TufSDnbG2IY58iKD1Ua68588cu9+b6jrfIskN36R5RVne+o/AOc65/wG2%0AFdz+BF7ORqLM7AIzW2lmm8zsMTN7d9LHFIlblJwJv9GJOK7c476K9SvF3tO/iXu6Xxmyxf2gg+8+%0AsJKv3115G/mwql3mGfS9uubeFcy68SGOm7uo6s3R0pD0hm/SvKKMaOwNPFPi9hYg2OL+iMzsVLyC%0AYRcADwLnAr8ys07n3HNlHywSkzhWHoSt/lhpdKKaK/e4r2KrmRa68Xcr+czfHMiIXbKzsXTY9yrf%0AMddT3kYtNnyT5hUl0PgT8G5gddHtHwP+WHWLyvs0cJNz7vu5ny8ys/cD5wOXFt/ZzEYChRPYYxNu%0AnzS4uDrlsOXFgyzBjLKS4e4nXuKCW4f+2VbTWVYzLTTo4MdLVvHJd/9VpMcnIex7VY8dc9zl80UK%0ARblsuBy4xswuyT3+FDO7EW+fk6/G2bhCZjYCOAL4TdGvfoO310opl+JVLM1/vZBU+6TxxTm0HKRK%0A5MXT9ufq06Zw29lHs/iSqbGuEFRwAAAgAElEQVRfHd/9RA+zbyt9bVBNkmO1S2lX922o6vFxK/de%0A+SnsmOshubIWG75J84pSR2N+bgrjC3h/T18FlgIznXP3xNy+QhPwdoZ9uej2l4F2n8d8HfhWwc9j%0AUbAhESQxtJxmlcgFXT1ccGv5GhxRr2Kr3RTsbeNHV/X4IMJOf/m9V5Us7O7l0z9dlvnkylpt+CbN%0AKcrUCc65XwO/jrktgQ9f9LPvflPOuc3A5u13tOwPYUo2JTW0nEaVyG2Djs//4snA9690FVvcaR/x%0Att0j7ToL0GLwD8fsG/JR4USd/ip8rxYv/wvX3rei4rFuenDVkNuymMNRyw3fpPmEDjTM7L+B+51z%0APyy6vRW4yjl3VlyNK7IGb5VL8ejFngwd5RCJVZJDy7WuEnnNomd4bcPWwPdf/vLrLFmx1rfoWKlO%0A+6R3dPC9B1aG3nX27HdPTCQRNB8MLezurarzz79Xg84FCjRKyWIOR9Ty+SJBRPmLPhO4zsy+bWaF%0Aj98Vr75GIpxzW4DH8EqfF5oO/D6p44pA4wwtbxt03PzgylCPuebeZ4Ys29w26Lh64XLO88lZ+d4D%0AKznn+IlDltzuMWYE0w7ak+L+yoCZh7bzuRkHhX5NlSzo6uG4uYuYdeNDJYMMCJ+Tsub1zRXvU07h%0ACFiSwuSHpLWTrzS+SFMnwIl4xboOMrO/c869GmObyvkW8GMzexRYApyDt6HbDTU6vjSpNIeW41hO%0Am/fwyj5e2xh8NKNQT+6q/5zjJzJv2Uv0DpTubPNX7Hc+3sMXP3AgX5n/J/rWe8dcu34Lf3ppgG+f%0AOoX7nv4Ld3f1smHLNhww/4leHl29KNb8hTBl3sNMf8UVUBaPgMX5XkeZItKGb5KE0HudmNkg3vTF%0ANuDnwFuAmUAf8JJzbljcjSw6/gV4VUk7gC7gYufcAwEfq71OJLI4984Ic8w4a1zMW/YiF96+LM4m%0AhlZuOiXOc7lt0HHc3EWhl9pefdoUPnToXmU72/xzR8lDKVS4B02c77X2ZpEkRN3rJEqgsQ3ocM69%0AYma74I0mfAz4V+CGpAONaijQqC9xXt3FpZYlmpPoLJasWMusGx+KpX1JyY8OLb5kalXvd9TXOvPQ%0Adh5d/VrF97hS4Nk2ejj9G7aWHQH7z799B2vWb2bVmg1ctfDpWN7rSgFWXOdXmk8tA41BoN0590rB%0AbZ8G5gItCjQkDlnec6EWAVBSnUVcV+K1UO2Os3GO3vh1+OU+p4BvIOLwtqkPkpQb9r0OGmA1446+%0AUp2ogUaUHI0T8KZJtnPOfcvMngCOjfB8Ijvxu5LPyrLAWqwSSWo5bbnVBVlTbXGohd29MbXEf6VI%0ApZyGUrU3xo0ezqsbtgZe+RP2vVbxLcmaKAW77ve5fSGwsOoWSVNLe8+FrEzXJNlZ+BWf6mgbxZdP%0A7OQLv3wycsJonMolXFZ6n+5+oof5T8QXaIB/h18u8CwORCbsNpLP/DTaKEvQ97pRVkhJ4wgUaJjZ%0At4AvO+fW57735Zz7dCwtk6aU5p4LWZquSbqzKHclvvyV17ly4dORnhd2BCxX3NUdaYqm0gqeSu/T%0AtkHHl+Z1RW5/JWGDu8JAZMmKtb6rdSoJ+l6r+JZkTdARjcPYsTPrYWXul+WRWKkDaQ37Zm26phad%0Ahd+V+Oyp+3Hz71eGKuqV97eHv4WvnXIII3ZpoaVlR45CUJWKQwV5n9p2HUHf+i2h2x5U2OCucPRl%0A+cvrQh8vyHtdPMLz5RM7+dStKr4l2RAo0HDOnVDqe5G4pTHsm/Z0TSlpVmoc1mJ845RDOK9EkFAp%0AkfF/l77AgyvWbB9duP6Mw/nCL5/cXkejknL7vAR9nz4348BAxworSnBXavQl7DGh/HvtN8JzzvET%0AufPxnprvoyNSLGrBLpFE1GrYt/AKcM26zZncIjvNTddmTO7ghjLHnt7ZzjWLlnPlwuVDHls8CrRx%0A6yAX/6RyXsLsEyZx8fS3+3aoQafV+qqs2llKlOAuTLEwP5Xe63IjPN97YCXXnn4Yu48ZWdOco6zk%0AOUl2BM3R+EXQJ3TOnRK9OdLsanElH/UqM40s/TQrNZY79rZBx+2PPF/yccWjQO2twUafdh89ouzv%0Ag57/8WNG0NE2KvIoAkDbrrvQv/GN7T+37roLZx07kemdfhtF76zc6Iuf/Of94mn7s++EMRXf6yAj%0APFfc9VRN62VkKc9JsiPoXif9Ib5EqpLkngv5K8AonVBaWfr5XIqTp+zNMZP2GFKhMuheFmHuW+nY%0AYZJ286NUlbq6K+56aqf9VIoFPf/tbbsyZ2Zn2eOde/xEbjjj8CFBUEfbKM49fiK7Dt/5Gqx/4xtc%0AuXB52fYVqnR+Srd7FDeccTgXTjug5Hsd9hi12k8lz+9vKz/CFeS8SWMKmqPxiaQbIlIoiSv5KFeZ%0AkN0s/TBXj3FfaYZJ2g1Tu6Nc8m2YabVhLVZy2mmPMSO44uTJfPBQ77mLP2Ovrt/Cp271n+7oCZgc%0AHPT8zD5hP/Z/826RPt9ZqpeRxTwnyQ7laEhmxV0YK8pVZlaz9MOskkliRU3YpN38KNXnf/Fk2dUs%0AhbuoFndKYafVggSrhZ+xfNXUIIFopU4z6Pk5dr8JkT/jWaqXkeaydMm+KNvEY2Z/a2Y/NbOHzGxp%0A4VfcDRSJS5QruyxukV3p6hF2bHce5r5hVJoOMbwRk+JRoP6AS2b9hvzDTquVm3YqFjQQDTIlEfX8%0AhFGLYwSVpdEVyZ7QIxpm9i/AvwM/BE4GbgYmAUcC18baOpEYBb2y+/KJBzFh7MhMZMyXyuAPOzdf%0A61LmpUYXokxb9Q6UbndSCbJhO8Fy969FUnOaS6CLZWl0RbInytTJBcA5zrnbzOzjwDedc8+a2VeB%0AbE1iixQIOsd/5rETMzFN4pdX8cHJwVY+hOk44yxlXmpJZpRpq3LLVMNMqwVdbhm2E6x0/ziXJ/u9%0AhjSXQBdSNVIpJ0qgsQ/w+9z3G4Gxue9/DDwEzI6hXSKxy9IVYCXl8ipuenBVoOcI03EmUcq8UJRA%0AZvyY8stdgwiTBJvvLCsFRGE6zThGXyq9hjSXQOfV09+W1F6UHI1eIH8psRo4Ovf9RKi4gk0kVUku%0AnY1LkLyKFvP/Yyucm6/FPH6QPIgogUx7266R2wThl1vmO8sg/4mF6TTD5IkUC/oaqjlGXOrhb0vS%0AEWVEYxEwE1gK3ARcaWZ/C7wTCFzYSyQtWbgCLCfINEM+dzPI1WPSV5pBpiYqDa0Xqzb4ibrc0m8q%0AorBdtZqSSHLJaFLVO7P+tyXpiBJonENuJMQ5d4OZ9QHHAfOBG2Jsm0hi4l46G6eg0wxnHbsvv+rq%0A9Z2bz3cmm98Y5KJpB3Dbw8/tlGAZxzx+0KmJMLU0jOqDn2qWWxZ2lr39G+lbv4Xxu42kvbW2Jbwf%0AfOYviSTyJl29M8t/W5KO0IGGc24QGCz4+afAT+NslEgzCzrNML2znS+e2Fny6rFUZ9LeOnJ7eesJ%0Au40EB2vWb2bJirWROtAg9TmKr26vPf0wrrjrKd8ONK4Or9rllml1llHK44fJf8naLsXSHCIV7DKz%0AUcChwJ4U5Xk45+6MoV0iTStsBcziDtGvM3l5YDNXLVxeclfPsB18kDySz//iSS67s3unUZSONm8L%0A893HjOCVdZt2CnjiHGavx+WWUTdhC/oaVL1T0hKljsYM4EfAhBK/dsCwahslUu+qmQOvJoM/SADw%0A3QdWDvld2CvaIHkkXgXQnQt09fZv4lO3esc5ecreFY8TVb0tt4y6CVuY16DqnZKWKKtOrgF+BnQ4%0A51qKvhRkSNNb0NXDcXMXMevGh7jw9mXMuvGhwJtx5UXN4I9SrwK8TsYRvEqoXzGtIMchxHGCKt4w%0ADrxgDIauzsnicsso75sDTjvyrYE3y1P1TklLlKmTPYFvOedejrsxIvUuzjnwKBn81XYSQa9oyxXT%0AqiTuK+dyyY21LmZVOJIVZlqot39jpONduXA5V/92OYWxhd80WD1OJ0ljiBJo/C/wXmBFvE0RqW9J%0AzIGHTUqMo5O4p7u34jHjKKYVx5VzkMBu8SVTa7LcslIiZ7mdda+466nIxy0ewPALauttOkkaR5Sp%0Ak9nAKWb2AzP7jJn9S+FX3A0UqRdh9yBJQqUCXUHMW/ZSxWmNaotpQfVBUdAN44DEi1n5FdYqVKpQ%0AWP5xfeu3VDxG0Gb7TU/lc3+gPqaTpHFECTROB94PfBT4Z+Digq+L4muaSHaVmhfPwhx4uc4kqLXr%0At1QMhvIBTRRx7SqahcAOgidyhtlZt5QwKS1+r13VOyUNUaZO/g34CvCNXE0NkabilxNw2pFvDfT4%0ApOfAK1W3DKJSMFS4MqZS8a2k9r3IQmAH4RI5w+ysmzd+zHA+MmXvwHvcFCr12lW9U2otyojGCOAn%0ACjKkGZXbe+LKhcsZN3p4ovuKBDVjcgeLL5nK7BMmRXp8kGAoH9AUj2yMHzOc604/jBsSvnLOSnJj%0AlEDmlXWbAj/uyx86mGmdwXbsLeb32rOwN4o0jygjGj8ETgW+FnNbRDItSLJnXhZ2sBzWYhy735u4%0A5t7gedthEwJnTO5gcBC+NK9re55B3/qtXHHXU8yZ2ZloImZWkhujBDJhHpMvfR5mrxgldkqWRBnR%0AGAZ8zszuN7PvmNm3Cr/ibqBIVgTJCXhtw1YumnZAZubAwySHRgmGFnT18KlbhyYz5hMf8ytYkrhy%0AzkpyY9hzHGVn3TC5N0rslKyJEmgcAvwRb7+TycBhBV9T4muaSLYEHered8JoFl8yldvOPpqrT5vC%0AbWcfzeJLpqaSaBemgwobDAVd9RFnYa5iWUhuDHqOiwOAsIGS32stjiWU2ClZY84l959A1phZK9Df%0A399Pa2tr2s2ROrNkxVpm3fhQxfvddvbRmSvh7LfJ2qyj9mHfCWMiTWvU+nyUK+ue1LbnYZ67mjoa%0AYXZTLW7PEW/bncdWvxrra4/rfCb5vkjtDQwM0NbWBtDmnBsI+rhQgYaZ7QJsAqY457pCtzJlCjSk%0AGtsGHcfNXVQxJ2DxJVMz+Z9p3J3Hr7p6+NGS1RXvf/VpU6re1yTK1uZBX2+5+5U67vgxI/i3kyfz%0AwUPLBwFhKoNmqUMu/Zq9lS/TOtsDty3p7eil9moSaACY2QrgFOfc4+GamD4FGlKt/KoTKJ3s2ehD%0A1lG2Ma92RMOv+mc+4fasY/dlelEHGLSTK3c/oOzy3XOPn8ilH+yM/LqyKMgOskGChbufeIkLbv3j%0AkNub5e+kUdUy0PgE8DHgDOdcspVwYqZAQ+LQrFdqYbcxj2OEJz+KFCSwqRQgFHdylQKYcaOH53ag%0A9Xfd6YfxwUP3CvJSMi/oua4ULNz9RA+zb1vqW2As6yN/4i9qoBFleeu/APsBL5nZamB94S+dc4dH%0AeE6RutGMBY/CVrGMa+VDmGJYvf2bOO+WpYwbPbzifjNTD3xzxUTWSkEGeMt63z+5oyHe+6Dnuty+%0APQu6erjg1qUVH6/t6JtLlEDjjthbEYCZfRE4EW9lyxbn3Lg02iEC4Tc7q3dhtzGPa4fUMMWwggQI%0A+U7ux0tWRa6aWqhv/daG6TDDnuviYCEfjCZxPKlvoQMN59zlSTQkgBHAz4AlwCdTaoNIUwraKfzj%0AMW/jA5M7YhvhSaqq5+q+DbE9V6N0mFHOdeFrDxuMajv65hFlRAMAMzsCOAgvuO12zg3N/ImRc25O%0A7rhnJnkcERkqaKfwgckdsV7dh62IGdTbxo+O7bn8zk2WVpIEaU+Uc1342sMEXLUqxS/ZEDrQMLM9%0AgduB9wKv4U3XtZnZvcBpzrm/xNrCKpjZSGBkwU1j02qLSD1Lq9x34eZtxWXdo8i38x+O2ZfvL15Z%0A9vW0BUgG9esws5YwHKQ9hee6klLvd5gRClUtbS5RKoN+B2gFDnbOjXfO7Y5XIbQV+HacjYvBpUB/%0AwdcL6TZHpD6lWe7bryJmKQbbN7Yr184Ru7RUfD3fOOUQzj1+YtljlXrN5TbeO/+WpSzo6qn4OuIU%0Apj1+G+UV8nu/g5RibzFvpU4jr86SoaIsb+0HpjnnHim6/SjgN2GSNM3sMmBOhbsd6Zx7tOAxZwJX%0ABTmOz4jGC1reKhJNnFfqYacW8vdf2N1bcsv0wmWXQNV1NPL3u/uJl3Kbxm0t+1z5NpZbIlrrpZ1R%0A25M/1/d093LHspd22sum3PvtV2cm77rTDy9Z6EzqQy3raKwD3u2cW1Z0+2HA/c65wD24mU0AJlS4%0A2yrn3Pa/kjCBRonjqY5Gg8rafHgji+NcVxuwBHl8HJVBw77mrJWpj6M9Yd/vrE0bSXxqWUdjEXC1%0Amc1yzr0EYGZ7A1cCvw3zRM65NcCaCG0Q2U7/sdVWtUt7/Qpl5Yfyg1SNDFLLJGg7g9wv6HMFTYis%0A1UqVONoT9v1uxjozUl6UQGM2MA9YZWbP442Q7QM8CZwRY9t2Ymb7AONzxxpmZvmdYp9xzr2e1HEl%0A2+LotKR2Ku346lcIqpSoAU+So19BEyJrtbQzrfY0W50ZKS9KHY3ngcPNbDpwIN7/Dd3OuYVxN67I%0AV4GPF/ycX057AnBfwseWDIqz05LkFHbsa9ZtLltrIemqkdWOflW7RDSp1Tl+stYeaU6R62g45+4B%0A7omxLZWOdyZwZq2OJ9lXqUCQSh2nL8ombJDM1EK1o19hl4gWL8dNenVOKVlrjzSnKMtbMbP3mdnX%0AzOz7ZvbfhV9xN1DET9bmw2Vnfssqg4h7KL/S6Bd4o1/bfHYCi7JEtHg5bnvbqFSm8rLWHmk+UQp2%0AzQG+AjwK9FB9DR2RSLI2Hy47hN2ELS+pofxqRr+iTNGlmRBZanpHCZqSpihTJ+cBZzrnfhx3Y0TC%0A0PxzdEkvBw6770WhJIbyqxn9ihqkpJEQWWl6R1OIkoYogcYI4PdxN0QkLM0/R1OL5cBRp6vOOX5i%0AIkP51Yx+1csUnVZgZYNq+gwVJUfj+8DpcTdEJArNP4dTq/LYUaarDLjz8R7fPIlqVCqPbfjvW1IP%0AU3TV5qBIPBZ09XDc3EXMuvEhLrx9GbNufIjj5i6qedn5rIkyojEKOMfMpgFPADvtOuSc+3QcDRMJ%0ASvPPpRVfWR3xtt1rthw4yk6gSa4Sqmb0qx6m6LQCK30aUfIXJdA4FMiXH59c9DuFy5IKFQjaWanp%0AkfFjhu+0X0exODujanZdTWoKIj/6VXxe2itMG9XDFF29TO80KtX0KS9Kwa4TkmiIiMTD78qqXJBR%0AKK7OyK9jryTJKYioo19Rg5RaqYfpnUamEaXyIhfsEpHsibqstFCcnVFhx947sIkr/u9PvgFPraYg%0Aoo5+ZXmKrh6mdxqZRpTKU6Ah0kCqWVaaVGdU2LHvOryl5DbiWZmCqCSrU3T1ML3TyDSiVF6kyqAi%0Akk1Rr5hq1RlplVBydG7TU82qpmagEQ2RBhL0imn8mBH0rd+y/eda5hpkeQqiFoLUWYhai6HZz21a%0AsjSilMU6HuZc8ywUMbNWoL+/v5/W1ta0myMSu22DjuPmLqo4V3//Z0/gsdWvZuo/o2YQpFhaNQXV%0AstjJNJNaFMNL8/gDAwO0tbUBtDnnBoI+ToGGSIPJrzqB0ldWGkZPh99qoML3Bah4H7/3Lu1OTjxp%0ABXtBPl/Vfg4UaASgQEOahTqdbMmPNPkl6hrw5taRgNE74H+f9rZRLL5k6pCOqxadjGRXkM+X32cn%0AjKiBhnI0RBqQ5uqzJUidhd6BzWWfw68Wg4pFSdbreCjQEGlQWV2K2YzirJ9Q/FxpdTLKB8mOrNfx%0AUKAhIpKwOOsnFD9XGp2MpuayJet1PFRHQ0Qkgm2DjiUr1jJv2YssWbG27M6oQeostLeOpL01fC2G%0AWncytdoBWILLeh0PjWiIiIQU9oo+SJ2Fy046GKDsfb58YueQ6Ypalh9XPkg2ZamORyladSIiEkI1%0AKzyqqaNx0js6uPPxnpKPBWqypHnJirXMuvGhive77eyjlR+UAtXRyAAFGiJSjTiWEUapDPrq+s18%0A6tY/VqzBkXTexLxlL3Lh7csq3u/q06Zw8pS9YzmmhJNkkq6Wt4qIJCyOFR5BVgMV3icf3FSarlh8%0AydTElzRnPelQsrnaTIGGiEhAaazwCBvcJNnJaDt6iUKrTkREAkrjij5LNRLySYfAkBUOWUg6lGxS%0AoCEiElAtlhEWL5udMGZkoMfVarpC29FLWJo6EREJKMwywihJeaVWDbS3jmLc6OH0b9iamekKlbiX%0AMLTqREQkpErLCKMsMyy3bNaV+D7/MwRbvqqS4VItLW8NQIGGiMTFr+OOUmcjyLLZcaOHM3KXlp02%0AXwu6fFUlwyUOCjQCUKAhIkmKWmcjaCGs//mnv6bFLPR0jLaQlziojoaISMqi1tkIumJkzeubQxXC%0AUsnw+GjqKToFGiIiMYm6FDWpZbNpbSHfaDT1VB0tbxURqULhctQ16zZXfgAMWbKa1LLZ3oHs1OCo%0AV9qttnoa0RARiajUlW6LQZkd4wH4zM8e57KTdlwNJ7H75oKuHq74vz8Fuq9Khpemqad4aERDRCQC%0AvyvdSkEGwMsDQ6+G4yyElW9b3/qtZe8XR4GxRhZm6kn8aURDRCSkcle6ecUjE4X8robjKIQVpG35%0A9oFKhpeTpfLv9UyBhohISJWudME/yCj8falEzGp33wzSNoDxY0bw7x+ZrGTGMoJOKa1Zt5ltg04B%0Am4+6mDoxs33N7CYzW2lmG81shZldbmYj0m6biDSfOK9g474aDvp8XzrxIAUZFVRK0s274q6nOG7u%0AIiWG+qiLQAM4EK+t5wIHAxcD5wFfS7NRItKc4kyejDsRM+jztbftGutxG1G53WqLaRWKv7oINJxz%0AC5xzn3DO/cY596xz7k7gP4FT0m6biDSfIMtR21tH0t6a7E6vUdumBNDg/JJ0i+Wnyi6f3822IBnB%0ATaQuAg0fbUDZVF8zG2lmrfkvYGxtmiYijazclW7+58tOOpjLTip/nyQSMYO0TQmg4cyY3MHiS6by%0A5RMPKns/rUIprS4DDTObBPwzcEOFu14K9Bd8vZBw00SkSQRZjhrnktW42ybhDGsxJowdWfmOaBVK%0AsVQ3VTOzy4A5Fe52pHPu0YLH7AXcD9zvnPunCs8/Eij8ZIwFXtCmaiISlyB7YKS1T4b254hX0M3v%0Abjv76IYs6V6Xu7ea2QRgQoW7rXLObcrdfy/gXuAPwJnOucGQx9PurSIiEkl+d97e/k0lly/77c7b%0AKOpy91bn3BpgTZD7mtneeEHGY8AnwgYZIiIi1UiiVHwzqIscjdxIxn3A88C/Am8ys3Yza0+1YSIi%0A0lSU/xJeqlMnQZnZmcDNpX7nnAscOmrqRERE4tCM+S91maNRawo0RER2aMbOUqKryxwNERFJR6kt%0A7jvaRjFnZqeG/yVWdZGjISIi8fHb4l5ltCUJCjRERJpIuW3kVUZbkqBAQ0SkiVTaRl5ltCVuCjRE%0ARJpI0PLYKqMtcVGgISLSRIJuIx/39vXSvBRoiIg0EW0jL7WmQENEpIloG3mpNQUaIiJNRmW0pZZU%0AGVREpEmpMqiEocqgIiISyrAW45hJe6TdDGlwmjoRERGRxCjQEBERkcQo0BAREZHEKNAQERGRxCjQ%0AEBERkcQo0BAREZHEKNAQERGRxKiOhoiEoiJPIhKGAg0RCWxBVw+Xz++mp3/HFuIdbaOYM7NTZatF%0ApCRNnYhIIAu6ejj/lqU7BRkAvf2bOP+WpSzo6kmpZSKSZQo0RKSibYOOy+d3U2pnpPxtl8/vZttg%0A8+ydJCLBKNAQkYoeXtk3ZCSjkAN6+jfx8Mq+2jVKROqCAg0RqeiVdf5BRpT7iUjzUKAhIhXtOXZU%0ArPcTkeahQENEKjpq4ng62kbht4jV8FafHDVxfC2bJSJ1QIGGiFQ0rMWYM7MTYEiwkf95zsxO1dMQ%0AkSEUaIhIIDMmd3D9GYfT3rbz9Eh72yiuP+Nw1dEQkZLMueZZjmZmrUB/f38/ra2taTdHpC6pMqhI%0AcxoYGKCtrQ2gzTk3EPRxqgwqIqEMazGOmbRH2s0QkTqhqRMRERFJjAINERERSYwCDREREUmMAg0R%0AERFJjAINERERSYwCDREREUlMUy5vHRgIvPxXREREiN53NlvBrr2BF9Juh4iISB17i3PuxaB3brZA%0Aw4C9gHUJH2osXkDzlhocK+t0LnbQudhB52IHnYud6XzskMVzMRZ4yYUIHppq6iR3YgJHYVF58QwA%0A68KUaW1EOhc76FzsoHOxg87FznQ+dsjouQjdDiWDioiISGIUaIiIiEhiFGgkYzNwee7fZqdzsYPO%0AxQ46FzvoXOxM52OHhjgXTZUMKiIiIrWlEQ0RERFJjAINERERSYwCDREREUmMAg0RERFJjAKNhJnZ%0AnWb2nJltMrMeM/uxme2Vdrtqzcz2NbObzGylmW00sxVmdrmZjUi7bWkwsy+a2e/NbIOZvZZ2e2rN%0AzC7IfRY2mdljZvbutNuUBjM73szmm9lLZubM7MNptykNZnapmT1iZuvM7BUzu8PM3p52u9JiZueb%0A2RNmNpD7WmJmH0i7XVEp0EjevcDfAW8HPgpMAv431Ral40C8z9u5wMHAxcB5wNfSbFSKRgA/A65P%0AuyG1ZmanAlcB/w4cBvwO+JWZ7ZNqw9IxBngcmJ12Q1L2HuBa4GhgOl7V6t+Y2ZhUW5WeF4DPA+/M%0AfS0C5pnZwam2KiItb60xMzsJuAMY6ZzbmnZ70mRmnwXOd879VdptSYuZnQlc5Zwbl3ZbasXM/gAs%0Adc6dX3DbU8AdzrlL02tZuszMAR9xzt2RdlvSZmZvAl4B3uOceyDt9mSBmfUBn3XO3ZR2W8LSiEYN%0Amdl44O+B3zd7kJHTBvSl3QipndxU2RHAb4p+9RvgXbVvkWRUW+7fpv//wcyGmdlpeKNfS9JuTxQK%0ANGrAzOaa2XpgLbAPcHLKTUqdmU0C/hm4Ie22SE1NAIYBLxfd/jLQXvvmSNbkdtn+FrDYOdeVdnvS%0AYmaHmNnreFVBb8Ab7ePQbU0AAAioSURBVOpOuVmRKNCIwMwuyyVulft6Z8FD/gNvLvpvgG3Aj6xg%0AW756FuFckEuGXQD8zDn3/XRaHr8o56KJFc/ZWonbpDldAxwKzEq7ISn7MzAFL2/leuCHZtaZbpOi%0Aaapt4mN0DXB7hfusyn/jnFsDrAGezs1FP4/34anLYbAioc5FLsi4F++1n5Ncs1IR6lw0qTV4wXbx%0A6MWeDB3lkCZjZt8BTgKOd869kHZ70uSc2wI8k/vxUTM7ErgQL6G+rijQiKAgcIgiP5IxMqbmpCrM%0AuTCzvfGCjMeATzjnBpNsW61V+bloCs65LWb2GN7Kgl8W/Go6MC+dVknaciO83wE+ArzXObcy5SZl%0AkVGn/YYCjQSZ2VHAUcBi4FXgr4CvAitojNGMwHIjGfcBzwH/CrwpP3vknOtNr2XpyC3lHI+XszPM%0AzKbkfvWMc+719FpWE98Cfmxmj7JjZGsfmjBfx8x2A/YruGli7rPQ55x7LqVmpeFa4HS8/LV1ZpYf%0A8ep3zm1Mr1npMLOvAb/CG/0eC5wGvBeYkWKzItPy1gSZ2SHA1cA78DKGe/ByE/7NOfdimm2rtdwy%0AzptL/c451xD5KmGY2Q+Aj5f41QnOuftq25raM7MLgM8BHUAXcHEzLmM0s/fijfIV+6Fz7szatiY9%0AuaW9pXzCOfeDWrYlC8zsJuB9eH8f/cATwFzn3D2pNiwiBRoiIiKSGK06ERERkcQo0BAREZHEKNAQ%0AERGRxCjQEBERkcQo0BAREZHEKNAQERGRxCjQEBERkcQo0BAREZHEKNAQkcDM7AdmdkfBz/eZ2VUJ%0AH9OZ2YdDPmandpnZKjO7KP7WiUgl2utERKpxCrA17UYEcCSwPsgdzWwVcJVzLtEASqRZKNAQaSBm%0ANtw5V7OO3znXV6tjVcM595e02yDSrDR1IpKS3PD+t83sm2bWZ2a9ZnZZ0X32MbN5Zva6mQ2Y2U/N%0A7M0Fv7/MzJaZ2Vlm9iyw2Tz3mdl3zOwqM3vVzF42s3PMbIyZ3Wxm68xshZl9oOC5hpnZTWa20sw2%0AmtmfzezCAK/hqtz3781NcxR//aDg/jPN7DEz22Rmz5rZHDPbpeD3+5vZA7nfd5vZ9ADncYyZ/Sh3%0AjnrM7DMl7rPT1EnuvD1nZpvN7CUz+3b+9QBvA67Mtz93+x5mdpuZvWBmG8zsSTObVeJcVHo/x5nZ%0A93LvxyYz6zKzDxX8/l2517/RzJ7PPd+YSudAJMsUaIik6+N4Q/p/jbeb6VfynauZGXAH3nby7wGm%0AA5OAnxQ9x37A3wEfBaYU3P5xYA1wFPAd4HrgZ8DvgcOBX+Nt1z46d/8W4IXcc3UCXwW+ZmZ/F/C1%0A/B5vt8n811RgE/BA7vW8H7gF+Hbu+c8FzgS+mPt9C/ALYBtwNHAeMDfAcf8DOAH4CPA3eNtpH+F3%0AZzP7W+Di3PH3Bz4MPJn79Sl45+ArBa8DYBTwGPAhYDLwPbxz99dFT1/u/WzB2/r7XcAZuXPw+dzr%0Aze/2/OvcOTgUOBU4DrgmwDkQyS7nnL70pa8UvoD7gN8V3fYw8I3c99OBN4C3Fvy+E3DAkbmfLwO2%0AAG8q99zAMOB14EcFt7XnnuvoMm28Fvjfgp9/ANxRdJyrSjxuD+AZ4NqC2x4ALi263xnAS7nv/yb3%0Aet9S8PsZuTZ+2Kd9uwGbgVMLbhsPbChsF7AKuCj3/aeBPwPDfZ5z+30rvH93Af8Z4v38G7yg4gCf%0A5/sR8N2i247LPWZU2p9Xfekr6pdyNETS9UTRzz3AnrnvDwKed849n/+lc67bzF7L/e6R3M2rXekc%0AhCcKHrfNzNay48od4OXcv/njYWbnAf+EN32wKzACWBbmBZnZcODnwHNA4dTLEcCRZvbFgtuGAaNy%0AoyoHAc85514o+P2SCoeblGvj9vs55/rM7M9lHvMz4CLgWTNbANwNzHfOvVHmNQ3DG304FdgbGJn7%0AKk4wLfd+TgFecM497XOYI4D9zOzvCw+NN9I0EXiqzGsSySwFGiLpKk7cdOyY0rTcz8WKb/dbTVHq%0Aubff5pxz3uyMd7zcFMmVwGfwOu51wGfxpgHCuB7YB2/UpbDzbgHm4E0NFNuE97qKlXr9hUo9pizn%0A3PNm9na8EaNpwHXAZ83sPc4/kfYzeNMtF+EFa+uBq/CCnELl3s+NFZrWAnwXb2qp2HMVHiuSWQo0%0ARLKrG9jHzN6aH9Uws06gjWSubt8N/N45d13+BjObFOYJzOzTeFf9xzjn1hb9einwdufcMz6Pzb/e%0AvZxzL+VuPqbCIZ/B69yPJtcZm9nuwAHA/X4Pcs5tBO4E7jSza4H/BxySa+MWvJGWQu8G5jnnbskd%0AowUvvyPM+/AE8BYzO8BnVGMpcLDf+RGpVwo0RLJrIV7n9D+5FRO74F193++cezSB4z0D/GMuaXMl%0A8A949SdWBnmwmU0Dvgl8ClhjZu25X210zvXjJZf+n5k9jzd9MYiX9HiIc+5LeK/3z8CPcitHWoF/%0AL3dM59zrZnYT8B+5qaGXc48ZLNPOM/ECiT/g5XL8A95ow+rcXVYBx5vZ7cBm59ya3Ln5qJm9C3gV%0AL8+jnRCBhnPufjN7APh5LiB7BjjQ+5VbgJf4+lAu8LkRb9TkIGC6c+6fgx5HJGu06kQko5xzDm9F%0AxKt4iZQLgWfxRgyScAPetMZP8DrhPfACm6COw+vAb8DLTch/XQ3gnPs13qqN6Xj5JQ/hddirc78f%0AxFs5MhIvifL75FakVPBZvPNzJ945Woy3QsTPa8DZwIN4gdz7gJkFIzBfAfYFVgD53Jcr8EYcfo2X%0A9NmLtyIorI/ivfbb8Easvklu9MQ59wTe6qL9gd8Bf8wdtyfCcUQyw7z/y0RERETipxENERERSYwC%0ADREREUmMAg0RERFJjAINERERSYwCDREREUmMAg0RERFJjAINERERSYwCDREREUmMAg0RERFJjAIN%0AERERSYwCDREREUnM/wevPMtUOLrtSQAAAABJRU5ErkJggg==" alt="" />
Shape of the series: (197,)
Shape with newaxis: (197, 1)
-0.607598822715
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAiIAAAFdCAYAAAA+KAajAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz%0AAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBo%0AdHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzs3Xd8leX9//HXJ5tAEjYBwhQIU0Bk%0AOgAV1FrbL25FBeserbOuWqv9abXWVbW2ghUVdxWpC8WJg43sPcImbBLIHtfvj/sET2MYGXCfc/J+%0APh73w5z7vs593kdEPlz3Ncw5h4iIiIgfovwOICIiIrWXChERERHxjQoRERER8Y0KEREREfGNChER%0AERHxjQoRERER8Y0KEREREfGNChERERHxjQoRERER8Y0KEREREfGNChERERHxTYzfAUKJmRnQAtjr%0AdxYREZEwlARsdpXYyE6FyP9qAWz0O4SIiEgYSwM2HW5jFSL/ay/Ahg0bSE5O9juLiIhI2MjOzqZV%0Aq1ZQyacKKkQqkJycrEJERETkKNBgVREREfGNChERERHxjQoRERER8Y0KEREREfGNChERERHxjQoR%0AERER8Y0KEREREfGNChERERHxjQoRERER8Y0KERERkVpm9fZ95BeV+B0DUCEiIiJSqzjnuHb8HAY8%0A8iVz1u3yO44KERERkdpkZsYuVm3bR2FxKZ2aJfkdR4WIiIhIbfL6jPUA/LpXC5ISYn1Oo0JERESk%0A1ti5r4BPF2UCcEm/Nj6n8agQERERqSXenbORwpJSjk1LoUdait9xABUiIiIitUJpqeONmd5jmZH9%0AW/uc5icqRERERGqBH1bvYN3OXJLiYzi7Zwu/4+ynQkRERKQWeCMwSPWc41qSGBfjc5qfqBARERGJ%0AcFuz85m8ZCsAl/QPjUGqZVSIiIiIRLh3Zm2gpNRxfJsGpKf6v3ZIMBUiIiIiEayk1PFm2SDVAaEz%0ASLWMChEREZEI9s3ybWzOyqd+Yixndm/ud5yfUSEiIiISwcZPXwfA+X3SSIiN9jnNz1WqEDGzB8zM%0AlTsyg65boM1mM8szs2/MrFu5ezQws/FmlhU4xptZ/aDr6Wb2tZltNbN8M1tjZg+Z2UHXoa0glzOz%0A6yrz/URERCLJup05TFmxHYCRITZItUxV5u8sBk4Leh28j/CdwG3AaGAFcB/wuZmlO+f2Btq8AaQB%0AZwRejwHGA2cHXhcBrwI/AnuAnsBYvKLp3kNkuwL4NOh11uF+KRERkUjzxoz1OAcnd2pC28Z1/Y5T%0AoaoUIsXOuczyJ83MgFuAh51zEwLnRgFbgUuAF8ysC14BMsA5NyPQ5mpgWqBYWe6cWwOsCbr1OjMb%0AApx0GNn2VJRNRESktskvKuGd2RsAuGxAaPaGQNXGiHQMPHrJMLO3zKx94Hw7IBWYXNbQOVcATAEG%0ABU4NBLLKipBAm+l4PRdlbf6HmXXAK16mHEa258xsh5nNMrPrzOyg38/M4s0suewAQmtOk4iISBV9%0AsnALu3OLaFm/Dqd0bup3nAOqbCEyA7gcOB24Gq/wmGpmjQI/g9cDEmxr0LVUYFsF990W1AYAM5tq%0AZvnASuA74P5DZPsjcD7eY6O3gCc49KOce/CKoLJj4yHai4iIhIWyQaqX9G9NdJT5nObAKvVoxjk3%0AKejlQjObBqwGRgHTy5qVe5uVO1f+ekVtAC7E66HoCfwNuAN47CDZHgp6Oc97UsT9wEMVvwOAR4An%0Ag14noWJERETC3KJNWcxdv4fYaOOC41v5HeegqrXYvHMux8wWAh2BiYHTqcCWoGZN+amXJBNoVsGt%0AmlCuJ8U5tyHw4xIziwbGmNkTzrmSn727YtOBZDNr5pwr30tT9hkFQEHZ60DxIiIiEtZeC/SGnNm9%0AOU2S4n1Oc3DVWkfEzOKBLniFRwZeoTEs6HocMBiYGjg1DUgxs35BbfoDKUFtKvwoIDbwz8PVG8jH%0Am3kjIiJSK2TlFTFx3iYALg3hQaplKtUjYmaPAx8C6/F6Ou4DkoFXnHPOzJ4G7jWzlXhjO+4FcvGm%0A7OKcW2pmnwJjzezawG3HAB8555YHPmMk3hTehXi9FX3wHqG87ZwrDrQZATzinOsceH02Xk/MNCAP%0AGAo8DIwJ9HqIiIjUCu/N2Uh+USnpzZLo27aB33EOqbKPZtKAN4HGwHa8xx8DnHPrAtcfA+oAzwMN%0A8Aa3Dg9aQwRgJPAMP82u+QC4Keh6MXAX0AmvB2Qd8A/gqaA2KUB60Osi4Aa88R5ReNN/7w+8T0RE%0ApFYoLXX7B6leOrBNWAw5MOcqGjtaOwWm8GZlZWWRnJzsdxwREZFKmbJiO6NemklSfAzT7z2VuvHV%0AGgpaKdnZ2aSkpACkOOeyD/d92mtGREQkQrw6dS0A5x2fdlSLkOpQISIiIhIB1u/M5avl3lJdobyS%0AankqRERERCLAazPW7d9Xpn2Ten7HOWwqRERERMJcXmEJb8/ylt8aNTB8ekNAhYiIiEjY+2D+JrLy%0AimjVsA5D0kN3X5mKqBAREREJY845XpnqTdm9bECbkN5XpiIqRERERMLYnHW7WbIlm/iYqJDfV6Yi%0AKkRERETC2CvTvN6Q/+vVkvqJcT6nqTwVIiIiImEqMyufSQu9fWYvC7NBqmVUiIiIiISp12eso7jU%0A0a9tQ7q3TPE7TpWoEBEREQlD+UUlvDFjPQBXnNDW3zDVoEJEREQkDH04fzM7cwppkZLAsK7N/I5T%0AZSpEREREwoxzjpcD+8pcNrAtMdHh+8d5+CYXERGppWav283izdkkxEZxUd/wm7IbTIWIiIhImBn3%0AQwYAI3q3pEHd8JuyG0yFiIiISBjZtCePzxZvBWDUoLb+hqkBKkRERETCyGvT11FS6hjYvhGdU5P9%0AjlNtKkRERETCRF5hCW/O9Kbsjg7jKbvBVIiIiIiEiffnbmJPbhFpDepwWpfwnbIbTIXIEeScY/Li%0ATC4ZO52t2fl+xxERkTDmnOOlwCDV0YPaht0uuweiQuQIMjPGfreGqat38uq0tX7HERGRMPbtyh2s%0A2raPevExXBjmU3aDqRA5wq48sR0Ar89YT15hic9pREQkXP37e6835ILjW5GUEOtzmpqjQuQIG9Y1%0AlVYN67Ant4gJczf6HUdERMLQyq17+XbFdsy8xzKRRIXIERYdZYwe5PWKvPR9BqWlzudEIiISbl76%0AYS0Aw7s2o3WjRH/D1DAVIkfBBcenUS8+htXbc5iycrvfcUREJIzsyilkwo9ej/qVJ7b3OU3NUyFy%0AFCQlxO7fC+Df32X4nEZERMLJmzPXU1BcSveWyfRt28DvODVOhchRMmpQW6IMvl+1g2WZ2X7HERGR%0AMFBYXMorgV12rzyxHWaRMWU3mAqRo6RVw0TO6J4KeGNFREREDuXjhZvZtreApknxnNWjhd9xjggV%0AIkdR2VTeifM2s2Nfgc9pREQklDnnGPut9xfXUYPaEhcTmX9kV+pbmdkDZubKHZlB1y3QZrOZ5ZnZ%0AN2bWrdw9GpjZeDPLChzjzax+0PV0M/vazLaaWb6ZrTGzh8zsoJOmzay1mX1oZjlmtsPMnjGzkNob%0A+bjWDejZqj6FxaWMn7bO7zgiIhLCpq3eyZIt2dSJjWZk/9Z+xzliqlJeLQaaBx09gq7dCdwG3AT0%0ABTKBz80sKajNG0Av4IzA0QsYH3S9CHgVGA6kA7cAVwMPHiiQmUUDHwN1gROBi4BzgSeq8P2OGDPj%0AqkCvyGvT15FfpAXORESkYmO/WwPA+cenUT8xpP5eXaNiqvCeYudcZvmT5o2guQV42Dk3IXBuFLAV%0AuAR4wcy64BUfA5xzMwJtrgammVm6c265c24NsCbo1uvMbAhw0kEyDQe6Aq2cc5sD970deNnM/uCc%0AC5nRoWd2T6Vl/Tps2pPHhB83cUkEV7kiIlI1q7bt5evl3gJmvzmhnd9xjqiq9Ih0DDx6yTCzt8ys%0AbFJzOyAVmFzW0DlXAEwBBgVODQSyyoqQQJvpQFZQm/9hZh3wipcpB8k0EFhUVoQEfAbEA30q8+WO%0AtJjoKH4T6BV58bs1WuBMRER+5sXAUg/DuzajbeO6Pqc5sipbiMwALgdOx3tckgpMNbNGgZ/B6wEJ%0AtjXoWiqwrYL7bgtqA4CZTTWzfGAl8B1w/0FypZb/XOfcbqCw/H3LfUa8mSWXHUDSgdrWpAv7tiIp%0AIYY1O3L4allF/zpERKS22r63gAlzNwFw9UmRt4BZeZUqRJxzk5xz7znnFjrnvgDOClwaFdys3Nus%0A3LmKugDKtwG4EDgO77HOWcAdh4p3mPcNdg9eb0zZcVQ2g6kXH7P/kcyY79YcorWIiNQm46evo7C4%0AlF6t6tOnTeQtYFZeteYCOedygIVAR7yBqfDzHoim/NRbkQk0q+BWTfh5j8YG59wS59ybwN3AA4FB%0AqRXJLP+5ZtYAiC1/33IeAVKCjrSDtK1RVwxqR0yUMTNjF/M27DlaHysiIiEsv6iE16Z7syqvPql9%0ARC5gVl61ChEziwe6AFuADLyCYFjQ9ThgMDA1cGoakGJm/YLa9McrAsraVPhReEXFgX5FpgHdzax5%0A0LnhQAEw50A3dc4VOOeyyw5g70Ey1KjUlAR+1ctbnGasekVERAR478eN7MopJK1BHU7vVtHf2yNP%0AZdcRedzMBptZu0AB8S6QDLzinHPA08C9ZjbCzLoDLwO5eFN2cc4tBT4FxprZADMbAIwFPnLOLQ98%0Axkgzu8DMuphZezM7H6/n4m3nXHGgzQgzWxYUbTKwBBhvZr3N7FTgcWBsKM2YKe+qwOZFkxZuYcOu%0AXJ/TiIiIn0pK3f5Bqr85oR0x0ZG5gFl5lf2WacCbwHJgAt5g0AHOubLVuR7DK0aeB2YDLYHhzrng%0AnoaReI9zJgeOBcBlQdeLgbuAmYFrDwD/AK4KapOCt8YIAM65ErxxJPnAD8A7wEQOPa7EV11bJHNS%0Ax8aUOnjpBy37LiJSm32+JJOMHTmk1InlwsBGqbWBeR0ZAhCYOZOVlZVFcnLyUfnMb1ds5/KXZpIY%0AF83Uu0+J6EVrRESkYs45Rjw/lXkb9nDT0A7ccXr6od8UYrKzs0lJSQFIqczTiNrR7xPCTurYmM6p%0ASeQW/jRASUREapdZa3czb8Me4mKiGDWord9xjioVIj4zM64bfAwAL09dq2XfRURqoRemrAbgvD5p%0ANEmK9znN0aVCJAScdWxzWtavw459hbw756gsZSIiIiFi5da9fLlsG2a1YwGz8lSIhIDY6CiuOslb%0A9n3sd2so0bLvIiK1xphvvSUcTu+aSrsIX869IipEQsSFfVtRPzGWdTtz+Wzxz/YUFBGRCJSZlc/E%0Aed5y7tcMrn29IaBCJGQkxsVw+cC2gPesULOZREQi37gfMigqcfRr25DjWkf+cu4VUSESQkYNbENC%0AbBTzN2Yxbc1Ov+OIiMgRlJ1fxBsz1gNwzcm1szcEVIiElEb14rngeG8RmxemaNl3EZFINn7aOvYW%0AFNOpWT1O6dzU7zi+USESYq46sT1RBlNWbGfJ5pBdnV5ERKohv6iEcYEVta8bfAxRUZG/ud2BqBAJ%0AMa0bJXLWsd5meP8MzCsXEZHI8p85G9mxr5CW9etwds8WfsfxlQqREHR9YIGzjxdsZu2OHJ/TiIhI%0ATSouKWXMt95fNK85uT2xtWRzuwOp3d8+RHVtkczQ9CaUOnjhW40VERGJJB8v3MKGXXk0rBu3f1xg%0AbaZCJERdP6QDAO/N2cjW7Hyf04iISE1wzvHPb7zekCsGtaVOXLTPifynQiRE9WvXkOPbNKCwpJR/%0Af5/hdxwREakB3yzfzrLMvdSNi96/dlRtp0IkhN0w1Bsr8vr0dWTlFvmcRkREqqusN2TkgDakJMb6%0AnCY0qBAJYUPTm9I5NYmcwhJembbW7zgiIlINs9buYubaXcRGG785oZ3fcUKGCpEQZmZcP8TrFRn3%0AQwa5hcU+JxIRkap67qtVAJzXJ43UlASf04QOFSIh7qwezWndMJHduUW8NXOD33FERKQKFm7MYsqK%0A7USZt4CZ/ESFSIiLiY7a/x/tmG/XUFBc4nMiERGprH987fWG/KpnC9o0qutzmtCiQiQMnNunJanJ%0ACWRm5/PenE1+xxERkUpYuXUvny7OBOCGoR18ThN6VIiEgfiY6P07Mz7/zSqKSkp9TiQiIofr+cBM%0AmdO7NaNTsySf04QeFSJh4uJ+rWlUN46Nu/P4YN5mv+OIiMhhWLczh//O83qybxra0ec0oUmFSJio%0AExfNVSd5vSL/+GYVJaXO50QiInIo/5qymlIHJ3dqQo+0FL/jhCQVImHk0gGtSakTy5rtOXy6KNPv%0AOCIichBbsvJ4d85GAG7S2JADUiESRpISYrnihLYAPPvVSpxTr4iISKh6Ycoaikoc/do2pF+7hn7H%0ACVkqRMLM6EFtqRsXzbLMvXy5dJvfcUREpALbsvN5c+Z6AH53qsaGHIwKkTBTPzGOywIbJalXREQk%0ANHnrPpVyXOv6nNChkd9xQpoKkTB01UntSIiNYv7GLL5Zsd3vOCIiEmTHvgJem7EO8HpDzMznRKFN%0AhUgYalwvnkv7twHg71+oV0REJJSM/W4N+UWl9ExLYXCnJn7HCXkqRMLUNYPbEx8TxbwNe/hu5Q6/%0A44iICLArp5Dx09QbUhmVKkTM7AEzc+WOzKDrFmiz2czyzOwbM+tW7h4NzGy8mWUFjvFmVj/o+hAz%0A+6+ZbTGzHDObZ2YjDyNb+VzOzK6rzPcLJ02TEhhZ1ivypXpFRERCwUvfZ5BbWEK3Fsmc0rmp33HC%0AQlV6RBYDzYOOHkHX7gRuA24C+gKZwOdmFrym7RtAL+CMwNELGB90fRCwADgXOBZ4CXjVzM4+jGxX%0AlMv2SiW/W1i5bnB74mKimLNuNz+s2ul3HBGRWi0rt4iXp64F1BtSGTFVeE+xc+5nq2mZ92/8FuBh%0A59yEwLlRwFbgEuAFM+uCV3wMcM7NCLS5GphmZunOueXOub+Uu/UzZnY6MAL48BDZ9lSULVI1TU7g%0Akn6teXnqWv7+5QpO6NBI/+GLiPjk3z9ksK+gmM6pSQzr0szvOGGjKj0iHQOPXjLM7C0zax843w5I%0ABSaXNXTOFQBT8Ho5AAYCWWVFSKDNdCArqE1FUoBdh5HtOTPbYWazzOw6Mzvo9zOzeDNLLjuAsNuN%0A6LrBxxAXHcWstbuZtka9IiIifsjKLWLc9xkA/PaUjkRF6S+Fh6uyhcgM4HLgdOBqvMJjqpk1CvwM%0AXg9IsK1B11KBilbh2hbU5n+Y2Xl4j3nGHSLbH4HzgdOAt4AngHsP8Z578IqgsmPjIdqHnNSUBC7q%0A1wrwZtCIiMjR9+/v17A30BtyZvcK/ziTA6hUIeKcm+Sce885t9A59wVwVuDSqOBm5d5m5c5VNKqy%0AfBvvpNkQ4GXgaufc4kNke8g5N805N8859wRwP/D7g70HeASvt6XsSDtE+5BU1isyI2MXU1drBo2I%0AyNG0J7eQl35YC8DNp6o3pLKqNX3XOZcDLAQ64g1MhZ/3bDTlp16STKCiB2dNKNeTYmaD8caE3Oac%0Ae7UK8aYDyWZ2wAd1zrkC51x22QHsrcLn+K5F/Tr7e0We/lwzaEREjqax363ZPzbk9G7qDamsahUi%0AZhYPdAG2ABl4hcawoOtxwGBgauDUNCDFzPoFtemP1xsxNejcEOBj4G7n3JgqxusN5AN7qvj+sHLD%0AkA7ExUQxc+0uzaARETlKduUU8nKgN+SW0zqpN6QKKruOyONmNtjM2gUKiHeBZOAV5/01/GngXjMb%0AYWbd8R6r5OJN2cU5txT4FBhrZgPMbAAwFvjIObc88BlD8IqQZ4D3zCw1cDQMyjHCzJYFvT7bzK42%0As+5mdoyZXQU8DIwJDJiNeKkp3gwagCc/X65eERGRo2Dsd2vIKSyha/NkTu+mmTJVUdkekTTgTWA5%0AMAEoxJuKuy5w/TG8YuR5YDbQEhjunAt+5DES73HO5MCxALgs6PpoIBFvIOmWoGNCUJsUID3odRFw%0AA16PywLgZrwxIrdX8vuFtRuGHEN8TBQ/rt/DFO1BIyJyRO3cV8ArgXVDbjlN64ZUlelvzj8JTOHN%0AysrKIjk52e84VfLQR0t48fsMeqalMPHGE/QbQ0TkCHlk0lJemLKG7i2T+fCmE2v9/2+zs7NJSUkB%0ASAmMuzws2msmwlw7+BjqxEYzf2MWXy+vaKa0iIhU1/a9Bbw61XsYcMupnWp9EVIdKkQiTJOkeC4f%0A6O1B8+TnKzRWRETkCPjnN6vJKyqhZ6v6nNpFe8pUhwqRCHTNye1JjItm0aZsPltcfn05ERGpji1Z%0Aebw2w+sNuWO4ekOqS4VIBGpUL54rTmgLwFOfr6CkVL0iIiI15dmvVlFYXEq/dg05sUNjv+OEPRUi%0AEeqak44hKSGG5Vv38uH8zX7HERGJCOt35vLOrA0A3D5MvSE1QYVIhEpJjOXak739CJ/6YgVFJaU+%0AJxIRCX9//3IlxaWOkzo2pn/7Rn7HiQgqRCLYFSe0o1HdONbtzOXdOWG3n5+ISEhZtW0f78/1/l96%0Ax/D0Q7SWw6VCJILVjY/h+iHHAPDMlyvJLyrxOZGISPh66osVlDoY1rUZPVvV9ztOxFAhEuEuHdCG%0A5ikJbMnK540Z6/2OIyISlhZvzuLjBVsAuG1YJ5/TRBYVIhEuITaa357SEYDnv1lFbmGxz4lERMLP%0A458tB+Dsni3o0jw8V94OVSpEaoHzj0+jTaNEduwrZFxgl0gRETk8MzN28fXy7cREGberN6TGqRCp%0ABWKjo7j1NO83z7+mrGZPbqHPiUREwoNzjsc+9TZ7v6BvK9o2rutzosijQqSW+FXPFnROTWJvfjH/%0A/Ga133FERMLCV8u2MXvdbuJjorj51I5+x4lIKkRqiago484zvOlmL09dy5asPJ8TiYiEttJSx98C%0AY0OuOKEdzZITfE4UmVSI1CJD05vSr21DCopL+fsXK/2OIyIS0j6Yv5llmXtJSojh+sHH+B0nYqkQ%0AqUXMjLvO9HpF3pm9gVXb9vmcSEQkNBUWl/Lk5ysAuG7wMaQkxvqcKHKpEKll+rRpyGldmlHq4InJ%0Ay/2OIyISkt6atZ71u3JpkvTTJqJyZKgQqYV+f3o6ZjBpUSbzN+zxO46ISEjZV1C8//H1707tSGJc%0AjM+JIpsKkVooPTWJc3qnAfDopGU453xOJCISOsZ8u4adOYW0b1yXi/q28jtOxFMhUkvdOqwjcdFR%0ATFuzk29WbPc7johISNi2N58Xv1sDeL3HsdH6Y/JI07/hWiqtQSKjA889H/1kGSWl6hUREfn7FyvJ%0ALSyhd+v6nNE91e84tYIKkVrsxiEdSKkTy/Kte3nvx41+xxER8dXq7ft4a9YGAO45swtm5nOi2kGF%0ASC2WkhjLTUM7APDk5BXkFZb4nEhExD+Pfer1Dp/WpSn92jX0O06toUKklrtsYBta1q9DZnY+L/2Q%0A4XccERFfzFm3i88WbyXK4K4zOvsdp1ZRIVLLJcRG71/6/Z/frGbnvgKfE4mIHF3OOf7yibex3fl9%0AWtGxWZLPiWoXFSLC2ce2oHvLZPYVFPPsV6v8jiMiclRNWpTJnHW7SYiN4tZhnfyOU+uoEBGioox7%0Az+wCwGvT17Fmu5Z+F5HaoaC4hEcneb0h15x8DKkp2tjuaFMhIgAM6tCYoelNKC51+39TiohEuvHT%0A1u1fyv3ak9v7HadWUiEi+937iy5ERxmTl2xl2uqdfscRETmiducU8syX3lLudwzvRN14LeXuh0oV%0AImb2gJm5ckdm0HULtNlsZnlm9o2ZdSt3jwZmNt7MsgLHeDOrH3R9iJn918y2mFmOmc0zs5GHka21%0AmX0YeM8OM3vGzOIq8/1qu47NkrikX2sAHvp4CaVa5ExEItgzX60kO7+YzqlJnNdHS7n7pSo9IouB%0A5kFHj6BrdwK3ATcBfYFM4HMzCx6C/AbQCzgjcPQCxgddHwQsAM4FjgVeAl41s7MPFMjMooGPgbrA%0AicBFgfc/UYXvV6vdclpHkuJjWLw5mwlzN/kdR0TkiMjYkcP4aesA+MNZXm+w+KMqhUixcy4z6NgO%0AXm8IcAvwsHNugnNuETAKSAQuCbTpgld8XOWcm+acmwZcDfzSzNIBnHN/cc790Tk31Tm32jn3DPAp%0AMOIgmYYDXYFLnXNznXNfALcDV5tZchW+Y63VqF48N57iLXL2t8+WkVtY7HMiEZGa9+ikpRSXOoak%0AN+Gkjk38jlOrVaUQ6Rh49JJhZm+ZWdnonnZAKjC5rKFzrgCYgtfLATAQyHLOzQhqMx3ICmpTkRRg%0A10GuDwQWOec2B537DIgH+hze15Iyowe1Ja1BHbZmFzDm2zV+xxERqVHT1+zcv3jZvb/o4necWq+y%0AhcgM4HLgdLyejFRgqpk1CvwMsLXce7YGXUsFtlVw321Bbf6HmZ2H95hn3EFypZb/XOfcbqDwQPcN%0A3DvezJLLDkCr2OAtcnb3md7Kgi9MWUNmVr7PiUREakZJqePBD5cAcEn/1nTS4mW+q1Qh4pyb5Jx7%0Azzm3MPD446zApVHBzcq9zcqdq2gEZPk23kmzIcDLwNXOucWHine49w1yD15vTNmhnd8CzurRnD5t%0AGpBXVMJjn2o6r4hEhndmb2DplmySE2K4bVi633GEak7fdc7lAAuBjngDU+HnPRBN+am3IhNoVsGt%0AmlCuR8PMBgMfArc55149RJTM8p9rZg2A2PL3LecRvMc+ZUfaIT6n1jAz7v9lVwAmzN3Ej+t3+5xI%0ARKR6svOLePyz5QDcfFonGtbVxMpQUK1CxMzigS7AFiADryAYFnQ9DhgMTA2cmgakmFm/oDb98YqA%0AqUHnhuDNgrnbOTfmMKJMA7qbWfOgc8OBAmDOgd7knCtwzmWXHcDew/isWqNnq/qc18erzR78UNN5%0ARSS8PffVKnbmFNK+SV0uH9jG7zgSUNl1RB43s8Fm1i5QQLwLJAOvOOcc8DRwr5mNMLPueI9VcvGm%0A7OKcW4o3A2asmQ0wswHAWOAj59zywGcMwStCngHeM7PUwNEwKMcIMwt+XjAZWAKMN7PeZnYq8Dgw%0ANlBgSBXdeXo6deOimb9hDxPnaTqviISntTtyGBfYYfy+s7oQG631PENFZX8l0oA3geXABLzBoAOc%0Ac+sC1x/DK0aeB2YDLYHhzrk4rO4YAAAgAElEQVTgnoaReI9zJgeOBcBlQddH4035vQevp6XsmBDU%0AJgXY/3DPOVeCN14lH/gBeAeYCNxRye8n5TRNTuCmUzoC8OikZeQUaDqviISfhz9ZSlGJ4+ROTRia%0A3tTvOBLEvI4MAQjMnMnKysoiOVnLj5QpKC5h+FPfsm5nLjcOPYbfn97Z70giIoft+5U7uPTfM4iO%0AMj69+SQ6aqbMEZGdnU1KSgpASmWeRqhvSg4pPiaaPwTm2o/9LoP1O3N9TiQicniKSkp54ENv0uVl%0AA9qoCAlBKkTksAzr2owTOzSmsLiUhz5e4nccEZHD8srUtazato9GdeO4dVgnv+NIBVSIyGExM+4/%0Au+v+3XmnrNjudyQRkYPatjefp7/wdte984x0UurE+pxIKqJCRA5bp2ZJjB7UFoAHP1hMQXGJv4FE%0ARA7ir5OWs6+gmJ5pKZyv3XVDlgoRqZSbT+tI43rxrNmRw0vfr/U7johIheas28V7P3qLZT/wq25E%0AaXfdkKVCRColOSGWewL70Dz71Uq2ZOX5nEhE5H+VlDr+9IE3QPX8Pmn0bt3A50RyMCpEpNJG9G5J%0AnzYNyC0s4eGPl/odR0Tkf7w9awOLNmWTFB/DnWdouYFQp0JEKi0qyvjzr7sRZfDRgi1MXb3D70gi%0AIgDsyinksc+8hbdvGdaJJknxPieSQ1EhIlXSrUUKI/t7ezX86b+LKSop9TmRiAj8ddIy9uQW0Tk1%0AiVHaTyYsqBCRKrt9uLd75cpt+3jp+wy/44hILTdn3S7enr0BgIdHdCdG+8mEBf0qSZXVT4zbP3D1%0A6S9WsmmPBq6KiD+KS0q5b6I3QPWC49Po06bhId4hoUKFiFTLucel0bdtA/KKSngwMEpdRORoe3Xa%0AOpZuySalTix3aYBqWFEhItUSFWU89H89iAmsuPrl0q1+RxKRWmZbdj5Pfr4C8FZQbVRPA1TDiQoR%0Aqbb01CSuPLEdAH/6YDF5hVpxVUSOnoc+XuqtoNqqPhf1be13HKkkFSJSI353akdapCSwcXcez329%0A0u84IlJLfLtiOx/M30yUwUO/7k60VlANOypEpEbUjY/h/rO7ATDm2zWs3LrX50QiEunyi0q4b+Ii%0AAEYNakuPtBSfE0lVqBCRGnN6t2ac2rkpRSWOe99fSGmp8zuSiESwZ75cyfpduTRPSeD24el+x5Eq%0AUiEiNcbMePDX3UiMi2bW2t375/OLiNS05Zl7GfPtGgAe/FU36sXH+JxIqkqFiNSotAaJ3DasEwCP%0AfLKUbXvzfU4kIpGmtNTrdS0udQzv2ozh3VL9jiTVoEJEatzoQW3p0TKF7Pxi/vzhEr/jiEiEeWvW%0ABuas203duGge+FU3v+NINakQkRoXEx3FI+f02L8p3tfLtvkdSUQixLbsfB6d5O36ffvwdFrUr+Nz%0AIqkuFSJyRHRvmbJ/bZH7Ji4it7DY50QiEgnu/+9isvOL6dEyhVGD2vodR2qAChE5Ym4d1omW9euw%0AaU8ej3+2wu84IhLmPl20hU8XZxITZfz13GO1ZkiEUCEiR0xiXAwPj+gOwLipGfy4frfPiUQkXGXl%0AFvHH/3r7WV07uD1dWyT7nEhqigoROaKGpDflnN4tcQ7uencBBcVa/l1EKu8vnyxl+94C2jepy29P%0A6eh3HKlBKkTkiPvjL7vSuF4cK7ft4x9frfI7joiEmamrduxfl+jRc44lITba50RSk1SIyBHXoG4c%0AD/7Ke0Tz/DerWbol2+dEIhIu8gpLuHvCQgAuG9CGfu0a+pxIapoKETkqftEjldO7NaO41HHnuwso%0ALin1O5KIhIHHJy/fv4z7nWdoGfdIpEJEjgoz4//9ujvJCTEs3JTFi99n+B1JRELcrLW7eOkH7/8V%0AfzmnB0kJsT4nkiNBhYgcNU2TE7jvl10BePLzFazaph16RaRieYUl3PnuApyD8/ukMTS9qd+R5Aip%0AVCFiZg+YmSt3ZAZdt0CbzWaWZ2bfmFm3cvdoYGbjzSwrcIw3s/pB1xPM7GUzW2hmxWY28TCzra0g%0A26OV+X5y5J3fJ43BnZpQWFzK7f/RIxoRqdgTk5eTsSOH1KC/wEhkqkqPyGKgedDRI+jancBtwE1A%0AXyAT+NzMkoLavAH0As4IHL2A8UHXo4E84Bngi0pmu79ctocq+X45wsyMR8/tQVJCDPM37GHMd2v8%0AjiQiIWb22l38O/BI5pFzepBSR49kIllVCpFi51xm0LEdvN4Q4BbgYefcBOfcImAUkAhcEmjTBa/4%0AuMo5N805Nw24GvilmaUDOOdynHPXO+fG4hUylbG3XLZ9Vfh+coQ1T6nDn872Osqe/nwlyzP1iEZE%0APPlFJfw+8EjmvD5pDO2sRzKRriqFSMfAo5cMM3vLzNoHzrcDUoHJZQ2dcwXAFGBQ4NRAIMs5NyOo%0AzXQgK6hNddxlZjvNbJ6Z/cHM4g7W2MzizSy57ACSDtZeas65x7Xk1M5NKSwp5Y7/zKdIj2hEBPjb%0AZz89kvmjHsnUCpUtRGYAlwOn4/VkpAJTzaxR4GeAreXeszXoWipQ0Vas24LaVNXfgYuAocBzeL0z%0Azx/iPffgFUFlx8ZqZpDDZGb8JdDlunBTFv/8ZrXfkUTEZ9NW79w/S0aPZGqPShUizrlJzrn3nHML%0AnXNfAGcFLo0KblbubVbuXPnrFbWpNOfcU865Kc65Bc65F4HrgCsDRdKBPAKkBB1p1ckgldMsOYEH%0Af+U9onnmy5Us2pTlcyIR8cve/CLu+M98nIOL+7XWI5lapFrTd51zOcBCoCM/jeco37PRlJ96STKB%0AZhXcqgk/70mprumBf3Y4UAPnXIFzLrvsADRY4Sj7da8W+xc6u/XteeQXaS8akdrozx8uYdOePFo3%0ATOS+s7r4HUeOomoVImYWD3QBtgAZeIXGsKDrccBgYGrg1DQgxcz6BbXpj9cbUdampvQO/HNLDd9X%0AapCZ8ZcRPWhcL56V2/bxt8+W+x1JRI6yyYsz+c+cjZjBExf0pG58jN+R5Ciq7Doij5vZYDNrFygg%0A3gWSgVeccw54GrjXzEaYWXfgZSAXb8ouzrmlwKfAWDMbYGYDgLHAR8655UGf09XMegEN8QqXXoHX%0AZdf7mdkyM2sZeD3QzG4NtGtnZhcALwAfOOfWV/HfjRwljerF89h53izwf3+fwQ+rdvicSESOlh37%0ACrgnsJfMNSe3p29b7SVT21S2RyQNeBNYDkwACoEBzrl1geuP4RUjzwOzgZbAcOdc8COPkXiPcyYH%0AjgXAZeU+5xNgLnA2MCTw89yg64lAOlA2kqkAuBD4BlgC/BmvwLm4kt9PfHJK52Zc0r81AHf8Zz5Z%0AeUU+JxKRI805x70TFrIzp5D0ZkncNqyT35HEB+Z1ZAhAYApvVlZWFsnJyX7HqXVyCor5xTPfsW5n%0ALiN6t+SpC3sd+k0iErbenLmeeyYsJDbamHjjCXRrkeJ3JKmG7OxsUlJSAFIC4y4Pi/aakZBRNz6G%0AJy/oRZTB+3M38cH8zX5HEpEjZPX2ffz5wyUA/P70dBUhtZgKEQkpfdo04Kah3kSnP7y/kA27cn1O%0AJCI1rbC4lFvemkdeUQmDjmnEVSe2P/SbJGKpEJGQ87tTO3Jc6/rszS/m1rfnaWM8kQjz1BcrWLgp%0Ai5Q6sV4vaJT5HUl8pEJEQk5MdBR/v6g39eJjmL1uN//4WquuikSKaat38q8p3u/pv57bg9SUBJ8T%0Aid9UiEhIatUwkYf+rzsAf/9yBbPX7vI5kYhU157cQm57Zx7OwUV9W3FG9+Z+R5IQoEJEQtb/9W7J%0AiN4tKXVw81vzyM7XlF6RcOWc4/fvLmBLVj7tGtfVhnaynwoRCWl//nU3WjWsw6Y9edwzYSGabi4S%0Anl6ZupbPl2wlLjqKZy/urdVTZT8VIhLSkhJieeai3sREGR8v2MIbM7VQrki4WbQpi798sgyAe37R%0Ame4tNVVXfqJCREJe79YNuOuMzgA8+OESlmw+7HVyRMRn+wqK+e2bcyksKeW0Ls0YPait35EkxKgQ%0AkbBw5YntOKVzUwqLS7npjR/JKSj2O5KIHIb7Jy4iY0cOzVMS+Nt5x2Kmqbryv1SISFiIijIeP78n%0AqckJrNmRw30TF2m8iEiIe2f2BibM3USUwTMX96ZB3Ti/I0kIUiEiYaNh3Tieubg30VHG+3M38Z/Z%0AG/2OJCIHsHRLNn+cuAiAW0/rpF115YBUiEhY6deu4f4dOv/430UaLyISgvbmF3HD6z9SUFzKkPQm%0A3BjYtkGkIipEJOxcP/gYBndqQkFxKde/PoesPK0vIhIqnHPc9d4CMnbk0CIlgae0hLscggoRCTtR%0AUcbTF/aiZf06rNuZy+//M1/jRURCxMtT1/LJwkxio43nRh6ncSFySCpEJCw1qBvH8yOPIy46islL%0AtjLm2zV+RxKp9X5cv5uHP14KwB9+0YXjWjfwOZGEAxUiErZ6tqrP/Wd7y0T/9dNlTF+z0+dEIrXX%0A9r0F3PDajxSXOs7q0ZxRWi9EDpMKEQlrI/u35pzAfjQ3vTGXzKx8vyOJ1DpFJaXc+MaPZGbnc0yT%0Aujx6bg+tFyKHTYWIhDUz4+ERPeicmsSOfQVc99ocCopL/I4lUqv85ZOlzMzYRb34GMZcfjxJCbF+%0AR5IwokJEwl6duGjGXHY8KXVimbdhD/dPXKzBqyJHyftzNzLuh7UAPHlBT45pUs/fQBJ2VIhIRGjd%0AKJFnL+5NlMHbszfw2gxtjidypC3alMXd7y0E4HendGB4t1SfE0k4UiEiEePkTk24s2xzvA8WMzNj%0Al8+JRCLXzn0FXDt+DgXFpQxNb8Itp3XyO5KEKRUiElGuPbk9vzy2OcWljhten8PmPXl+RxKJOIXF%0ApVz/2o9s2pNH20aJPH1hby1aJlWmQkQiipnx2HnHBgavFnL1q7PJLdROvSI1xTnHnz5YxMy1u0iK%0Aj+HFUX1JSdTgVKk6FSIScRLjYhh7+fE0qhvH4s3Z3P7OfEpLNXhVpCa8MnUtb87c4O2oe0lvOjTV%0A4FSpHhUiEpFaNUzkX5f1ITbamLQok6e+WOF3JJGw993K7fz5oyUA3HNmF4amN/U5kUQCFSISsfq2%0AbchfRvQA4NmvVvHfeZt8TiQSvlZv38eNr/9IqYPz+qRx1Unt/I4kEUKFiES0849vxTUntwfg9+8u%0AYO763T4nEgk/O/cVcMW4WWTnF3Nc6/o8PKK7Vk6VGqNCRCLeXWd05tTOTSksLuXqV2ezYVeu35FE%0AwkZ+UQnXjJ/D+l25tGpYhzGXH098TLTfsSSCqBCRiBcdZfz94t50bZ7Mjn2FjB43k6zcIr9jiYS8%0A0lLHHf+Zz5x1u0lOiGHc6L40rhfvdyyJMJUqRMzsATNz5Y7MoOsWaLPZzPLM7Bsz61buHg3MbLyZ%0AZQWO8WZWP+h6gpm9bGYLzazYzCYeZraD3ldqt3rxMbw0ui/NUxJYvT2Ha8bP1p40IofwxOfL+WjB%0AFmKijH9d1ocOTZP8jiQRqCo9IouB5kFHj6BrdwK3ATcBfYFM4HMzC/6v9w2gF3BG4OgFjA+6Hg3k%0AAc8AX1Qi16HuK7VcakoCL43uS734GGZk7OKudxdoTxqRA3h71nr+8fVqAB45pweDjmnscyKJVFUp%0ARIqdc5lBx3bwekOAW4CHnXMTnHOLgFFAInBJoE0XvCLhKufcNOfcNOBq4Jdmlg7gnMtxzl3vnBuL%0AV8gc0uHcVwSgS/Nk/nnpccREGRPnbeaJyZrWK1Lel0u3cu/7iwD47SkdOP/4Vj4nkkhWlUKkY+DR%0AS4aZvWVm7QPn2wGpwOSyhs65AmAKMChwaiCQ5ZybEdRmOpAV1KYqqnRfM4s3s+SyA1C/Yy1wUscm%0A+6f1Pvf1KsZPW+trHpFQ8uP63dz4xo+UlDrO65PGbcO0h4wcWZUtRGYAlwOn4/U4pAJTzaxR4GeA%0AreXeszXoWiqwrYL7bgtqUxVVve89eMVK2bGxGhkkjFzQtxW3nNYRgPs/WMwnC7f4nEjEf6u37+PK%0Al2eRX1TKkPQmPHJOD03TlSOuUoWIc26Sc+4959xC59wXwFmBS6OCm5V7m5U7V9FD+fJtqqIq930E%0ASAk60qqZQcLIzad2ZGT/1jgHt7w1j6mrd/gdScQ327LzGfXSTHbnFtEzLYV/XHIcsdGaWClHXrX+%0AK3PO5QALgY78NJ6jfA9EU37qJckEmlVwqyb8vCelMqp0X+dcgXMuu+wA9lYjg4QZM+PPv+7OGd1S%0AKSwp5ZpX57BoU5bfsUSOuqzcIkaNm8XG3d5uui+N7kvd+Bi/Y0ktUa1CxMzigS7AFiADryAYFnQ9%0ADhgMTA2cmgakmFm/oDb98XojytpUxZG6r0S46Cjj6Yt60b9dQ/YVFDN63CwyduT4HUvkqMktLOaK%0Al2eydEs2TZLieeU3/WiktULkKKrsOiKPm9lgM2sX+IP+XSAZeMV58yCfBu41sxFm1h14GcjFm1qL%0Ac24p8Ckw1swGmNkAYCzwkXNuedDndDWzXkBDvAKjV+B12fV+ZrbMzFpW5r4iFUmIjWbsqOPp0jyZ%0AHfsKuPTFGWzak+d3LJEjrqC4hGvHz+HH9XtIqRPL+Cv70aZRXb9jSS1T2R6RNOBNYDkwASgEBjjn%0A1gWuP4ZXjDwPzAZaAsOdc8GPPEbiPc6ZHDgWAJeV+5xPgLnA2cCQwM9zg64nAulAbCXvK1Kh5IRY%0AXv1NP9o3rsumPXlc+uIMtu3N9zuWyBFTXFLKzW/O47uVO0iMi+blK/rSOTXZ71hSC5kWdPpJYApv%0AVlZWFsnJ+g1ZG23ek8f5/5rGpj15dE5N4q1rBlA/Mc7vWCI1qrTUced7C3h3zkbioqMYd0VfTuig%0ABcukerKzs0lJSQFICYy7PCwaEi0SpEX9Orx+VX+aJMWzLHMvo8bNYm++9qWRyFFa6vjDxEW8O2cj%0A0VHGs5f0VhEivlIhIlJO28Z1ef2q/jRIjGX+hj2MHjeLfQXFfscSqTbnHH/6YDFvzlxPlMGTF/Tk%0A9G7VWcJJpPpUiIhUoFOzJMZf2Z/khBjmrNvN6JdmqhiRsOac488fLWH89HWYwd/O68mve7X0O5aI%0AChGRA+neMoXXrupPUkIMs9ft5jfjZpGjYkTCkHOORyYtY9wPawH46znHcm4frd8ooUGFiMhBHJtW%0An9eu7E9SfAwz1+7iipdVjEh4cc7x8MdLGfPtGgAeHtGdC/pqEzsJHSpERA6hZ6v6jL8qUIxk7GL0%0AuJkawCphobTUGxPy4vcZAPz5190Y2b+Nz6lE/pcKEZHD0KtVfV69sh9J8THMWrubS1+cwZ7cQr9j%0AiRxQaanj3vcX8uo0b0zII+f04PKBbf2OJfIzKkREDlPv1g144+oB1E+MZf7GLC4aM50d+wr8jiXy%0AMyWljjvenc9bszYQFRiYenG/1n7HEqmQChGRSuiRlsLb1wykcT1vnZELX5hGZpZWYJXQUVBcwu/e%0AnMuEHzcF9lLqzXkamCohTIWISCWlpybxzrUDaJ6SwOrtOZz/wlTWaqM8CQE5BcVc9cpsPl64hdho%0A4x+X9OZXPVv4HUvkoFSIiFRB+yb1eOfagbRumMiGXXmc96+pLNqU5XcsqcV25xRyyYsz9u8d89Lo%0AvpzRvbnfsUQOSYWISBW1apjIu9cPpGvzZHbsK+SiMdOZumqH37GkFtqSlcf5L0xj/oY91E+M5Y2r%0AB3BSxyZ+xxI5LCpERKqhaVICb107gAHtG7KvoJjR42bxycItfseSWmR55l7OfX4qq7btIzU5gf9c%0AO5Berer7HUvksKkQEamm5IRYXr6iH2d0S6WwpJQb3/iRlwLrNogcSVNX7eC8f01lc1Y+7ZvU5d3r%0AB9KxWZLfsUQqRYWISA1IiI3mHyOPY2T/1jgHf/5oCQ98sJiSUud3NIlQ78/dyKhxM9mbX0zftg2Y%0AcP0g0hok+h1LpNJUiIjUkOgo46H/6849Z3YG4OWpa7nm1dlaEl5qlHOOZ79cya1vz6eoxHHWsc0Z%0Af2V/6ifG+R1NpEpUiIjUIDPj2sHH8PzI44iPieLLZdu4QGuNSA3JLyrh1rfn8cTnKwC49uT2PHtR%0AbxJio31OJlJ1KkREjoBf9GjOm9cMoFHdOBZvzubs577nx/W7/Y4lYWxbdj4XjpnOxHmbf+p9+0UX%0AoqLM72gi1aJCROQIOa51AybeeALpzZLYvreAi16YzjuzN/gdS8LQgo17+NVzP+yfnjv+yn5cOkCb%0A10lkUCEicgS1apjIhBsGcXq3ZhSWlHLnuwt48MPFFJeU+h1NwsT7czdy/r+mkZmdT4em9fjvjScw%0A6JjGfscSqTHmnEb1lzGzZCArKyuL5ORkv+NIBCktdTz71Sqe+sJ7tj+gfUOeubg3TZMSfE4moaqg%0AuIT/99ESXpu+HoCh6U145uLeJCXE+pxMpGLZ2dmkpKQApDjnsg/3fSpEgqgQkSPts8WZ3Pb2PHIK%0AS2iaFM+zF/emf/tGfseSELN5Tx43vP4j8zbsAeB3p3bk5lM7Eq3xIBLCVIjUABUicjSs2raPG16f%0Aw4qt+4iOMu48PZ1rTm6Pmf6QEfhu5XZufmseu3IKSU6I4e8X9WZo56Z+xxI5JBUiNUCFiBwtuYXF%0A3Pf+IibM3QTAaV2a8dh5x9KwrtaCqK2KSkp5YvIKXvh2Nc5B1+bJ/OvSPrRupEXKJDyoEKkBKkTk%0AaHLO8ebMDTzwwWIKS0pplhzPkxf04oQOGohY22zYlctv35y7/1HMJf1bc/8vu2p9EAkrKkRqgAoR%0A8cPizVn87s25rN6egxlcc3J7bh+WTlyMJrXVBh/M38wfJixkb0ExyQkx/PXcYzmzR3O/Y4lUmgqR%0AGqBCRPySV1jC//t4CW/M8GZI9GiZwpMX9NQGZhFsd04hf/zvIj5a4O3W3KdNA/5+US/tFyNhS4VI%0ADVAhIn77bHEmd723gD25RcTFRHHraZ24+qR2xESrdySSfLl0K3dPWMj2vQVERxk3Du3A707poF9n%0ACWsqRGqAChEJBVuz87n7vQV8vXw7AL1a1efx83vSoWk9n5NJdWXlFvHwJ0t4Z/ZGADo0rceTF/Tk%0A2LT6PicTqb6qFiKVKr/N7AEzc+WOzKDrFmiz2czyzOwbM+tW7h4NzGy8mWUFjvFmVr9cmx5mNiVw%0Aj01mdr8dYm5jBbmcmV1Xme8nEgqaJSfw0ui+/O28Y0mKj2Hehj384pnv+MfXqygs1oqs4cg5x0cL%0ANnPqk1N4Z/ZGzOCqE9vx0W9PVBEitV5MFd6zGDgt6HVJ0M93ArcBo4EVwH3A52aW7pzbG2jzBpAG%0AnBF4PQYYD5wN+3slPge+BvoCnYCXgRzgiUNkuwL4NOh11uF/LZHQYWacf3wrTuzYmLvfW8iUFdv5%0A22fLmTh3Ew+P6EG/dg39jiiHadOePO6fuIgvl20DoH2Tujx6zrH6NRQJqNSjGTN7APg/51yvCq4Z%0AsBl42jn318C5eGArcJdz7gUz6wIsAQY452YE2gwApgGdnXPLzex64BGgmXOuINDmbuC3QJo7QGAz%0Ac8AI59zEw/5CP7+HHs1IyHHOMXHeJh76aCk7cwoBuOD4NO45swsNtO5IyCooLmHcD2t55suV5BaW%0AEBtt3DCkAzcMPYb4GE3LlchzVB7NBHQMPHrJMLO3zKx94Hw7IBWYXNYwUEhMAQYFTg0EssqKkECb%0A6Xg9F8FtppQVIQGfAS2AtofI9pyZ7TCzWWZ2nZkd9PuZWbyZJZcdgKYoSMgxM0b0TuPL2wdzcb9W%0AALwzeyNDHv+GcT9kUKQN9ELO18u2ccbT3/HopGXkFpbQt20DJt18ErcO66QiRKScyj6amQFcjvfY%0ApRneo5epgXEgqYE2W8u9ZytQtl91KrCtgvtuC3p/KrC2gnuUXcs4QLY/Al8CecCpeI9xGgMPHeT7%0A3AP86SDXRUJG/cQ4HjnnWM7rk8Yf3l/Essy9PPjhEl6fsZ77zurCkHQtA+631dv38fDHS/kq8Bim%0Acb147j6zM+f0bkmU9okRqVClChHn3KSglwvNbBqwGhgFTC9rVu5tVu5cRY9WDtXGDnA+OFtwwTEv%0AMLb1fg5eiDwCPBn0OgnYeJD2Ir7r06YhH//uJN6atZ4nJq9g1bZ9jB43i8GdmnDnGel0a5Hid8Ra%0AZ1t2Pk9/uZK3Z22gpNQRE2X85sR2/PaUDtotV+QQqjJYdT/nXI6ZLQQ6AmVjM1KBLUHNmvJTj0Ym%0AXk9KeU3KtUktd73sr3rle1sOZjqQbGbNnHMVvi/w+Gf/IyBtOibhIjrKGNm/Db88tgXPfbWSl6eu%0AZcqK7UxZsZ1fHtuc24Z1on0TTfc90rLzi3hhymr+/X0G+UXeI7JTOzflnl900XRrkcNUrUIkMBi1%0AC/Ad3iOTTGAYMDdwPQ4YDNwVeMs0IMXM+jnnZgba9AdSgKlBbf5iZnHOucLAueF4A2HXViJebyAf%0A2FOlLycSBlLqxPKHs7oysn8bnvpiBR/M38xHC7YwaVEm5x2Xxo1DO2jTtCMgK7eIcVMzGPfDWrLy%0AigA4rnV97j6zi2bDiFRSZWfNPA58CKzH66W4D6/Q6OGcW2dmd+GNu7gCWAnc+//bu/fYKus7juPv%0Ab09v9gIUWkqBcr+qyFRE5yaghG3GwWaMussfapbodG6LyWZiliXTbC7LonEqm1l0Mv3HBTOZJrKx%0AOVEYzAleQiOCUK7l0pYWOC3tKW2/++M57Sp22paH/jjt55WQ0uc5PXz7y2nPh9/z/f0eYAnQvXzX%0AzNYSNZ7elX7a3wP73L1r+e5IYAfwT+BhotmWVcBD7v5I+jE3Ar909znpz5cTzaJsJuoRuZaoR2SV%0Au/+wH9+fVs1IRtt++CSPrNvBP7ZHPQqJLGP5JRXcvWQGs8epF/tsNTS38czGap7btI9kqh2INiW7%0A/8uzWXZhuWZVZVgblJ1VzewFYBFRE2gd0eWPn7r7B+nzRtT8eRdQQtTc+j13r+rxHKOBx4EV6UMv%0AA/e6+/Eej5kHrAQWAqDDVKEAAAiqSURBVI3AU0RBxNPnbweedXdLf/4Von6PGUQrgaqBp4GV7t7e%0Aj+9PQUSGhK37Gnn8tY94Y2dd97FlF5Zz56JpLJhcojfMfqqua+LZf+3lxa0HaTkdbZ00Z1wx9143%0Ag+svriChRlQRbfEeBwURGWqqak7w2/W7WFt1hK4f9YvGj+C2q6ewYv543Wb+U7g7m3Yf4w8b93Rv%0ARgbR+P1g6UyWzS3XShiRHhREYqAgIkPVrtomnt5QzUvv1pBKbxNfUpDDLQsquXlBpRore6hvSvHn%0Adw7ywtsHqK5r7j6+dM5YvvPFqXx++hjNKIn0QkEkBgoiMtQ1Nrfxpy0HeH7zPmqOt3Qfv3TSKG6+%0AvJKvzq9gxDBcbtrW3snGXXWs3nKQv39wlPbO6PdiQW6Cmy6byB1fmKJVSCKfQUEkBgoiMly0d3Ty%0A2oe1rN5ygNd31NGRfuPNzc5i8awybphXwdK5Y4f0Hhgdnc6/q4/xyvuHWFt1pHv1C8D8ylF844pK%0Als8fT1HeWS0uFBk2FERioCAiw1FtspWX3qlh9daD7Kpt6j6em53FopllLJ07lsWzyhg/6oKAVcbj%0AZOtpNuys57UPj7J+Rx0NzW3d58qK87hhXgW3XlHJ3Ar9/Iv0l4JIDBREZDhzd7YfTvLqtsO8uu0w%0A1fXNHzs/q7yIxbPKuHp6KZdNLmHkBef/bEmqvYP39h/nrT0NbN59jLf3NnRfdgEYVZDD9RdXsHx+%0ABVdOHaPVLyJnQUEkBgoiIhF3Z8fRJH+rOsobO2t578Bxerx/Ywazy4tZMKWESytLuGjCCKaXFZGT%0AGMh9NOOr+UBDC9tqTrCt5gTvHWjk3f3Hu5tzu0wvK+S6OWO5bk45C6aUBK1ZZChREImBgohI746f%0AamPDR/W8ubOOLfsa2XPGbAlAbiKLmeVFzB5XzNQxhUwaU8DkMYVMHl3AqIKcWFaauDvJVDtHT7Sy%0A99gp9tQ3UV3XTHV9MzuOJD/W59GltCiXK6eN4aqpo7lmZhlTSgvPug4R+SQFkRgoiIj0TV0yxdZ9%0ADfxnTyNVh06w/dDJ7p1Ge5ObyKK0KJfS4jxKi/Iozs+mIDdBfk6CgtwEOYksOj0KGu5wurOT5lQ7%0ATa3tNKXaOdnaTl0yxZETrd0bivUmJ2HMGTeCiyeMZN6EkSycOprpZYVabisyCBREYqAgIjIw7s7B%0AxhY+OHySnUeS7Gs4xf5jp9h7rJnaZOqzn6CfivOzqSwpYFpZIdNKC5lWVsSMsUXMKi8mN1uXWkRC%0AUBCJgYKISPxaT3dQ35SivqmN+mSK+qYUTal2Wto6OHW6g5a2Dto6OkmYYQZZZiSyjKK8bIrzsynK%0Ay6YoP5uyojzKR+RTPiKfC3K1I6zI+WagQUQL5EXknMrPSTCxpICJJboLsIh8kuYwRUREJBgFERER%0AEQlGQURERESCURARERGRYBREREREJBgFEREREQlGQURERESCURARERGRYBREREREJBgFEREREQlG%0AW7z34uTJPm+RLyIiIgz8vVM3vevBzCYAB0PXISIiksEmuntNXx+sINKDmRkwHkjG+LTFROFmYszP%0AO5xpTOOl8YyfxjR+GtN4navxLAYOeT/ChS7N9JAeuD6nuL6Isg0Ayf7cFln+P41pvDSe8dOYxk9j%0AGq9zOJ79fi41q4qIiEgwCiIiIiISjILIuZcCHkx/lHhoTOOl8YyfxjR+GtN4nTfjqWZVERERCUYz%0AIiIiIhKMgoiIiIgEoyAiIiIiwSiIiIiISDAKIoPMzF42s/1m1mpmh83seTMbH7quTGRmU8zsGTPb%0AY2YtZrbbzB40s9zQtWUyM/uJmW0ys1Nmdjx0PZnGzO5JvyZbzWyrmV0TuqZMZmaLzOwVMztkZm5m%0AXw9dUyYzswfM7G0zS5pZrZmtMbPZIWtSEBl8rwO3ALOBm4DpwItBK8pcc4hew3cBFwH3Ad8FHg5Z%0A1BCQC6wGfhe6kExjZrcCjwG/AC4FNgBrzWxS0MIyWyHwPnBv6EKGiMXASuAqYBnRDuvrzKwwVEFa%0AvhuYma0A1gB57n46dD2Zzsx+DNzt7tNC15LpzOx24DF3HxW6lkxhZm8B77j73T2ObQfWuPsD4Sob%0AGszMgRvdfU3oWoYKMysDaoHF7v5miBo0IxKQmY0Gvg1sUgiJzUigIXQRMvykLwleDqw749Q64OrB%0Ar0ikT0amPwb7vakgEoCZ/crMmoFjwCTga4FLGhLMbDrwfeCp0LXIsFQKJICjZxw/Cowb/HJEPl36%0AjvOPAhvdvSpUHQoiMTCzn6WbqD7tz4IeX/JrouvHXwI6gOesx60Qh7sBjCfpht+/Aqvd/ekwlZ+/%0ABjKmMmBnXu+2Xo6JnA+eBC4BvhmyiOyQ//gQ8iTwwmc8Zm/XX9y9HqgHdqavHx8gahzafK4KzDD9%0AGs90CHmdaPzuPHdlZbR+jakMSD3RfyzOnP0YyydnSUSCMrMngBXAInc/GLIWBZEY9AgWA9E1E5IX%0AUzkZrz/jaWYTiELIVuAOd+88l7VlqrN8jUofuHubmW0lWonwUo9Ty4C/hKlK5OPSs+9PADcCS9x9%0AT+CSFEQGk5ktBBYCG4FGYBrwELAbzYb0W3omZD2wH/gRUNZ1hcvdj4SrLLOll5qOJupfSpjZ59Kn%0Adrl7U7jKMsKjwPNmtoX/zdBNQn1LA2ZmRcCMHoempl+TDe6+P1BZmWwl8C2i3sSkmXXN4J1w95YQ%0ABWn57iAys3nAb4D5RGvjDxP1Nfzc3WtC1paJ0stLn+3tnLur52aAzGwVcFsvp6519/WDW03mMbN7%0AgPuBCqAKuC/UssihwMyWEM16numP7n774FaT+dJLoHtzh7uvGsxauiiIiIiISDBaNSMiIiLBKIiI%0AiIhIMAoiIiIiEoyCiIiIiASjICIiIiLBKIiIiIhIMAoiIiIiEoyCiIiIiASjICIiIiLBKIiIiIhI%0AMAoiIiIiEoyCiIiIiATzXyR6UONlQSa3AAAAAElFTkSuQmCC" alt="" />
Theta0 = 1.4072555867362913e-14
Theta1 = -0.6046983166379609
costs = [0.49746192893401031, 0.46273605725902511, 0.43457636303154484, 0.41174127378146347, 0.39322398105637657, 0.37820804982390627, 0.36603142151620471, 0.3561572235961119, 0.34815009862675572, 0.34165700918356962, 0.33639167228942018, 0.33212193708070803, 0.32865954918055734, 0.32585185048611698, 0.32357504841017987, 0.32172875781523191, 0.32023157499156085, 0.31901748853429884, 0.31803296887350535, 0.31723460813346771, 0.31658720626165587, 0.31606221904396564, 0.31563649957860979, 0.31529127771972282, 0.31501133249393021, 0.31478432100138809, 0.31460023421226618, 0.31445095566451636, 0.3143299036057311, 0.31423174080098198, 0.31415213921193808, 0.31408758917188512, 0.3140352446430773, 0.31399279773376704, 0.31395837694231021, 0.31393046464189178, 0.31390783016773566, 0.31388947555659158, 0.31387459154612474, 0.31386252189420782, 0.31385273444493683, 0.31384479766565831, 0.31383836162051826, 0.31383314254164574, 0.31382891031771304, 0.3138254783482301, 0.31382269531625501, 0.31382043851676622, 0.31381860844654841, 0.31381712441705512, 0.31381592099681721, 0.31381494512654245]
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAhkAAAFdCAYAAACuO39sAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz%0AAAAPYQAAD2EBqD+naQAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMS4xLCBo%0AdHRwOi8vbWF0cGxvdGxpYi5vcmcvAOZPmwAAIABJREFUeJzt3Xu0XWV97//3NxsSELM3ICJBDCBF%0A5HrAFMpFFIFUG9RWO1qwXuoBUUm9AB3VRn+A/pSD9SjEoh56ID89gFo8VSkXwYAColwsQYQIeA3I%0AJQmGy94BSQLJ9/fHmgsXK/uy5spee93erzHmSPacz3zmszLFfPLcVmQmkiRJk21auxsgSZJ6kyFD%0AkiS1hCFDkiS1hCFDkiS1hCFDkiS1hCFDkiS1hCFDkiS1hCFDkiS1hCFDkiS1hCFDkiS1hCFDkiS1%0AxGbtbsBUiYgAdgRWt7stkiR1oZnAw1niS8/6JmRQCRgPtrsRkiR1sZ2Ahxot3E8hYzXAAw88wODg%0AYLvbIklS1xgZGeFlL3sZlBwN6KeQAcDg4KAhQ5KkKeDET0mS1BKGDEmS1BKGDEmS1BKGDEmS1BKG%0ADEmS1BKGDEmS1BKGDEmS1BKGDEmS1BKGDEmS1BKGDEmS1BKGDEmS1BKGDEmS1BKGDEmS1BKGDEmS%0A1BKGDEmS1BKGDEmS1BKGDEmS1BJNhYyImB8RyyJiTUQsiYjDxyn77ojIUY4tytQZETMi4tyIWBUR%0AT0XEZRGxUzPtlyRJrVc6ZETEscBC4EzgAOBG4KqImD3ObSPArNojM9eUrHMh8BbgOODVwAuBKyJi%0AoOxnkCRJrReZWe6GiFuB2zPzpJpz9wCXZuaCUcq/G1iYmVs3W2dEDAG/B96ZmZcU13cEHgDmZeb3%0AGmj3IDA8PDzM4OBgg592bOs3JD9Z9hiPrF7D9jO34KBdt2VgWmxyvZIkdZqRkRGGhoYAhjJzpNH7%0ANivzkIiYDswBPlN3aTFw6Di3vjAi7gcGgDuA0zLzpyXqnANsXpwDIDMfjoilRZmNQkZEzABm1Jya%0AOe6HK+Hqpcv55OV3s3z4uc4YZg1twRlv2os37DNrsh4jSVJXKztcsh2VoLCy7vxKYIcx7rkXeDfw%0AZuBtwBrgxxGxe4k6dwDWZebjJZ67ABiuOR4co1wpVy9dzkkX3/68gAGwYngNJ118O1cvXT4Zj5Ek%0Aqes1u7qkfowlRjlXKZh5S2ZenJk/y8wbgb8Ffgl8sNk6GyxzFjBUc2zyJNH1G5JPXn73qA+snvvk%0A5XezfkO5IShJknpR2ZCxCljPxr0H27NxT8SoMnMD8F9AtSejkTpXANMjYptGn5uZazNzpHoAqxtp%0A33h+suyxjXownvdMYPnwGn6y7LFNfZQkSV2vVMjIzHXAEmBu3aW5wE2N1BERAewPLC9R5xLgmdoy%0AETEL2KfR506GR1aPHTCaKSdJUi8rNfGzcDZwUUTcBtwMvBeYDZwHEBEXAg9VV5pExBnALcCvgEHg%0AQ1RCxj80WmdmDkfEIuDzEfEo8BjwOeAu4NomPkNTtp+5xcSFSpSTJKmXlQ4ZmXlJRLwIOJ3KnhdL%0AqSwjvb8oMhvYUHPL1sD/pjIcMgz8FHhNZv6kRJ0ApwDPAt8EtgS+D7w7M9eX/QzNOmjXbZk1tMW4%0AQyYAjz+1bopaJElS5yq9T0a3mqx9Mr5758PM//pPxy0za2gLfvTRI903Q5LUE5rdJ8PvLilpm61m%0ATFjGyZ+SJBkySnPypyRJjTFklOTkT0mSGmPIKKk6+XMiTv6UJPU7Q0ZJA9OC047Zc8Jyn7rSnT8l%0ASf3NkNEEJ39KkjQxQ0YTnPwpSdLEDBlNcPKnJEkTM2Q0wcmfkiRNzJDRBCd/SpI0MUNGk5z8KUnS%0A+AwZTXLypyRJ4zNkNKnRSZ33rfpDi1siSVJnMmQ06aBdt2WHwYmHTP79v37nvAxJUl8yZDRpYFrw%0AtoNmT1jOeRmSpH5lyNgEu2y3VUPlnJchSepHhoxN4LwMSZLGZsjYBNVNuWKCcguv/SVXL10+JW2S%0AJKlTGDI2wcC04Iw37UUj0zo/ebkbc0mS+oshYxO9YZ9ZnHL07uOWSZwAKknqP4aMSeAEUEmSNmbI%0AmAROAJUkaWNNhYyImB8RyyJiTUQsiYjDG7zvuIjIiLi07nyOcfxTTZn7Rrn+mWbaP9ncmEuSpI2V%0ADhkRcSywEDgTOAC4EbgqIsbdmSoidgY+V5SvN6vuOJ7KVIZv1ZU7va7cp8u2vxXcmEuSpI0105Nx%0AKrAoMy/IzHsy82TgAeCksW6IiAHga8AZwG/rr2fmitoD+EvgusysL7u6ruyTTbS/JZyXIUnS85UK%0AGRExHZgDLK67tBg4dJxbTwd+n5mLGnjGS4BjgNHKfjQiHo2IOyLi40V7OkKj8zIaLSdJUrfbrGT5%0A7YABYGXd+ZXADqPdEBGHAScA+zf4jL8HVgPfrjv/BeB24HHgIOAsYFfgPWM8dwZQO1FiZoPPb0p1%0AY67lw+P3VDz+1LpWNkOSpI7R7OqS+tmLMco5ImImcDFwYmauarDu44GvZebz/rbOzHMy84bMvDMz%0ALwDeD5wQES8ao54FwHDN8WCDz2/KwLTgtGP2nLDcp650Uy5JUn8oGzJWAevZuNdiezbu3QDYDdgF%0AuDwino2IZ4F3AW8uft6ttnCxSmUP4IIG2nJL8eufjHH9LGCo5tipgTo3yTZbTbzCxMmfkqR+UWq4%0AJDPXRcQSYC7wnZpLc4H/HOWWe4F96859msrQxYepTBitdQKwJDN/1kBzDih+HfVLQTJzLbC2+nPE%0ARN8wsukandTp5E9JUj8oOycD4Gzgooi4DbgZeC8wGzgPICIuBB7KzAXFkMfS2psj4gmAzKw/Pwj8%0ADfCP9Q+MiEOAg4HrqAx9HAicA1yWmb9r4jO0hJtySZL0R6XnZGTmJcDJVFaM3AG8BpiXmfcXRWZT%0A2cOirOOozO34xijX1gLHAtcDdwP/L3A+8LYmntMybsolSdIfRWZ//GVX9JQMDw8PMzg42LLnfOHa%0AX3LOtb+asNw3TjyYQ3Yba86qJEmdY2RkhKGhIYChzBxp9D6/u2SSuSmXJEkVhoxJ5rwMSZIqDBmT%0AzHkZkiRVGDImmV+WJklShSGjBZyXIUmSIaMlnJchSZIhoyWclyFJkiGjJZyXIUmSIaNlnJchSep3%0AhowWcV6GJKnfGTJaxHkZkqR+Z8hoEedlSJL6nSGjhZyXIUnqZ4aMFnJehiSpnxkyWsh5GZKkfmbI%0AaCHnZUiS+pkho8WclyFJ6leGjBZzXoYkqV8ZMlrMeRmSpH5lyGgx52VIkvqVIWMKOC9DktSPDBlT%0AwHkZkqR+ZMiYAs7LkCT1o6ZCRkTMj4hlEbEmIpZExOEN3ndcRGREXFp3/qvF+drjlroyMyLi3IhY%0AFRFPRcRlEbFTM+2fas7LkCT1o9IhIyKOBRYCZwIHADcCV0XEuH+LRsTOwOeK8qO5GphVc8yru74Q%0AeAtwHPBq4IXAFRExUPYztIPzMiRJ/aaZnoxTgUWZeUFm3pOZJwMPACeNdUMRBL4GnAH8doxiazNz%0ARc3xWM39Q8AJwD9m5rWZ+VPgHcC+wNFNfIYp57wMSVK/KRUyImI6MAdYXHdpMXDoOLeeDvw+MxeN%0AU+aIiHgkIn4ZEedHxPY11+YAm9c+NzMfBpaO9dxieGWwegAzx3l2yzkvQ5LUb8r2ZGwHDAAr686v%0ABHYY7YaIOIxKL8SJ49R7FfB24EjgH4EDgR9ERPVv5R2AdZn5eKPPBRYAwzXHg+M8v+WclyFJ6jfN%0Ari6p/6d2jHKOiJgJXAycmJmrxqws85LMvDIzl2bm5cBfAK8AjpmgHaM+t3AWMFRztH2SaKPzMq65%0Ae0WLWyJJUuuVDRmrgPVs3HuwPRv3bgDsBuwCXB4Rz0bEs8C7gDcXP+822kMyczlwP7B7cWoFMD0i%0AtmnwuWTm2swcqR7A6gk/XYs1Oi/jP+942CETSVLXKxUyMnMdsASYW3dpLnDTKLfcS2Vy5v41x2XA%0AdcXvHxjtORHxIuBlwPLi1BLgmdrnRsQsYJ8xntuRDtp1W7bdavMJyz361DqHTCRJXW+zJu45G7go%0AIm4DbgbeC8wGzgOIiAuBhzJzQWauoTI58zkR8QRAZi4tfn4h8AngW1RCxS7A/6DSa/KdouxwRCwC%0APh8RjwKPUVkOexdwbROfoS0GpgVv2f+lLPrxfROWdSmrJKnblQ4ZmXlJ0dNwOpX9LJYC8zLz/qLI%0AbGBDiSrXU+nteBewNZWgcR1wbGbWDnGcAjwLfBPYEvg+8O7MXF/2M7TT0Xvt0FDIcCmrJKnbRWZ/%0AjP0Xy1iHh4eHGRwcbFs71m9IDvvM91kxsnbccrOGtuBHHz2SgWkxRS2TJGl0IyMjDA0NAQwV8xwb%0A4neXTDGXskqS+oUhow1cyipJ6geGjDZwKaskqR8YMtrApaySpH5gyGiD6lLWRriUVZLUrQwZbXL0%0AXmN95crzuZRVktStDBlt4reySpJ6nSGjTVzKKknqdYaMNnIpqySplxky2silrJKkXmbIaCOXskqS%0Aepkho43KLGV1yESS1G0MGW3W6FJWh0wkSd3GkNFmDplIknqVIaPN3P1TktSrDBkdwN0/JUm9yJDR%0AAdz9U5LUiwwZHcDdPyVJvciQ0SHc/VOS1GsMGR3C3T8lSb3GkNEhXMoqSeo1howO4e6fkqReY8jo%0AIO7+KUnqJU2FjIiYHxHLImJNRCyJiMMbvO+4iMiIuLTm3OYR8S8RcVdEPBURD0fEhRGxY9299xX3%0A1h6faab9ncohE0lSLykdMiLiWGAhcCZwAHAjcFVEjLsGMyJ2Bj5XlK/1AuBVwKeKX98KvAK4bJRq%0ATgdm1RyfLtv+TuaQiSSplzTTk3EqsCgzL8jMezLzZOAB4KSxboiIAeBrwBnAb2uvZeZwZs7NzG9m%0A5i8y8xbgg8CcUYLL6sxcUXM82UT7O5pDJpKkXlEqZETEdGAOsLju0mLg0HFuPR34fWYuavBRQ0AC%0AT9Sd/2hEPBoRd0TEx4v2jNXWGRExWD2AmQ0+u60cMpEk9YqyPRnbAQPAyrrzK4FR/wkeEYcBJwAn%0ANvKAiNgC+Azw9cwcqbn0BeA44HXAF4GTgS+PU9UCYLjmeLCR57ebQyaSpF7R7OqS+n76GOUcETET%0AuBg4MTNXTVRpRGwO/HvRrvnPe2DmOZl5Q2bemZkXAO8HToiIF41R3VlUekSqx04TPb9TOGQiSeoF%0Am5UsvwpYz8a9Ftuzce8GwG7ALsDlEVE9Nw0gIp4F9sjM3xQ/bw58E9gVOLKuF2M0txS//gnwaP3F%0AzFwLrK3+XPP8jlcdMnnsqWfGLVcdMjlkt7FyliRJ7VOqJyMz1wFLgLl1l+YCN41yy73AvsD+Ncdl%0AwHXF7x+A5wWM3YGjM3Oj0DCKA4pfl5f5DN3AIRNJUi9oZrjkbOA9EXF8ROwZEecAs4HzAIo9Ls4C%0AyMw1mbm09qAymXN18fO6iNgM+A/gT4G3AwMRsUNxTC/qPCQiTomI/SNi14j4W+DfgMsy83eb+ofQ%0AiRwykSR1u7LDJWTmJcU8iOqeFUuBeZl5f1FkNrChRJU7AW8ufn9H3bXXAddTGfY4lsoS2BnA/cD5%0AwGfLtr9bOGQiSep2kdkf/woulrEODw8PMzg42O7mNORTl/+cRT++b8Jyxx+2C6e/ae/WN0iS1JdG%0ARkYYGhoCGGpgzuRz/O6SDtbokMk3b3vQIRNJUscxZHSwRjfmenLts3zxB7+eghZJktQ4Q0YHK7PK%0A5Cs3LbM3Q5LUUQwZHa7RIZMn/vCM24xLkjqKIaPDHbTrtmy95cRDJuCeGZKkzmLI6HAD04L/ftgu%0ADZV1zwxJUicxZHSBDxy5O1vNGJiwnN/MKknqJIaMLjAwLTjuT1/WUFmHTCRJncKQ0SXcZlyS1G0M%0AGV2i0T0zHDKRJHUKQ0aX8JtZJUndxpDRRdxmXJLUTQwZXcRtxiVJ3cSQ0UXcZlyS1E0MGV3GbcYl%0ASd3CkNFl3GZcktQtDBldpsw2404AlSS1kyGjCzW6zbgTQCVJ7WTI6EJlthl3AqgkqV0MGV3KCaCS%0ApE5nyOhSTgCVJHU6Q0aXcgKoJKnTGTK6mBNAJUmdrKmQERHzI2JZRKyJiCURcXiD9x0XERkRl9ad%0Aj4j4REQ8HBFPR8T1EbF3XZltIuKiiBgujosiYutm2t8rykwA/bcf/sbeDEnSlCodMiLiWGAhcCZw%0AAHAjcFVEzJ7gvp2BzxXl630EOBX4AHAgsAK4JiJm1pT5OrA/8Ibi2B+4qGz7e02jE0D/sG69vRmS%0ApCnVTE/GqcCizLwgM+/JzJOBB4CTxrohIgaArwFnAL+tuxbAycCZmfntzFwK/D3wAuDvijJ7UgkW%0A78nMmzPzZuBE4I0RsUcTn6FnlJkA6nJWSdJUKhUyImI6MAdYXHdpMXDoOLeeDvw+MxeNcm1XYIfa%0AOjNzLXBDTZ2HAMOZeWtNmVuA4bGeGxEzImKwegAzRyvX7cpMAHU5qyRpKpXtydgOGABW1p1fSSUo%0AbCQiDgNOoNLzMJrqfePVuQPwyCj3PjLWc4EFVEJI9XhwjHJd7wNH7s4Lpk88ARTgez9f3uLWSJJU%0A0ezqkvo+9xjlHMWciouBEzNz1SbWOVo//6jPLZwFDNUcO03w/K41MC1432te3lDZC2++n+/eadCQ%0AJLVe2ZCxCljPxr0H27NxTwTAbsAuwOUR8WxEPAu8C3hz8fNuVCZ5MkGdK4CXjFL/i8d4Lpm5NjNH%0AqgewetxP1uUaXc66IWH+12/n6qUGDUlSa5UKGZm5DlgCzK27NBe4aZRb7gX2pbISpHpcBlxX/P4B%0AYBmVEPFcncXcj9fW1HkzMBQRB9WU+TMqPRSjPbfvlFnOCvDP377LSaCSpJZqZrjkbOA9EXF8ROwZ%0AEecAs4HzACLiwog4CyAz12Tm0toDeAJYXfy8LjOTypLYj0XEWyJiH+CrwB+oLFslM+8BrgbOj4iD%0AI+Jg4Hzgisz8xab8AfSSRpezQmUSqEtaJUmtVDpkZOYlVJacng7cAbwGmJeZ9xdFZgOzSlb7WSpB%0A48vAbcBLgT/PzNohjrcDd1FZhbIYuBN4Z9n297KDdt2WWUNbNFzeDbokSa0UlY6E3lcsYx0eHh5m%0AcHCw3c1pmauXLuf9F9/ecPlTjn4FHz569xa2SJLU7UZGRhgaGgIYKuY5NsTvLukxb9hnFl/+uwOI%0ABsvbmyFJahVDRg+at9+OfPioxnon3G5cktQqhowe9cGjGt+gy94MSVIrGDJ6VJkNuuzNkCS1giGj%0Ah5XZbtzeDEnSZDNk9DB7MyRJ7WTI6HH2ZkiS2sWQ0ePszZAktYshow/YmyFJagdDRh+wN0OS1A6G%0AjD5hb4YkaaoZMvqEvRmSpKlmyOgj9mZIkqaSIaOP2JshSZpKhow+Y2+GJGmqGDL6jL0ZkqSpYsjo%0AQ/ZmSJKmgiGjD9mbIUmaCoaMPlWmN+O8G35tb4YkqTRDRp8q05vx9DMb+PC//7TFLZIk9RpDRh8r%0A05txxZ3L+e6dy1vcIklSLzFk9LEyvRkAH/nWnQ6bSJIa1lTIiIj5EbEsItZExJKIOHycsm+NiNsi%0A4omIeCoi7oiId9aVyTGOf6opc98o1z/TTPv1R2V6M55c+6yTQCVJDSsdMiLiWGAhcCZwAHAjcFVE%0AzB7jlseKsocA+wFfAb4SEa+vKTOr7jgeSOBbdXWdXlfu02Xbr+cr25vhJFBJUqOa6ck4FViUmRdk%0A5j2ZeTLwAHDSaIUz8/rM/E5R9jeZ+QXgTuDVNWVW1B7AXwLXZeZv66pbXVf2ySbarzofOHJ3tprR%0AWG+Gk0AlSY0qFTIiYjowB1hcd2kxcGgD90dEHAXsAfxwjDIvAY4BFo1y+aMR8Wgx5PLxoj3aRAPT%0Agv/51/s1XN5JoJKkRpTtydgOGABW1p1fCeww1k0RMRQRTwLrgCuBD2bmNWMU/3tgNfDtuvNfAI4D%0AXgd8ETgZ+PI4z5wREYPVA5g55qcS8/bbkTftN+Yr3IiTQCVJE2l2dUn93y4xyrlaq4H9gQOBjwNn%0AR8QRY5Q9HvhaZq553gMzz8nMGzLzzsy8AHg/cEJEvGiMehYAwzXHg+O0T8DC417lJFBJ0qQpGzJW%0AAevZuNdiezbu3XhOZm7IzF9n5h2Z+XngP6iEgOcpVqnsAVzQQFtuKX79kzGunwUM1Rw7NVBnX3MS%0AqCRpMpUKGZm5DlgCzK27NBe4qURVAcwY5fwJwJLM/FkDdRxQ/Drq5IDMXJuZI9WDSm+KJuAkUEnS%0AZGlmuORs4D0RcXxE7BkR5wCzgfMAIuLCiDirWjgiFkTE3Ih4eUS8MiJOBd4FXFxbaTFv4m8YpRcj%0AIg6JiFMiYv+I2DUi/hb4N+CyzPxdE59BY3ASqCRpsmxW9obMvKSYB1Hds2IpMC8z7y+KzAY21Nyy%0AFZUJmjsBTwP3Au/IzEvqqj6OSg/HN0Z57FrgWOAMKj0g9wPnA58t235NbN5+O/Kmpcu5/M4VDZX/%0Ap//4Ga/fZwcGpkWLWyZJ6iaR2R9j6kVPyfDw8DCDg4Ptbk7HW78h2fcT3+MP69Y3VP6YfXfgS2+f%0A0+JWSZLaYWRkhKGhIYChYgpCQ/zuEo2q7CTQK+9awZlX3t3CFkmSuo0hQ2MqMwkU4Pwblzk/Q5L0%0AHEOGxlR2EihU5me4rFWSBIYMTaDsTqBPrVvvslZJEmDIUAMWHveqUsMmLmuVJIEhQw1w2ESS1AxD%0Ahhoyb78dOfHwXRou/9S69XzoG7e3rkGSpI5nyFDDPn7M3hyzb+PzM1zWKkn9zZChUv71beXmZ7is%0AVZL6lyFDpTg/Q5LUKEOGSmtmWavzMySp/xgy1JSyy1qvvGsFn7ri5y1skSSp0xgy1JRmhk0W/eg+%0Ag4Yk9RFDhppWdlkrVIKGK04kqT8YMrRJyi5rBVecSFK/MGRok5Vd1gquOJGkfmDI0CZrZn7GU+vW%0A8/YLbjFoSFIPM2RoUjQzP+OW3z7Gfp/8Ht+98+HWNEqS1FaGDE2ajx+zNye8epdS9zy1dj3zv/5T%0AzrzSVSeS1GsMGZpUp72xfNAAOP9Gl7dKUq8xZGjSnfbG8itOwH00JKnXGDLUEs2sOAGDhiT1EkOG%0AWqKZFSdVBg1J6g1NhYyImB8RyyJiTUQsiYjDxyn71oi4LSKeiIinIuKOiHhnXZmvRkTWHbfUlZkR%0AEedGxKqinssiYqdm2q+pMW+/HXnfa3Zt6l6DhiR1v9IhIyKOBRYCZwIHADcCV0XE7DFueawoewiw%0AH/AV4CsR8fq6clcDs2qOeXXXFwJvAY4DXg28ELgiIsr3yWvKLJi3F1/+u1ex1XSHTiSp30Rmuc2Q%0AIuJW4PbMPKnm3D3ApZm5oME6bgeuzMzTip+/CmydmX81Rvkh4PfAOzPzkuLcjsADwLzM/F4DzxwE%0AhoeHhxkcHGykmZpE6zckH/rG7Vx514rS957w6l047Y17t6BVkqRGjIyMMDQ0BDCUmSON3leqJyMi%0ApgNzgMV1lxYDhzZwf0TEUcAewA/rLh8REY9ExC8j4vyI2L7m2hxg89rnZubDwNKxnlsMrwxWD2Dm%0ARO1T6wxMC7709jlNLW+1R0OSutNmJctvBwwAK+vOrwTGXLNY9EQ8BMwA1gPzM/OamiJXAf8XuB/Y%0AFfgU8IOImJOZa4u612Xm4yWeuwA4o5EPpalT7ZFY9KP7St1XLW+PhiR1j7Iho6p+jCVGOVdrNbA/%0AlXkURwFnR8RvM/N6gOoQSGFpRNxGJXAcA3x7nHrHe+5ZwNk1P88EHhynLk0Rg4Yk9YeyIWMVlZ6I%0A+t6D7dm4d+M5mbkB+HXx4x0RsSeVnobrxyi/PCLuB3YvTq0ApkfENnW9GdsDN41Rx1pgbfXniBir%0AeWqDTQkay594mnP/bg4D03ynktTJSs3JyMx1wBJgbt2luYzxl/0YgsrQyegXI14EvAxYXpxaAjxT%0A+9yImAXsU/K56iDNbkH+3aUr2fv0q/1iNUnqcM3sk3E28J6IOD4i9oyIc4DZwHkAEXFhRJxVLRwR%0ACyJibkS8PCJeGRGnAu8CLi6uvzAiPhcRh0TELhFxBHA5lV6T7wBk5jCwCPh8RBwVEQcU998FXNvk%0AZ1cHaDZorHl2g1+sJkkdrvScjMy8pOhpOJ3KfhZLqSwjvb8oMhvYUHPLVsCXgZ2Ap4F7gXfUzMNY%0AD+xLJXhsTaX34jrg2MxcXVPPKcCzwDeBLYHvA+/OzPVlP4M6S7NDJ1D5YrUN6TwNSepEpffJ6Fbu%0Ak9H5PnXFz5sKGgDz9nmJ8zQkqUWmZJ8MqZWaHToB52lIUicyZKijbErQcJ6GJHUWQ4Y6zqYEDajM%0A05h/8W2s39AfQ4GS1KkMGepIp71xb048vLlvcAWHTySpExgy1LE+fkzlG1xnDDQ3mbM6fPIPX7NX%0AQ5LawdUl6njrNyQf+vrtXLm0/De4Vm2x2TTO/tv/xrz9dpzElklSf3B1iXrWwLTgS+9o7htcq+zV%0AkKSpZ8hQ19jUeRoAV961klf+P1ex8JpfGDYkqcUcLlHX+e6dyznlkp+ydv2m/W/XIRRJakyzwyWG%0ADHWlyZinUXXMvi/hX9/mbqGSNBZDxgQMGb3pzCvv5vwbl21yPZtPg6P32oF3HLwzB7/8RQYOSaph%0AyJiAIaN3TdbwSdWMzYKTXrsbHzzqFYYNScKQMSFDRm9bvyH58Dd+yhV3LZ+0OjefFvzD6wwbkmTI%0AmIAhoz9Mdq8GGDYkyZAxAUNG/2hFrwYYNiT1L0PGBAwZ/ee7dy7n1G/ewZpnN0xqvYYNSf3GkDEB%0AQ0Z/Wr8hOff7v+KLP/gVz07y/9QHAubu9RLeecgurkiR1NMMGRMwZPS3Vg2hVLkiRVIvM2RMwJAh%0AqAyhfORbd/Lk2mdbUr+9G5J6kSFjAoYMVa3fkNzym0e5+Nb7uPbuR3imRd9hYu+GpF5hyJiAIUOj%0Aqc7Z+NJ1v25Z2LB3Q1K3M2RMwJCh8UxF2IDK9uVH7WngkNRdDBkTMGSoEVMVNgA2Czhg5204aNdt%0AOXS37QwdkjrWlIaMiJgP/BMwC/g5cHJm3jhG2bcCHwP+BNgc+BXw+cy8qLi+OfBpYB7wcmAYuBb4%0A58x8uKae+4Cd66r/l8z85wYV9C2kAAANZ0lEQVTbbMhQw6YybFTZyyGpU01ZyIiIY4GLgPnAj4H3%0AAe8B9srM341S/ghgG+BeYB3wRuDzwDGZ+b2IGAL+Azgf+FlRdiGwWWb+aU099wGLinJVT2bmkw22%0A25Ch0toRNqAyafSIV7yYLadvxku32dKeDkltNZUh41bg9sw8qebcPcClmbmgwTpuB67MzNPGuH4g%0A8BNg52pwKULGwsxcWKrBf6zTkKGmVcPGeTf8ZtJ3EG2UwyuS2mVKQkZETAf+APxNZn6n5vwXgP0z%0A87UT3B/AkcBlwF9l5jVjlDsaWAxsXf0wRciYAUwHHgD+L/A/M3PdGHXMKMpXzQQeNGRoU1SXv154%0Ay31ce89K1rcnbwCV0LH/7K3ZaZsX2NshqaWmKmTsCDwEHJaZN9Wc/xjw95m5xxj3DRX3zQDWA/Mz%0A8/8bo+wWwI+AezPzHTXnTwFuBx4HDgLOAv4zM98zRj2fAM6oP2/I0GTphN6NevZ2SGqFqQ4Zh2bm%0AzTXnPw68MzNfOcZ906hM6nwhcBRwGpWejOvrym1OpYdiNnDEeB8kIv6aylyO7TLz0VGu25OhKdFJ%0AvRv1qr0dL916SyLCHg9JTemK4ZKa8hcAL8vM19ec2xz4JpUwcuRowaGujpcCDwIHZ+atDTzTORlq%0AuU7s3RiN4UNSGVM98XNJZs6vOXc3laGLRid+LgJ2y8wjip+rAWN34HWZ+fsG6ngjcDk1k0MnKG/I%0A0JSp7d34wb2P8Mz67tiPpjZ8AAYQSUB7lrC+H7gZeC9wIrB3Zt4fERcCD1UDR0QsAG4DfkNl0uY8%0A4F+AkzLzgojYDPgW8Coqy1tX1jzuscxcFxGHAAcD11HZR+NA4Bzgtsz8ywbbbchQW3Rr4Kg3fSD4%0AbzsNsWMRQKoMIlLva8dmXB+hshnXUuCUzPxhce164L7MfHfx86eBY4GdgKep7Jfxhcy8pLi+C7Bs%0AjEe9LjOvj4hXAV8GXkllnsX9wL8Dn83MPzTYZkOG2q4aOH78m9/zX8se444Hh7s2dIymvieklmFE%0A6l5uKz4BQ4Y6UW0vxw2//D1rnunceRyTabwwUmUokTqHIWMChgx1uvUbkp8se4wVw0+z6sm13Hb/%0A4109vDKZavcEmbX1Fmy95XSeeHodDz/+9Jj3GFKkyWPImIAhQ92o14dXpkojPSdlGGDUbwwZEzBk%0AqBfUho6HHn+ah5942uDRZtMH4I37zeIlQ1uO27MyFSJi3J4ew5GaZciYgCFDvcreDjVjsnt3RjNR%0A6Jlq/dKeVoRJQ8YEDBnqF/W9HYA9HlKf2voFm/OZt+7LG/aZtUn1GDImYMhQvzN8SP3rvHe8apOC%0AhiFjAoYMaXSjhY+q5cNr+NmDw6zt4C3SJU1s1tAW/OijRzY9dNJsyNisqadJ6hkD04LDdt+Ow3bf%0AbtTr44UQe0Kk7rB8eA0/WfYYh+z2oil9riFD0rg2JYRUGUak9ntk9Zopf6YhQ9ImmSiEVDUSRqoM%0AJdLk237mFlP+TEOGpCnRaBipGi2UNLrkz5AiPd+soS04aNdtp/y5hgxJHalsKKlXpuekDAOMutEZ%0Ab9qrLZuvGTIk9aRNDSnjqQaYm3+7ig0JQ1tu3vGbOxmO+tM2L9icsyZhn4xmGTIkqaRWBphWalXv%0Azlj6ZYfNTmtPJ20fb8iQpD7RreFI3WtauxsgSZJ6kyFDkiS1hCFDkiS1hCFDkiS1hCFDkiS1hCFD%0AkiS1hCFDkiS1hCFDkiS1RFMhIyLmR8SyiFgTEUsi4vBxyr41Im6LiCci4qmIuCMi3llXJiLiExHx%0AcEQ8HRHXR8TedWW2iYiLImK4OC6KiK2bab8kSWq90iEjIo4FFgJnAgcANwJXRcTsMW55rCh7CLAf%0A8BXgKxHx+poyHwFOBT4AHAisAK6JiJk1Zb4O7A+8oTj2By4q235JkjQ1IrPcl+VExK3A7Zl5Us25%0Ae4BLM3NBg3XcDlyZmadFRAAPAwsz81+K6zOAlcBHM/PfImJP4G7g4My8tShzMHAz8MrM/EUDzxwE%0AhoeHhxkcHCzzkSVJ6msjIyMMDQ0BDGXmSKP3lerJiIjpwBxgcd2lxcChDdwfEXEUsAfww+L0rsAO%0AtXVm5lrghpo6DwGGqwGjKHMLMDzWcyNiRkQMVg9g5mjlJElSa5T9grTtgAEqvQy1VlIJCqOKiCHg%0AIWAGsB6Yn5nXFJer941W5841ZR4ZpepHxnnuAuCMsdokSZJaq9nVJfVjLDHKuVqrqcyhOBD4OHB2%0ARBxRss7R6h/vuWcBQzXHTuO0T5IkTbKyPRmrqPRE1PcebM/GPRHPycwNwK+LH+8o5lgsAK6nMsmT%0Aos7lY9S5AnjJKFW/eKznFkMua6s/V6Z+SJKkqVKqJyMz1wFLgLl1l+YCN5WoKqgMnQAsoxIinquz%0AmPvx2po6bwaGIuKgmjJ/RqWHosxzJUnSFCnbkwFwNnBRRNxG5S//9wKzgfMAIuJC4KHqSpOIWADc%0ABvwGmA7MA94FnASQmRkRC4GPRcSvgF8BHwP+QGXZKpl5T0RcDZwfEe8r2vG/gSsaWVkiSZKmXumQ%0AkZmXRMSLgNOBWcBSYF5m3l8UmQ1sqLllK+DLVOZEPA3cC7wjMy+pKfNZYMui3DbArcCfZ+bqmjJv%0AB/6VP65CuYzKvhqSJKkDld4no1u5T4YkSc1pdp+MZoZLutrISMN/NpIkieb/7uynnoyXAg+2ux2S%0AJHWxnTLzoUYL91PICGBHKnt2TJaZVILLTpNcrzad76Zz+W46l++mc3XCu5kJPJwlgkPfDJcUfygN%0Ap69G1Oy9sbrMGJVaz3fTuXw3nct307k65N2Ufm6zO35KkiSNy5AhSZJawpCxadYCn6Rm+3J1DN9N%0A5/LddC7fTefqynfTNxM/JUnS1LInQ5IktYQhQ5IktYQhQ5IktYQhQ5IktYQhYxNExPyIWBYRayJi%0ASUQc3u429bqIeE1EXB4RD0dERsRf1V2PiPhEcf3piLg+IvauK7NNRFwUEcPFcVFEbD21n6S3RMSC%0AiPiviFgdEY9ExKURsUddmRkRcW5ErIqIpyLisojYqa7M7OL9PlWU+9eImD61n6a3RMRJEXFnRIwU%0Ax80R8Rc1130vHaD4bygjYmHNua5/N4aMJkXEscBC4EzgAOBG4KqImN3WhvW+rYCfAR8Y4/pHgFOL%0A6wcCK4BrImJmTZmvA/sDbyiO/YGLWtXgPvFa4EvAwcBcKrsJL46IrWrKLATeAhwHvBp4IXBFRAwA%0AFL9eSeUdv7oo99fA56foM/SqB4F/Bv60OH4A/GdN+Pa9tFlEHAi8F7iz7lL3v5vM9GjiAG4F/lfd%0AuXuAs9rdtn45gAT+qubnAJYDH605NwN4Anhf8fOexX1/VlPm4OLcHu3+TL1yAC8u/kxfU/w8BKwD%0Ajq0psyOwHnh98fNfFD/vWFPmOGANMNjuz9RLB/AYcILvpf0HleDwS+Bo4HpgYXG+J96NPRlNKLqi%0A5gCL6y4tBg6d+hapsCuwAzXvJTPXAjfwx/dyCDCcmbfWlLkFGMZ3N5mGil8fK36dA2zO89/Nw8BS%0Anv9ulhbnq75HJSjOaWlr+0REDETEcVT+5XszvpdO8CXgysy8tu58T7ybvvmCtEm2HTAArKw7v5LK%0AX3Jqj+qf/WjvZeeaMo+Mcu8j+O4mRfGNx2cDP8rMpcXpHYB1mfl4XfHa/2Z2oO7dZebjEbEO380m%0AiYh9qYSKLYAngbdk5t0RsT++l7YpAt8cKsNY9XrivxlDxqap3y41RjmnqTfRexntHfnuJs8Xgf2o%0AjBFPxHczNX5BZe7R1lTG7P9PRLx2nPK+lxaLiJcBXwD+PDPXlLmVLno3Dpc0ZxWVcbD6pLg9G/8r%0AWlNnRfHreO9lBfCSUe59Mb67TRYR5wJvBl6XmQ/WXFoBTI+IbepuqX83z3t3RfnN8d1sksxcl5m/%0AzszbMnMBlcnTH8b30k5zqPw5L4mIZyPiWSoTqD9U/H4lPfBuDBlNyMx1wBIqs+hrzQVumvoWqbCM%0Ayn90z72XYv7Ma/nje7kZGIqIg2rK/BmVOQS+uyYVS4e/CLwVODIzl9UVWQI8w/PfzSxgH57/bvYp%0Azlf9OZUvhFrSqrb3qaAybu97aZ/vA/tS6WGqHrcBX6v5ffe/m3bPPO3WAziWyszf46msWDiHyljn%0Azu1uWy8fVGZiV/+DTOCU4vezi+sfpbKa5C1U/mP8OvAwMLOmjquo/Evu4OK4E7i83Z+tmw/gy8Wf%0A+2up/MuqemxZU+Z/AQ8AR1FZ9v194A5goLg+ANwFXFtcP6oof267P183H8D/AA4HdqHyl9qZVHpi%0A5/peOuugZnVJr7ybtjegmw9gPnAff0yNr2l3m3r9AI4owkX98dXiegCfoLKUdQ2VlSX71NWxLXAx%0AMFIcFwNbt/uzdfMxxjtJ4N01ZbYAzgUeBf4AXA68rK6e2cAVxfVHi/Iz2v35uvkAFtX8/9QjxV9I%0Ac30vnXeMEjK6/t34Ve+SJKklnJMhSZJawpAhSZJawpAhSZJawpAhSZJawpAhSZJawpAhSZJawpAh%0ASZJawpAhSZJawpAhSZJawpAhSZJawpAhSZJawpAhSZJa4v8HAsHUCUw7seoAAAAASUVORK5CYII=" alt="" />
- 机器学习算法整理(二)梯度下降求解逻辑回归 python实现
逻辑回归(Logistic regression) 以下均为自己看视频做的笔记,自用,侵删! 还参考了:http://www.ai-start.com/ml2014/ 用梯度下降求解逻辑回归 Logi ...
- 斯坦福机器学习视频笔记 Week1 线性回归和梯度下降 Linear Regression and Gradient Descent
最近开始学习Coursera上的斯坦福机器学习视频,我是刚刚接触机器学习,对此比较感兴趣:准备将我的学习笔记写下来, 作为我每天学习的签到吧,也希望和各位朋友交流学习. 这一系列的博客,我会不定期的更 ...
- Andrew Ng机器学习公开课笔记 -- 线性回归和梯度下降
网易公开课,监督学习应用.梯度下降 notes,http://cs229.stanford.edu/notes/cs229-notes1.pdf 线性回归(Linear Regression) 先看个 ...
- 线性回归、梯度下降(Linear Regression、Gradient Descent)
转载请注明出自BYRans博客:http://www.cnblogs.com/BYRans/ 实例 首先举个例子,假设我们有一个二手房交易记录的数据集,已知房屋面积.卧室数量和房屋的交易价格,如下表: ...
- 线性回归和梯度下降代码demo
程序所用文件:https://files.cnblogs.com/files/henuliulei/%E5%9B%9E%E5%BD%92%E5%88%86%E7%B1%BB%E6%95%B0%E6%8 ...
- Machine Learning--week2 多元线性回归、梯度下降改进、特征缩放、均值归一化、多项式回归、正规方程与设计矩阵
对于multiple features 的问题(设有n个feature),hypothesis 应该改写成 \[ \mathit{h} _{\theta}(x) = \theta_{0} + \the ...
- Andrew Ng机器学习算法入门(三):线性回归算法
线性回归 线性回归,就是能够用一个直线较为精确地描述数据之间的关系.这样当出现新的数据的时候,就能够预测出一个简单的值. 线性回归中最常见的就是房价的问题.一直存在很多房屋面积和房价的数据,如下图所示 ...
- 机器学习算法整理(七)支持向量机以及SMO算法实现
以下均为自己看视频做的笔记,自用,侵删! 还参考了:http://www.ai-start.com/ml2014/ 在监督学习中,许多学习算法的性能都非常类似,因此,重要的不是你该选择使用学习算法A还 ...
- 2018.4.23-ml笔记(线性回归、梯度下降)
线性回归:找到最合适的一条线来最好的拟合我们的数据点. hθ(x) = θixi=θTx θ被称之为权重参数 θ0为拟合参数 对每个样本yi=θTxi + εi 误差ε是独立并且具有 ...
随机推荐
- MAVEN ERROR maven-resources-plugin
maven新建项目时报错 Could not calculate build plan: Plugin org.apache.maven.plugins:maven-resources-plugin: ...
- 【转】 MATLAB下如何指定GPU资源
[转] MATLAB下如何指定GPU资源 原文链接
- 《TCP/IP 详解 卷1:协议》第 8 章:Internet 控制报文协议
路由器是 Internet 的重要组成部分,严密监视 Internet 的操作.IP 协议未给发送失败的 IP 数据包提供一种错误处理,也没有给端系统提供直接的方法来发现错误.为了解决这一不足之处,I ...
- 团队作业2 <嗨,你的快递!>需求分析与原型设计
哦,不,是你的快速(*_*) 第一部分 需求分析 1.1 用户调研 1.1.1调研对象:由于我们的系统是校园快递代取业务,面向的是大学生活,所以本次调研范围都是在校大学生(除了师大学生,也包括了外校的 ...
- poi excel导入 数字自动加小数点
问题:导入excel表,若表格中为整数数字,不管单元格设置成数字格式还是文本格式,导入时都会出现小数点和0. 我遇到的问题是:一个名称,做测试数据的时候做了纯整形数字,发现了这个问题. 解决办法:在代 ...
- 弹出提示框的方式——java
1.显示一个错误对话框,该对话框显示的 message 为 'alert': JOptionPane.showMessageDialog(null, "alert", " ...
- 二叉查找树ADT--C语言描述
首先给出此ADT的声明: struct TreeNode; typedef struct TreeNode *Position; typedef struct TreeNode *SearchTree ...
- vue-cli配置axios
1. npm install axios --save 2. npm install @type/axios --save-dev(使用ts编写的需要此声明文件,升级的axios好像不需要了,已经自带 ...
- Memcache介绍与应用场景
一:概念介绍 Memcache是一个高性能的分布式的内存对象缓存系统,通过在内存里维护一个统一的巨大的hash表,它能够用来存储各种格式的数据,包括图像.视频.文件以及数据库检索的结果 ...
- springcloud微服务实战:Eureka+Zuul+Feign/Ribbon+Hystrix Turbine+SpringConfig+sleuth+zipkin
相信现在已经有很多小伙伴已经或者准备使用springcloud微服务了,接下来为大家搭建一个微服务框架,后期可以自己进行扩展.会提供一个小案例: 服务提供者和服务消费者 ,消费者会调用提供者的服务,新 ...







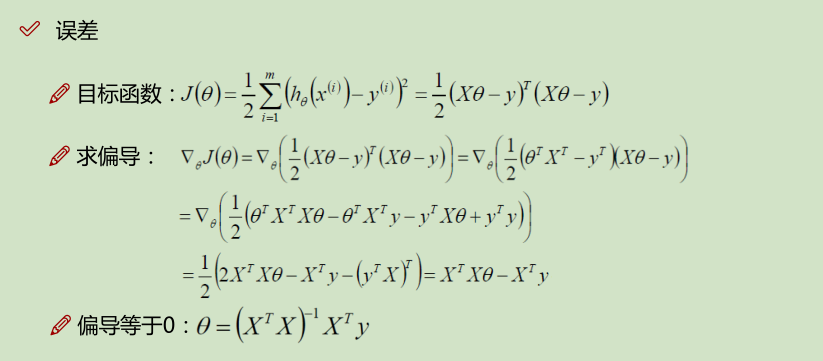





 (theta_0, theta_1同时更新)
(theta_0, theta_1同时更新)


