P2054 [AHOI2005]洗牌

题目描述

为了表彰小联为Samuel星球的探险所做出的贡献，小联被邀请参加Samuel星球近距离载人探险活动。

由于Samuel星球相当遥远，科学家们要在飞船中度过相当长的一段时间，小联提议用扑克牌打发长途旅行中的无聊时间。玩了几局之后，大家觉得单纯玩扑克牌对于像他们这样的高智商人才来说太简单了。有人提出了扑克牌的一种新的玩法。

对于扑克牌的一次洗牌是这样定义的，将一叠N（N为偶数）张扑克牌平均分成上下两叠，取下面一叠的第一张作为新的一叠的第一张，然后取上面一叠的第一张作为新的一叠的第二张，再取下面一叠的第二张作为新的一叠的第三张……如此交替直到所有的牌取完。

如果对一叠6张的扑克牌1 2 3 4 5 6，进行一次洗牌的过程如下图所示：

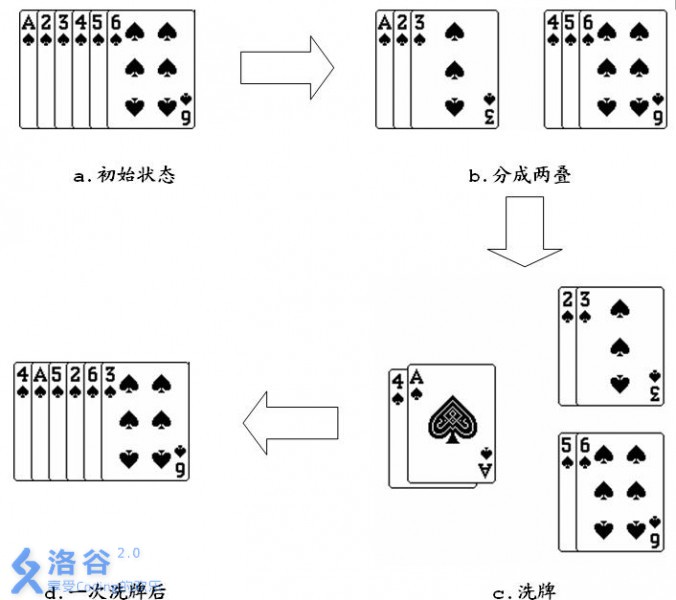
从图中可以看出经过一次洗牌，序列1 2 3 4 5 6变为4 1 5 2 6 3。当然，再对得到的序列进行一次洗牌，又会变为2 4 6 1 3 5。

游戏是这样的，如果给定长度为N的一叠扑克牌，并且牌面大小从1开始连续增加到N（不考虑花色），对这样的一叠扑克牌，进行M次洗牌。最先说出经过洗牌后的扑克牌序列中第L张扑克牌的牌面大小是多少的科学家得胜。小联想赢取游戏的胜利，你能帮助他吗？

输入输出格式

输入格式：

输入文件中有三个用空格间隔的整数，分别表示N，M，L

（其中0＜N≤10^10 ，0 ≤M≤10^10，且N为偶数）。

输出格式：

单行输出指定的扑克牌的牌面大小。

错误日志：弄错了通解的周期周期为 $\frac{b}{gcd(a,b)}$

Solution

对于一张牌 $x$（初始位于 $x$ 这一位置），我们发现他轮换一次可以到达 $(x * 2) \% (n + 1)$ 的位置

所以轮换 $m$ 次可以到达 $(x * 2^{m}) \% (n + 1)$ 这一位置

我们设这个位置为 $p$（其实就是题目给出的 $L$）

这题实际上求解的就是 $x$ 满足 $x * 2^{m} \equiv L (Mod\ n + 1)$

所以解上列同余方程即可

补充复习：

对于 $ax + by = c$

当 $gcd(a, b) | c$ 时存在解

其通解为 $x * \frac{c}{gcd(a,b)}+ k * \frac{b}{gcd(a,b)}, k \in Z^{+}$

Code

#include<iostream>

#include<cstdio>

#include<queue>

#include<cstring>

#include<algorithm>

#include<climits>

#define LL long long

using namespace std;

LL RD(){

    LL out = 0,flag = 1;char c = getchar();

    while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();}

    while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();}

    return flag * out;

    }

LL n, m, l;

LL x, y;

LL exgcd(LL a, LL b, LL &x, LL &y){

	if(b == 0){x = 1, y = 0;return a;}

	LL d = exgcd(b, a % b, x, y);

	LL temp = x;

	x = y, y = temp - a / b * y;

	return d;

	}

LL Q_pow(LL a, LL p, LL m){

	LL base = a, ans = 1;

	while(p){

		if(p & 1)ans *= base, ans %= m;

		base *= base, base %= m;

		p >>= 1;

		}

	return ans % m;

	}

int main(){

	n = RD();m = RD();l = RD();

	LL a = Q_pow(2, m, n + 1), b = n + 1, c = l;

	LL d = exgcd(a, b, x, y);

	x *= c;

	x = ((x % b) + b) % b;

	printf("%lld\n", x);

	return 0;

	}