内部排序->选择排序->堆排序
文字描述
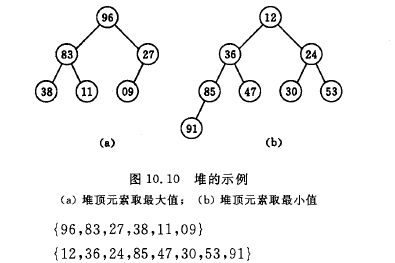
堆排序中,待排序数据同样可以用完全二叉树表示, 完全二叉树的所有非终端结点的值均不大于(或小于)其左、右孩子结点的值。由此,若序列{k1, k2, …, kn}是堆,则堆顶元素(或完全二叉树的根)必为序列中n个元素的最小值(或最大值)。
若在输出堆顶的最小值之后,使得剩余n-1个元素的序列重又建成一个堆,则得到n个元素中的次小值。如此反复执行,便能得到一个有序序列,这个过程称之为堆排序。
由此,实现堆排序需要解决两个问题:(1)如何由一个无序序列建成一个堆?(2)如何在输出堆顶元素之后,调整剩余元素成为一个新的堆?
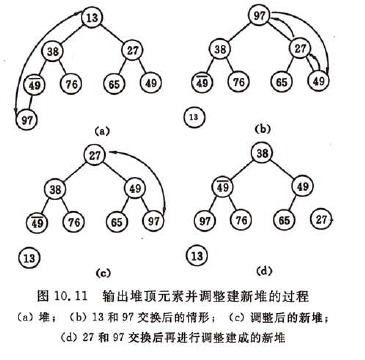
先讨论第(2)个问题,假设有个最大堆(堆顶元素为堆的最大值)输出堆顶元素之后, 以堆中最后一个元素代替之,此时根结点的左、右子树均为堆,则仅需自上至下进行调整即可。称这个自堆顶至叶子的调整过程为“筛选”。
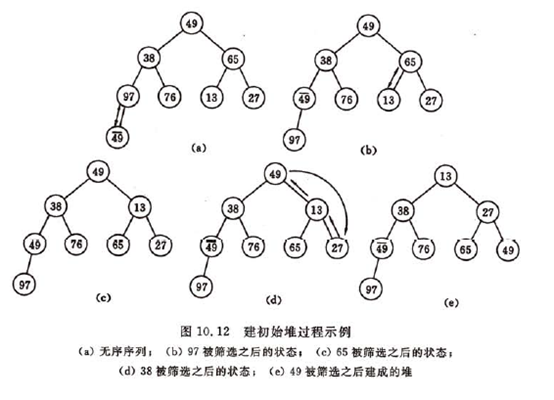
再讨论第(1)个问题,由一个无序序列建成堆的过程就是一个反复”筛选”的过程。若将此序列看成一个完全二叉树,则最后一个非终端结点是第[n/2]个元素,由此“筛选”只需从第[n/2]个元素开始。
示意图
算法分析
堆排序在树形选择排序上进行了改进, 和树形选择排序比, 堆排序可以减少辅助空间, 避免和”最大值”的冗余比较等优点.
堆排序在最坏情况下,其时间复杂度也为nlogn。相对于快速排序来说,这是堆排序的最大优点(快速排序最坏情况下时间复杂度为n*n, 但平均性能为nlogn)。
堆排序只需一个记录大小的辅助空间供交换用。
堆排序是一种不稳定的排序方法。
另外,堆排序方法对记录数较少的文件并不提倡使用, 但是对n较大的文件还是很有效的,因为其运行时间主要耗费在建立初始堆和调整新堆时的反复“筛选”上。
代码实现
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
/*
* double log2(double x); 以2为底的对数
* double ceil(double x); 取上整
* double floor(double x); 取下整
* double fabs(double x); 取绝对值
*/ #define DEBUG #define EQ(a, b) ((a) == (b))
#define LT(a, b) ((a) < (b))
#define LQ(a, b) ((a) <= (b)) #define MAXSIZE 100
#define INF 1000000
typedef int KeyType;
typedef char InfoType;
typedef struct{
KeyType key;
InfoType otherinfo;
}RedType; typedef struct{
RedType r[MAXSIZE+];
int length;
}SqList; void PrintList(SqList L){
int i = ;
printf("下标值:");
for(i=; i<=L.length; i++){
printf("[%d] ", i);
}
printf("\n关键字:");
for(i=; i<=L.length; i++){
if(EQ(L.r[i].key, INF)){
printf(" %-3c", '-');
}else{
printf(" %-3d", L.r[i].key);
}
}
printf("\n其他值:");
for(i=; i<=L.length; i++){
printf(" %-3c", L.r[i].otherinfo);
}
printf("\n\n");
return ;
} //堆采用顺序存储表示
typedef SqList HeapType; /*
*已知H->r[s,...,m]中记录的关键字除H->r[s].key之外均满足的定义
*本汉书调整H-r[s]的关键字,使H->r[s,...,m]成为一个大顶堆(对其中
*记录的关键字而言)
*/
void HeapAdjust(HeapType *H, int s, int m)
{
RedType rc = H->r[s];
int j = ;
//沿key较大的孩子结点向下筛选
for(j=*s; j<=m; j*=){
//j为key较大的纪录的下标
if(j<m && LT(H->r[j].key, H->r[j+].key))
j+=;
//rc应该插入位置s上
if(!LT(rc.key, H->r[j].key))
break;
H->r[s] = H->r[j];
s = j;
}
//插入
H->r[s] = rc;
} /*
* 对顺序表H进行堆排序
*/
void HeapSort(HeapType *H)
{
int i = ;
//把H->r[1,...,H->length]建成大顶堆
for(i=H->length/; i>=; i--){
HeapAdjust(H, i, H->length);
}
#ifdef DEBUG
printf("由一个无序序列建成一个初始大顶堆:\n");
PrintList(*H);
#endif
RedType tmp;
for(i=H->length; i>; i--){
//将堆顶记录和当前未经排序子序列H->r[1,...,i]中最后一个记录相互交换
tmp = H->r[];
H->r[] = H->r[i];
H->r[i] = tmp;
//将H->r[1,...,i-1]重新调整为大顶堆
HeapAdjust(H, , i-);
#ifdef DEBUG
printf("调整1至%d的元素,使其成为大顶堆:\n", i-);
PrintList(*H);
#endif
}
} int main(int argc, char *argv[])
{
if(argc < ){
return -;
}
HeapType H;
int i = ;
for(i=; i<argc; i++){
if(i>MAXSIZE)
break;
H.r[i].key = atoi(argv[i]);
H.r[i].otherinfo = 'a'+i-;
}
H.length = (i-);
H.r[].key = ;
H.r[].otherinfo = '';
printf("输入数据:\n");
PrintList(H);
//对顺序表H作堆排序
HeapSort(&H);
return ;
}
堆排序
运行
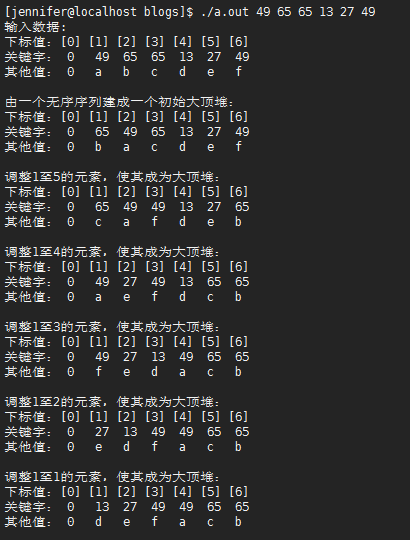
内部排序->选择排序->堆排序的更多相关文章
- 跳跃空间(链表)排序 选择排序(selection sort),插入排序(insertion sort)
跳跃空间(链表)排序 选择排序(selection sort),插入排序(insertion sort) 选择排序(selection sort) 算法原理:有一筐苹果,先挑出最大的一个放在最后,然后 ...
- 排序 选择排序&&堆排序
选择排序&&堆排序 1.选择排序: 介绍:选择排序(Selection sort)是一种简单直观的排序算法.它的工作原理如下.首先在未排序序列中找到最小(大)元素,存放到排序序列的起始 ...
- 内部排序->选择排序->树形选择排序
文字描述 树形选择排序又称锦标赛排序; 比如,在8个运动员中决出前3名至多需要11场比赛, 而不是7+6+5=18场比赛(它的前提是甲胜乙,乙胜丙,则甲必能胜丙) 首先对n个记录的关键字进行两两比较, ...
- 内部排序->选择排序->简单选择排序
文字描述 简单排序的基本思想是:每一趟在n-i+1(i=1,2,…,n)个记录中选取关键字最小的记录作为有序列表中的第i个记录. 示意图 略 算法分析 简单排序算法中,所需进行记录移动的操作次数较少, ...
- java实现 排序算法(鸡尾酒排序&选择排序&插入排序&二分插入排序)
1.鸡尾酒排序算法 源程序代码: package com.SuanFa; public class Cocktial { public static void main(String[] arg ...
- JAVA排序--[选择排序]
package com.array; public class Sort_Select { /** * 项目名称:选择排序 ; * 项目要求:用JAVA对数组进行排序,并运用选择排序算法; * 作者: ...
- C-冒泡排序,选择排序,数组
——构造类型 ->数组 ->一维数组 ->相同类型的一组数据 ->类型修饰符--数组名—[数组的元素个数(必须是整型表达式或者是整型常量,不能是变 ...
- 排序——选择排序(java描述)
百度百科的描述如下:选择排序(Selection sort)是一种简单直观的排序算法.它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后,再从剩余未排序元 ...
- [javaSE] 数组(排序-选择排序)
两层嵌套循环,外层循环控制次数,内层循环进行比较 for(int x=0;x<arr.length;x++){ for(int y=0;y<arr.length;y++){ if(arr[ ...
随机推荐
- 传统D3D11程序面向VS2015编译环境的配置修正细节
A. 配置细节 使用#include <unordered_map>替代<hash_map> 这个是c++标准建议的,没啥好说的 使用#include <directx ...
- 树莓派raspi2-ubuntu meta安装配置指导
首先是硬件准备: 1.树莓派raspi2B------------------------1 2.普通显示器----------------------------1 3.普通pc---------- ...
- 【emWin】例程二十六:窗口对象——Listbox
简介: 列表框用于选择列表的一个元素.创建的列表框可以没有环绕的框架窗口,或者作为 FRAMEWIN 小工具的子窗口建立列表框中的项目被选定后,会突出显示. 触摸校准(上电可选择是否进入校准界面) 示 ...
- 【原】为DevExpress的ChartControl添加Y轴控制 和 GridControl中指定列添加超级链接
一.控制ChartControl的Y轴范围 使用Devexpress中的CharControl控件,需要控制AxisY轴的显示范围,需要使用该控件的BoundDataChanged事件,具体代码如下: ...
- Fixed Partition Memory Management UVALive - 2238 建图很巧妙 km算法左右顶点个数不等模板以及需要注意的问题 求最小权匹配
/** 题目: Fixed Partition Memory Management UVALive - 2238 链接:https://vjudge.net/problem/UVALive-2238 ...
- 《FPGA全程进阶---实战演练》第七章 让按键恢复平静
1基础理论部分 A:“怎么按键按下去之后,结果不正常?”,B:“按键你消抖了吗?”A:“消什么抖,还要消抖?”, B:“先检测按键变化,然后消抖过滤波动信号,最后输出稳定信号”,A:“我好像漏掉了什 ...
- Java8学习笔记(六)--Optional
前言 身为一名Java程序员,大家可能都有这样的经历:调用一个方法得到了返回值却不能直接将返回值作为参数去调用别的方法.我们首先要判断这个返回值是否为null,只有在非空的前提下才能将其作为其他方法的 ...
- VBA 根据Find方法根据特定内容查找单元格
http://club.excelhome.net/thread-940744-1-1.html 2. Find方法的语法[语法]<单元格区域>.Find (What,[After],[L ...
- hosts文件配置不生效的解决办法
分析可能的原因并给出相应的解决方案. 第一 种情况,在开启浏览器的时候修改磁盘上的hosts文件,比如说加了原先没有的一句"127.0.0.1 www.360.cn",保存host ...
- IDEA导入springboot项目不能启动
由于工具没有识别到项目的pom.xml文件,所以需要在右侧的Maven栏目中点击 + 号,选中项目的pom.xml文件,则导入成功.
