高斯混合模型 GMM

本文将涉及到用 EM 算法来求解 GMM 模型，文中会涉及几个统计学的概念，这里先罗列出来：

• 方差：用来描述数据的离散或波动程度.

\[var(X) =  \frac{\sum_{i=1}^N( X_i-\bar{X})^2}{N-1}\]

• 协方差：协方差表示了变量线性相关的方向，取值范围是 $[-\infty, +\infty]$，一般来说协方差为正值，说明一个变量变大另一个变量也变大；取负值说明一个变量变大另一个变量变小，取0说明两个变量没有相关关系.

\[cov(X,Y) =  \frac{\sum_{i=1}^N( X_i-\bar{X})(Y_i-\bar{Y}) }{N-1}\]

• 相关系数：协方差可反映两个变量之间的相互关系及相关方向，但无法表达其相关的程度，皮尔逊相关系数不仅表示线性相关的方向，还表示线性相关的程度，取值$[-1,1]$，也就是说，相关系数为正值，说明一个变量变大另一个变量也变大；取负值说明一个变量变大另一个变量变小，取0说明两个变量没有相关关系，同时，相关系数的绝对值越接近1，线性关系越显著。

\[\rho_{XY} = \frac{cov(X,Y)}{\sqrt{DX}\sqrt{DX}}\]

• 协方差矩阵： 当 $X \in \mathbb{R}^n$ 为高维数据时，协方差矩阵可以很好的反映数据的性质，在协方差矩阵中，对角线元素反映了数据在各个维度上的离散程度，协方差矩阵为对角阵，非对角线元素反映了数据各个维度的相关性，其形式如下：

\[\mathbf{\Sigma} = \begin{bmatrix}
cov(x_1,x_1) &  cov(x_1,x_2)&\cdots  &cov(x_1,x_n) \\ cov(x_2,x_1) &  cov(x_1,x_1)&\cdots  &cov(x_1,x_1) \\
\vdots & \vdots   & &  \vdots & \\ cov(x_n,x_1) &  cov(x_n,x_1)&\cdots  &cov(x_n,x_n) 
\end{bmatrix}\]

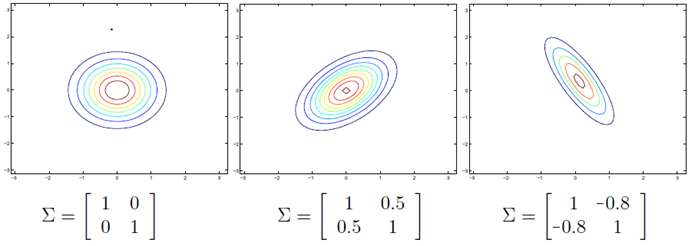
上图展示了二维情况下，使用不同的协方差矩阵时高斯分布的变化，左边代表不相关，中间为正相关，右边为负相关。

高斯分布

假设数据 $\mathbf{x} \in \mathbb{R}^n$ 服从参数为 $\mathbf{\mu},\mathbf{\Sigma}$ 的高斯分布:

\[ \mathcal{N}(\mathbf{x};\mu,\mathbf{\Sigma}) = \frac{1}{(2\pi)^{n/2}|\mathbf{\Sigma}|^{1/2}}\exp\left \{ -\frac{1}{2} (\mathbf{x}-\mu)^T\mathbf{\Sigma}^{-1}(\mathbf{x}-\mu) \right \}\]

这里 $\mu$ 为均值， $\Sigma$ 为协方差矩阵，对于单个高斯分布，当给定数据集之后，直接进行 MLE 即可估计高斯分布的参数；但是有些数据集是多个高斯分布叠加在一起形成的，也就数据集是由多个高斯分布产生的，如下图所示三个高斯分布叠加在一起：

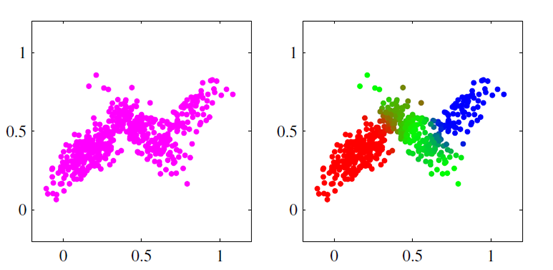
多个高斯分布叠加在一起便是混合高斯模型 GMM，GMM 的定义如下：

\[p(\mathbf{\mbox{x}}) = \sum_{k=1}^K \pi_k \mathcal{N}(\mathbf{\mbox{x}} | \mathbf{\mu}_k, \mathbf{\Sigma}_k)\]

这里 $K$ 表示高斯分布的个数， $\pi_k$ 代表 mixing coefficient ，且满足 $0 \le \pi_k \le 1,\sum_k\pi_k = 1$，其实这里 $p(\mathbf{x})$ 表示为 $K$ 个高斯分布的加权， $\pi_k$ 就是权重系数，如果把 GMM 用在聚类中，则样本 $\mathbf{x}$ 的类别即为 $\arg\max_k\pi_k$.

在 GMM 中，需要估计的参数为 $\pi_k， \mu_k， \mathbf{\Sigma}_k$，模型里每个观测数据 $\mathbf{x}$ 都对应着一个隐变量 $\mathbf{z} \in \mathbb{R}^K$，代表的即为类别变量， 且 $\mathbf{z}_k \in \left \{  0,1\right \}$ ，一个样本可以属于多个类别，叠加起来概率为 1 ，这里显而易见有：

\[p(\mathbf{z}_k = 1) = \pi_k \]

则第 $k$ 个高斯分布可以表示为：

\[p(\mathbf{\mbox{x}}|z_k = 1) = \mathcal{N}(\mathbf{\mbox{x}} | \mathbf{\mu}_k, \mathbf{\Sigma}_k)\]

如果已知 $\mathbf{x}$ 所属的分布 $k$ ，则可把上式写成向量形式：

\[p(\mathbf{x}|\mathbf{z}) = \mathcal{N}(\mathbf{\mbox{x}} | \mathbf{\mu}_k, \mathbf{\Sigma}_k)\]

因此完全数据的密度函数为：

\[p(\mathbf{\mbox{x}}) = \sum_{\mathbf{\mbox{z}}} p(\mathbf{\mbox{z}}) p(\mathbf{\mbox{x}} | \mathbf{\mbox{z}}) = \sum_{k=1}^K \pi_k \mathcal{N}(\mathbf{\mbox{x}} | \mathbf{\mu}_k, \mathbf{\Sigma}_k)\]

单个样本推倒完成，接下来给定观测数据集 $X$，对应的完全数据集为 $\left\{ X,Z\right\}$ ，此时 $Z$ 是不可见的，形式如下：

\[X = \begin{bmatrix} - \mathbf{x}_1^T-\\ -\mathbf{x}_2^T -\\  \vdots \\ -\mathbf{x}_N^T -\\\end{bmatrix} \ \ Z = \begin{bmatrix} - \mathbf{z}_1^T-\\ -\mathbf{z}_2^T -\\ \vdots \\ -\mathbf{z}_N^T -\\\end{bmatrix}\]

对于该 GMM 的参数就采用 EM 算法来求解了，完全数据的联合分布为：

\[p(\mathbf{X,Z} | \mathbf{\mu, \Sigma, \pi}) = \prod_{n=1}^N \left \{ \sum_{k=1}^K \pi_k \mathcal{N}(\mathbf{\mbox{x}}_n \vert \mathbf{\mu}_k, \mathbf{\Sigma}_k) \right \}\]

写成对数似然函数的形式：

\[\ln p(\mathbf{\mbox{X,Z}} | \mathbf{\mu, \Sigma, \pi}) = \sum_{n=1}^N \ln \left \{ \sum_{k=1}^K \pi_k  \mathcal{N}(\mathbf{\mbox{x}}_n | \mathbf{\mu}_k, \mathbf{\Sigma}_k)  \right \}\]

下面便是EM 算法求解 GMM 的过程：

E步： 使用参数 $\theta^{old}=(\pi^{old},\mu^{old},\mathbf{\Sigma}^{old})$ ，计算每个样本 $x_n$ 对应隐变量 $z_n$ 的后验分布：

\begin{aligned}
\gamma(z_{nk})=p(z_n = k|\mathbf{x}_n;\mathbf{\mu}^{old},\mathbf{\Sigma}^{old})
&=\frac{p(z_{nk} = 1)p(\mathbf{x_{nk}}|z_{nk} = 1)}{\sum_{j=1}^Kp(z_{nj} = 1)p(\mathbf{x_n}|z_{nj} = 1)}\\
&= \frac{ \pi_k^{old} \mathcal{N}(\mathbf{\mbox{x}}_n | \mathbf{\mu}_k^{old}, \mathbf{\Sigma}_k^{old})} {\Sigma_{j=1}^K\pi_j^{old} \mathcal{N}(\mathbf{\mbox{x}}_n | \mathbf{\mu}_j^{old}, \mathbf{\Sigma}^{old}_j)}
\end{aligned}

M步：便是极大化 Q 函数的计算，这里 Q 函数有非常漂亮的形式：

\begin{aligned}
\mathcal{Q} (\mathbf{\theta}, \mathbf{\theta}^{\mbox{old}}) 
&=  \sum_{Z} p(Z | X,\theta^{old}) \ln p(X, Z | \theta)\\
&=  \sum_{Z} p(Z | X,\theta^{old}) \ln p(X| Z ,\theta)P(Z|\theta)\\
&=\sum_{n= 1}^N \sum_{k=1}^K\gamma(z_{nk})\left \{  \ln \pi_k +\ln\mathcal{N}(\mathbf{x}_n|\mathbf{\mu}_k ,\mathbf{\Sigma}_k) \right \}\\
\end{aligned}

得到下一步迭代的参数：

\[\theta^{new}=\arg\max_{\theta}\mathcal{Q} (\mathbf{\theta}, \mathbf{\theta}^{\mbox{old}})  \]

对 Q 函数求导，另倒数得 0 ，即可求得下一次迭代的参数值，这里省去计算过程，只给出结果：

\begin{aligned}
\mathbf{\mu}_k^{new} &= \frac{1}{N_k}\sum_{n=1}^N\gamma(z_{nk})\mathbf{x}_n\\
\mathbf{\Sigma}_k^{new} &= \frac{1}{N_k}\sum_{n=1}^N\gamma(z_{nk})(\mathbf{x}_n-\mathbf{\mu}_k^{new})(\mathbf{x}_n-\mathbf{\mu}_k^{new})^T \\
\mathbf{\pi}_k^{new} &=  \frac{N_k}{N}
\end{aligned}

其中：

\[N_k = \sum_{n=1}^N \gamma(z_{nk})\]

这便是完整的 GMM 推倒过程，理解的不是很好，有机会继续深入。

参考：

Pattern Reconginition and Machine Learning

http://www.zhihu.com/question/20852004

http://www.cnblogs.com/nsnow/p/4758202.html

http://alexkong.net/2014/07/GMM-and-EM/

http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html

http://www.cnblogs.com/ooon/p/5787995.html