CH 2601 - 电路维修 - [双端队列BFS]

题目链接：传送门

描述

Ha'nyu是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女Rika，从而被收留在地球上。Rika的家里有一辆飞行车。有一天飞行车的电路板突然出现了故障，导致无法启动。
电路板的整体结构是一个R行C列的网格（R,C≤500），如右图所示。每个格点都是电线的接点，每个格子都包含一个电子元件。电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。在旋转之后，它就可以连接另一条对角线的两个接点。电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

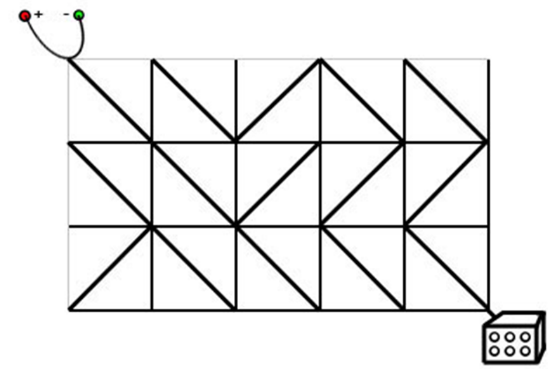
Ha'nyu发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。不过，电路的规模实在是太大了，Ha'nyu并不擅长编程，希望你能够帮她解决这个问题。

输入格式

输入文件包含多组测试数据。第一行包含一个整数 T 表示测试数据的数目。
对于每组测试数据，第一行包含正整数 R 和 C，表示电路板的行数和列数。
之后 R 行，每行 C 个字符，字符是"/"和"\"中的一个，表示标准件的方向。

输出格式

对于每组测试数据，在单独的一行输出一个正整数，表示所需的缩小旋转次数。
如果无论怎样都不能使得电源和发动机之间连通，输出NO SOLUTION。

样例输入

1
3 5
\\/\\
\\///
/\\\\

样例输出

1

数据范围与约定

对于40% 的数据，R,C≤5。
对于100% 的数据，R,C≤500，T≤5。

题解：

把网格的所有格点（横竖线交叉的点）看做无向图的节点，对于一个一个网格，它有两个对角节点。

假设这两个对角节点，已经有被方格里的短电线连接起来了，那么它们之间建立一条权值为 $0$ 的边；否则就建立权值为 $1$ 的边。

换句话说，这道题相当于：对于这样一张边权只为 $0$ 或 $1$ 的无向图，要求 $s \rightarrow t$ 的最短路。可以通过双端队列BFS完成。

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int INF=0x3f3f3f3f;

int r,c;
char mp[][];
inline int idx(int i,int j) {
    return i*(c+)+j;
}

struct Edge{
    int u,v,w;
    Edge(){}
    Edge(int _u,int _v,int _w){u=_u,v=_v,w=_w;}
};
vector<Edge> E;
vector<int> G[*];
void init(int l,int r)
{
    E.clear();
    for(int i=l;i<=r;i++) G[i].clear();
}
void addedge(int u,int v,int w)
{
    E.push_back(Edge(u,v,w));
    G[u].push_back(E.size()-);
}

int d[*],vis[*];
deque<int> Q;
int bfs(int s,int t)
{
    memset(d,0x3f,sizeof(d));
    memset(vis,,sizeof(vis));
    Q.push_back(s), d[s]=;
    while(!Q.empty())
    {
        int u=Q.front(); Q.pop_front();
        if(vis[u]) continue;
        else vis[u]=;
        for(int i=;i<G[u].size();i++)
        {
            Edge &e=E[G[u][i]]; int v=e.v;
            if(vis[v]) continue;
            if(d[v]>d[u]+e.w)
            {
                if(!e.w) Q.push_front(v);
                else Q.push_back(v);
                d[v]=d[u]+e.w;
            }
        }
    }
    return d[t];
}

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        scanf("%d%d",&r,&c);
        init(,idx(r,c));
        for(int i=;i<r;i++)
        {
            scanf("%s",mp[i]);
            for(int j=;j<c;j++)
            {
                if(mp[i][j]=='/')
                {
                    addedge(idx(i+,j),idx(i,j+),);
                    addedge(idx(i,j+),idx(i+,j),);
                    addedge(idx(i,j),idx(i+,j+),);
                    addedge(idx(i+,j+),idx(i,j),);
                }
                else
                {
                    addedge(idx(i,j),idx(i+,j+),);
                    addedge(idx(i+,j+),idx(i,j),);
                    addedge(idx(i+,j),idx(i,j+),);
                    addedge(idx(i,j+),idx(i+,j),);
                }
            }
        }

        int ans=bfs(idx(,),idx(r,c));
        if(ans==INF) printf("NO SOLUTION\n");
        else printf("%d\n",ans);
    }
}

一些后续：

代码是不是看着很眼熟？我自己敲着敲着都觉得我不是在敲双端队列BFS，我都以为是在敲优先队列优化Dijkstra……

其实这不是巧合，稍微思考一下就能明白，当我们边权仅为 $0$ 或 $1$ 时，其实不需要优先队列来帮我们控制队列里面每个状态的代价，我们自己就可以通过选择将状态从头部或者尾部push入队列来使得队列保持单调性（因为反正不管在什么时候，队列里面都只存在两种代价 $x$ 和 $x+1$）。

因此，每种状态虽然可能入队多次，但是第一次出队就已经是最小代价（vis标记该状态的最小代价已经求得），后续该状态再次出队直接忽略即可。类比于优先队列优化Dijkstra的时间复杂度，那么双端队列BFS的时间复杂度应当为 $O(|E|)$。

而在本题中，边数与 $RC$ 同阶，故本题双端队列时间复杂度 $O(RC)$。