梯度消失 / 梯度爆炸以及Xavier初始化
2018-12-06 16:25:08
首先我们先来看一下求解梯度的公式,以下面三层的网络为例:

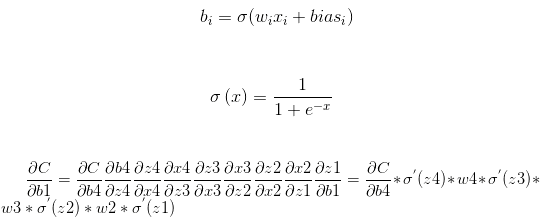
如果w初始化为大于1的数字,在深层神经网络计算梯度的时候就会出现梯度爆炸的现象;
如果w初始化为小于1的数字,在深层神经网络计算梯度的时候就会出现梯度消失的现象;
那么该如何初始化权重值呢?

z = w1 * x1 + w2 * x2 + ... + wn * xn
我们希望的是当n很大的时候,z的值不要过大。
其中一个方法就是通过修改方差的方法来完成这个操作,假设我们最初初始化的数值是N(0, 1)的标准正态分布,那么当n很大的时候我们希望w能更多的向0靠近,此时显然的我们需要方差进行减小,这里我们可以将方差设置为1 / n来完成相应的操作。具体的初始化公式如下:
w = np.random.randn(f_in, f_out) * np.sqrt(1 / n)
实验证明,当使用relu做为激活函数的时候,方差为2 / n效果更好,因此修正的Xavier初始化公式如下:
w = np.random.randn(f_in, f_out) * np.sqrt(2 / n)
梯度消失 / 梯度爆炸以及Xavier初始化的更多相关文章
- 梯度消失&&梯度爆炸
转载自: https://blog.csdn.net/qq_25737169/article/details/78847691 前言 本文主要深入介绍深度学习中的梯度消失和梯度爆炸的问题以及解决方案. ...
- LSTM如何解决梯度消失或爆炸的?
from:https://zhuanlan.zhihu.com/p/44163528 哪些问题? 梯度消失会导致我们的神经网络中前面层的网络权重无法得到更新,也就停止了学习. 梯度爆炸会使得学习不稳定 ...
- RNN梯度消失和爆炸的原因 以及 LSTM如何解决梯度消失问题
RNN梯度消失和爆炸的原因 经典的RNN结构如下图所示: 假设我们的时间序列只有三段, 为给定值,神经元没有激活函数,则RNN最简单的前向传播过程如下: 假设在t=3时刻,损失函数为 . 则对于一 ...
- [ DLPytorch ] 循环神经网络进阶&拟合问题&梯度消失与爆炸
循环神经网络进阶 BPTT 反向传播过程中,训练模型通常需要模型参数的梯度. \[ \frac{\partial L}{\partial \boldsymbol{W}_{qh}} = \sum_{t= ...
- [DeeplearningAI笔记]改善深层神经网络_深度学习的实用层面1.10_1.12/梯度消失/梯度爆炸/权重初始化
觉得有用的话,欢迎一起讨论相互学习~Follow Me 1.10 梯度消失和梯度爆炸 当训练神经网络,尤其是深度神经网络时,经常会出现的问题是梯度消失或者梯度爆炸,也就是说当你训练深度网络时,导数或坡 ...
- 梯度消失、梯度爆炸以及Kaggle房价预测
梯度消失.梯度爆炸以及Kaggle房价预测 梯度消失和梯度爆炸 考虑到环境因素的其他问题 Kaggle房价预测 梯度消失和梯度爆炸 深度模型有关数值稳定性的典型问题是消失(vanishing)和爆炸( ...
- L14梯度消失、梯度爆炸
梯度消失.梯度爆炸以及Kaggle房价预测 梯度消失和梯度爆炸 考虑到环境因素的其他问题 Kaggle房价预测 梯度消失和梯度爆炸 深度模型有关数值稳定性的典型问题是消失(vanishing)和爆炸( ...
- L8梯度消失、梯度爆炸
houseprices数据下载: 链接:https://pan.baidu.com/s/1-szkkAALzzJJmCLlJ1aXGQ 提取码:9n9k 梯度消失.梯度爆炸以及Kaggle房价预测 代 ...
- 神经网络优化算法:Dropout、梯度消失/爆炸、Adam优化算法,一篇就够了!
1. 训练误差和泛化误差 机器学习模型在训练数据集和测试数据集上的表现.如果你改变过实验中的模型结构或者超参数,你也许发现了:当模型在训练数据集上更准确时,它在测试数据集上却不⼀定更准确.这是为什么呢 ...
随机推荐
- os模块,os.path模块,subprocess模块,configparser模块,shutil模块
1.os模块 os表示操作系统该模块主要用来处理与操作系统相关的操作最常用的文件操作打开 读入 写入 删除 复制 重命名 os.getcwd() 获取当前执行文件所在的文件夹路径os.chdir(&q ...
- 2.Android硬件访问服务编写系统代码【转】
本文转载自:https://blog.csdn.net/qq_33443989/article/details/76696772 版权声明:本文为博主(Tower)自学笔记,欢迎转载! :-) ...
- linux基础之vim编辑器
vi : Visual Interface vim : VI Improved : VI的基础加上一些有用的插件 vim编辑器: 文本编辑器, 字处理器, 全屏编辑器, 模式化编辑器 vim的模式有三 ...
- tp剩余未验证内容-3
为什么有时候会 出现 "上传文件保存错误"? public function save($file, $replace=true){ /* 移动文件 */ if (!move_up ...
- P3178 [HAOI2015]树上操作
P3178 [HAOI2015]树上操作 思路 板子嘛,其实我感觉树剖没啥脑子 就是debug 代码 #include <bits/stdc++.h> #define int long l ...
- luogu1110[ZJOI2007]报表统计
思路 这里的初始化就不讲了,看完操作讲解就应该明白了,再不行就去看代码 对于操作1 由于操作2的需要,vector[n]存下数 对于操作2的维护 查询相邻两个元素的之间差值(绝对值)的最小值 先把所有 ...
- yum命令showduplicates安装指定版本包
默认情况下,我们用yum list 或者 yum install 的时候,yum会默认选择最新的版本. 如果我们需要安装指定版本的某个软件包,以使之能够和我们现有环境的软件包版本匹配,那么就需要用到s ...
- oracle 之 如何链接别人电脑的oracle
1.首先确保两台电脑是在同一个局域网内,可以通过cm命令窗口 ping 对方电脑的ID,若是没问题则表示可以连接 2.接下来通过配置来首先连接对方的电脑 其实在后面还有一个是否创建新的额服务名的操作, ...
- 51Nod—1174 区间中最大的数 线段树模版
在大佬们题解的帮助下算是看懂了线段树吧...在这mark下防一手转头就忘. #include<iostream> #include<stdio.h> using namespa ...
- HDU 3400 Line belt (三分套三分)
http://acm.split.hdu.edu.cn/showproblem.php?pid=3400 题意: 有两条带子ab和cd,在ab上的速度为p,在cd上的速度为q,在其它地方的速度为r.现 ...
