Permutation Bo (数学证明)

当在两端时：共有n * (n - 1)种组合，满足条件的有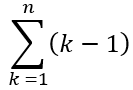，计算可得， counter = n * (n - 1) / 2。

其他位置时：共有n * (n - 1) * (n - 2) 种组合，满足条件的有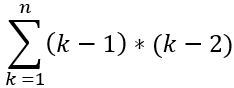，利用平方和公式计算可得counter = n * (n - 1) * (n - 2)  / 3。

#include<bits/stdc++.h>
using namespace std;

int main()
{
    int n;
    while(~scanf("%d",&n))
    {
        double ans = 0.0, c;
        for(int i=;i<=n;i++){
            scanf("%lf", &c);
            if(i ==  || i == n) ans += c/2.0;
            else ans += c/3.0;
        }
        printf("%lf\n",n == 1 ? c : ans);
    }
    return ;
}