2020牛客寒假算法基础集训营1 F-maki和tree

链接：https://ac.nowcoder.com/acm/contest/3002/F
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

有一天，maki拿到了一颗树。所谓树，即没有自环、重边和回路的无向连通图。
这个树有 个顶点， 条边。每个顶点被染成了白色或者黑色。
maki想知道，取两个不同的点，它们的简单路径上有且仅有一个黑色点的取法有多少？
注：
①树上两点简单路径指连接两点的最短路。
② 和 的取法视为同一种。

 

 

 

输入描述:

第一行一个正整数n。代表顶点数量。

第二行是一个仅由字符'B'和'W'组成的字符串。第 i个字符是B代表第 i 个点是黑色，W代表第 i个点是白色。

接下来的n-1行，每行两个正整数 x ， y，代表 x 点和 y点有一条边相连 

输出描述:

一个正整数，表示只经过一个黑色点的路径数量。

示例1

输入

复制

3
WBW
1 2
2 3

输出

复制

3

说明

树表示如下：

其中只有2号是黑色点。

<1,2>、<2,3>、<1,3>三种取法都只经过一个黑色点。

 

思路：

　　　对于可以连边的白色节点，用并查集把节点合并，并且在合并时更新连通块大小。

　　　对于一条含有黑色节点的路径，我们易知：路径数 = 黑色节点相邻的 白连通块内点的size * 该点相连的白连通块点的size···

　　　

　　　所以只需要先求出白连通块的大小，然后对于黑点，只需要计算出黑点相邻白连通块加上其的后继连通块即可。

　　　后继白连通块大小求法：

　　　

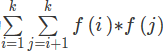
　　　关于_find中为什么是sum += sz[r2]的问题，因为建的是无向图，不保证此时的fa[r1]一定是与fa[r2]相等的

　　

 #include <bits/stdc++.h>
 #define dbg(x) cout << #x << "=" << x << endl
 
 using namespace std;
 typedef long long LL;
 const int maxn = 1e6 + ;
 
 int n;
 LL ans;
 int fa[maxn];
 int a[maxn];
 int head[maxn];
 char c[maxn];
 int cnt = ;
 LL sz[maxn];
 LL num[maxn];
 int _count = ;
 
 //vector <int> g[maxn];
 
 struct Edge {
     int to,nxt;
 }edge[maxn];
 
 void BuildGraph(int u, int v) {
     edge[cnt].to = v;
     edge[cnt].nxt = head[u];
     head[u] = cnt++;
 
     edge[cnt].to = u;
     edge[cnt].nxt = head[v];
     head[v] = cnt++;
 }
 
 void init()
 {
     memset(head, -, sizeof(head));
     for(int i = ; i <= n; i++) {
         fa[i] = i;
         sz[i] = ;
     }
 }
 
 namespace _buff {
     const size_t BUFF =  << ;
     char ibuf[BUFF], *ib = ibuf, *ie = ibuf;
     char getc() {
         if (ib == ie) {
             ib = ibuf;
             ie = ibuf + fread(ibuf, , BUFF, stdin);
         }
         return ib == ie ? - : *ib++;
     }
 }
 
 int read() {
     using namespace _buff;
     int ret = ;
     bool pos = true;
     char c = getc();
     for (; (c < '' || c > '') && c != '-'; c = getc()) {
         assert(~c);
     }
     if (c == '-') {
         pos = false;
         c = getc();
     }
     for (; c >= '' && c <= ''; c = getc()) {
         ret = (ret << ) + (ret << ) + (c ^ );
     }
     return pos ? ret : -ret;
 }
 
 int fid(int x)
 {
     int r = x;
     while(fa[r] != r) {
         r = fa[r];
     }
     int i,j;///路径压缩
     i = x;
     while(fa[i] != r) {
         j = fa[i];
         fa[i] =  r;
         i = j;
     }
     return r;
 }
 
 void join(int r1,int r2)///合并
 {
     int fidroot1 = fid(r1), fidroot2 = fid(r2);
     int root = min(fidroot1, fidroot2);
     sz[root] = sz[fidroot1] + sz[fidroot2];
     if(fidroot1 != fidroot2) {
         fa[fidroot2] = root;
         fa[fidroot1] = root;
     }
 }
 
 LL _find(int x) {
     //dbg(x);
     LL sum = ;
     for(int i = head[x]; ~i; i = edge[i].nxt) {
         int v = edge[i].to;
         if(a[v]) {
             //num[v] = 0;
             continue;
         }
         int r1 = fid(x), r2 = fid(v);
         sum += sz[r2];
         num[++_count] = sz[r2];
     }
     return sum;
 }
 
 int main()
 {
     scanf("%d\n",&n);
     init();
     ans = ;
     scanf("%s",c);
     for(int i = ; i < n; ++i) {
         if(c[i] == 'W') {
             a[i+] = ;
         }
         else {
             a[i+] = ;
         }
     }
     for(int i = ; i < n; ++i) {
         int x, y;
         scanf("%d %d",&x, &y);
         BuildGraph(x,y);
         if(!a[x] && !a[y]) {
             join(x,y);
         }
     }
     for(int i = ; i <= n; ++i) {
         if(a[i] == ) continue;
         _count = ;
         memset(num, , sizeof(num));
         ans += _find(i);
         for(int j = ; j <= _count; ++j) {
             for(int k = j+; k <= _count; ++k) {
                 ans += num[j] * num[k];
             }
         }
     }
 
     printf("%lld\n",ans);
 }