Tarjan算法——强连通、双连通、割点、桥

Tarjan算法

概念区分

• 有向图
  • 强连通：在有向图\(G\)中，如果两个顶点\(u, v\ (u \neq v)\)间有一条从\(u\)到\(v\)的有向路径，同时还有一条从\(v\)到\(u\)的有向路径，则称\(u, v\)强连通
  • 强连通图：如果有向图\(G\)的任意两个不同的顶点都强连通，则称\(G\)是一个强连通图
  • 强连通分量：有向图\(G\)的极大强连通子图称为图\(G\)的强连通分量
• 无向图
  • 连通：和强连通类似(只是无向图的任意边都是双向的，如果存在\(u\rightarrow v\)的路径，必然存在\(v\rightarrow u\)的路径)
  • 连通图：如果无向图\(G\)的任意两不同的顶点都连通，则称\(G\)是一个连通图
  • 连通分量：无向图\(G\)的极大连通子图称为图\(G\)的连通分量
  • 割点(割顶)：在无向图\(G\)中，如果删除一个点\(u\)及以\(u\)为端点的所有边后，图的连通分量个数增多，则称点\(u\)为割点(割顶)
  • 桥：在无向图\(G\)中，如果删除一条边$e=(u,v)\ \((连接\)u,v\(两点的边)后，图的连通分量个数增多，则称边\)e$为桥，也称割边
  • 双连通：
    • 双连通图：分为点双连通图和边双连通图，若一个无向图\(G\)中的去掉任意一个节点(一条边)都不会改变图\(G\)的连通性，即不存在割点(桥)，则称图\(G\)点(边)双连通图
    • 边双连通图：一个无向图\(G\)中的每一个极大点双连通子图和边双连通子图分别称为无向图\(G\)的点双连通分量(BCC)和边双连通分量(e-BCC)

Tarjan

DFS​树

\(tarjan\)的过程实际上就是一个\(dfs\)的过程，对图\(G\)进行\(dfs\)会得到一棵\(dfs\)树，在有向图的\(dfs\)树中有四种边，树边、回边(返祖边、后向边)、横叉边和前向边。树边顾名思义，回边是指在\(dfs\)过程中搜索到已经访问过的点，但它的子树未访问完成；横叉边是指搜索到已经访问过的点且它的子树也已访问完成，而且横叉边连接的两个点不是祖先和后代的关系；前向边与横叉边唯一的不同在于前向边连接的两个点是祖先和后代的关系，读者可以结合下图理解这四种边

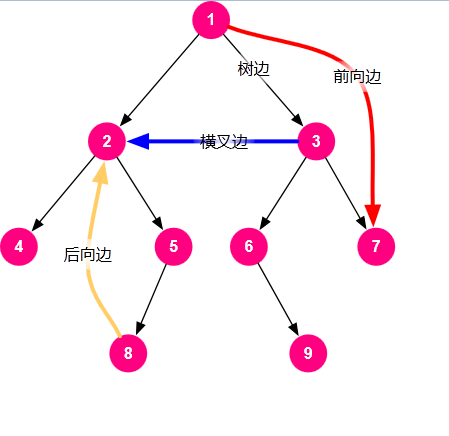
⏫图片来源：https://www.cnblogs.com/gongpixin/p/5003049.html

强连通分量

思想

• \(dfn[u]\)：顶点\(u\)被访问到的时间戳，每个点的\(dfn\)被赋值后就不会改变

• \(low[u]\)：顶点\(u\)能够到达的点中的\(dfn\)最小值

• \(stack[top]\)：可能构成强连通分量的点的集合

• \(vis[u]：\)顶点\(u\)是否在栈中

• \(color[u]\)：顶点\(u\)的颜色，用于区分不同的强连通分量

  // 有些题目添加\(color\)数组比较方便，不是必要的

采用深度优先搜索的思想，对每一个可能的强连通分量进行\(dfs\)：维护一个可能构成强连通分量的集合\(stack\)，将搜索到的点加入\(stack\)，并维护其\(dfn,\ vis\)值，往下搜它的边连接的顶点，在回溯的时候维护\(low\)的值，如果点\(u\)的\(dfn==low\)说明它是某个强连通分量子树的根，此时我们找到了一个强连通分量，只要将栈\(stack\)中的点弹出，直到弹出\(u\)

• 同一个强连通分量中的点的\(low\)值是相同的

看到这儿，有些读者可能会问，那无向图的连通分量咋求？也是直接套\(tarjan\)的板子吗？如果您有这样困惑反正我是有过，那是学算法学傻了不是，无向图还\(tarjan\)啥，直接\(dfs\)或\(bfs\)一遍就完了，那善于思考的读者们又会问了，为啥无向图这么方便？因为对于无向图，如果存在路径\(u\rightarrow v\)，那路径\(v\rightarrow u\)必然存在，\(u\)能跑到的点(包括\(u\)自己)都是一个连通分量里的

板子

有向图强连通分量

void tarjan(int u) {
	dfn[u] = low[u] = ++tim;
	vis[u] = true; // 入栈
	stack[++top] = u;
	int size = g[u].size();
	for(int i = 0; i < size; ++i) {
		int v = g[u][i];
		if(!dfn[v]) { // 树边，继续下搜
			tarjan(v);
			low[u] = min(low[u], low[v]);
		} else if(vis[v]) // 回边，更新low[u]
            low[u] = min(low[u], dfn[v]);
	}
	if(dfn[u] == low[u]) {
		color[u] = ++sum;
		vis[u] = false;
		while(stack[top] != u) {
			color[stack[top]] = sum;
			vis[stack[top--]] = false;
		}
		top--;
	}
}

//for(int i = 1; i <= n; ++i)
//    if(!dfn[i])
//        tarjan(i);

割点(顶) / 桥

原理

在\(tarjan\)算法求割点的过程中，主要涉及到两种边：树边和回边(返祖边)，意义已在上文中提到⏫

• 定理\(1\)：在无向图\(G\)中，点\(u(u不是根节点)\)是割点 \(\iff\) \(u\)的某个子树\(T\)中不含有返回\(u\)的祖先(不包括\(u\))的边 \(\iff\) \(low[v] >= dfn[u]\)

  特别地，根节点是割顶 \(\iff\) 它的子节点数目大于\(1\)

  画图YY一下：

  

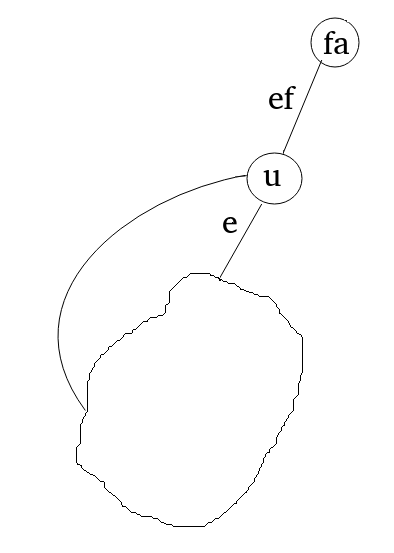
  上图的\(u\)的某个子树\(T\)中虽然有返回\(u\)的回边，但是没有返回\(u\)的祖先(不包含\(u\))的回边，所以\(u\)是割点，但是边\(e\)并不是桥

• 定理\(2\)：在无向图\(G\)中，边\((u,v)\)是桥 \(\iff\) \(u\)的某个子树\(T\)中不含有返回\(u\)的祖先(包括\(u\))的边 \(\iff\) \(low[v] > dfn[u]\)

  还是看之前的图，\(fa\)的某个子树中不含有返回\(fa\)的祖先(包括\(fa\))的回边，所以\(ef\)是桥

• 可以看出如果一个图\(G\)有桥，它必有割点，因为桥连接的两端必然至少有一个是割点，但反过来不成立

板子

还有点细节：

\(child\)是点\(fa\)的子节点个数，注意\(fa\)的孙子不计算在内

特别的，像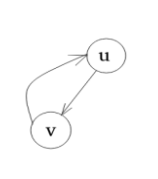：，点\(u\)不是割点，因为去掉它后，这个图的强连通分量的个数并没有增加

void Tarjan(int u, int fa) { // 割点
    low[u] = dfn[u] = ++tim;
    int sz = g[u].size(), child = 0;
    for(int i = 0; i < sz; i++) {
        int v = g[u][i];
        if(!dfn[v]) {
            Tarjan(v, fa);
            low[u] = min(low[v], low[u]);
            if(low[v] >= dfn[u] && u != fa) iscut[u] = true;
			// if(low[v] > dfn[u]) u - v 是桥
            if(u == fa) child++;
        } else
            low[u] = min(low[u], dfn[v]);
    }
    if(fa == u && child >= 2) iscut[u] = true;
}

//for(int i = 1; i <= n; ++i)
//    if(!dfn[i])
//        tarjan(i, i);

缩点

啥是缩点

就把一个强连通分量(或边双连通分量等，视题目而定)缩成一个点

再看张图YY一下：

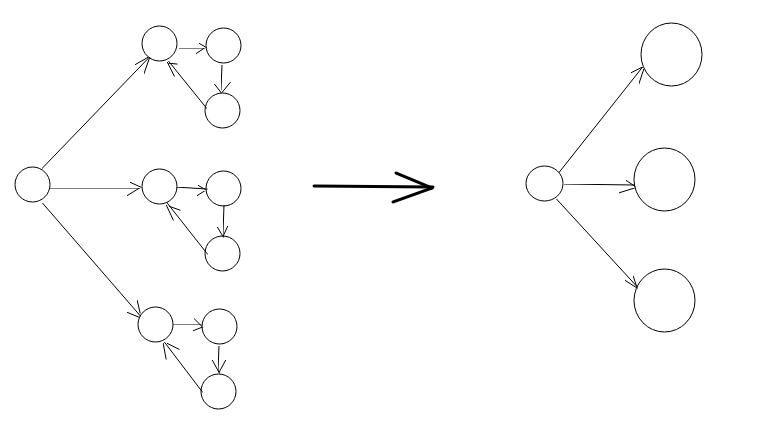
光这么讲，大家肯定还是云里雾里，这缩点到底能干啥？下面我们通过两道例题来看看缩点到底能干啥

例题

• 洛谷P3387 缩点

  思路：缩点，把一个强连通分量缩成一个点，新点的权值等于强连通分量里的所有点的点权之和，缩完点就能得到一个有向无环图\((DAG)\)，然后就可以在这个\(DAG\)上跑\(dp\)了，然后就能得到答案

双连通分量

一点性质

• 边双连通分量(e-BCC)满足任意两点间都有至少两条边不重复的路径
• 点双连通分量(BCC)满足任意两点间都有至少两条点不重复路径
• 有桥必有割点，一个点双连通分量必然是边双连通分量，反之，不一定成立

边双连通分量(e-BCC)

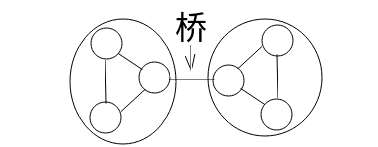
如上图，左右两个用大圈圈出来的分别是两个边双连通分量

求法：

把桥全部去掉剩下的独立的分量都是边双连通分量，所以只要一遍\(tarjan\)找到桥，再一遍\(dfs\)就能能求出边双连通分量

点双连通分量(BCC)

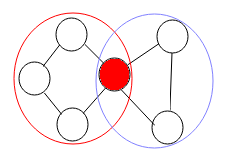
如上图，左边红圈圈出的和紫色圈圈出的分别是两个点双连通分量，红点是整张图的一个割点

两个点双连通分量间至多有一个公共点，且它一定是割点；不是割点的点，一定属于某个点双连通分量

求法：

只要分离了割点，就可以把点双连通分量分离出来，但是一个割点可能同属于两个点双连通分量，所以一般用分量中的边来输出，可以用栈保存遍历到的边，一旦发现割顶就弹出属于一个BCC的边

例题

• POJ3352 Road Construction

  思路：题意是问最少加几条边可以使整个图变成边双连通的，即问最少加多少条边可以使整张图的任意两点间至少有两条边不重复路径，所以我们可以将已有的边双连通分量缩点，缩完点形成一棵树。现在，题目变为在缩完点后的树上最少添加几条边能使其变为边双连通图，有一个结论是对于一棵无向树,我们要使得其变成边双连通图，需要添加的边数= (树上度数为1的点的个数+1)/2