清北学堂—2020.1提高储备营—Day 2 morning（并查集、堆）

qbxt Day 2 morning

——2020.1.18 济南 主讲：李佳实

目录一览

1.并查集
2.堆

总知识点：基础数据结构

一、并查集

1.描述：并查集是一类十分常用的数据类型，它有着十分广泛的应用。在信息竞赛中，它主要执行的操作一般有三种。
（1） 合并a,b两个元素所在的集合 Merge(a,b)
（2）查找某个元素属于哪个集合 find(k)
（3）查询两个元素是否属于同一集合 Query(a,b)
2.函数模板
（1）find

int find(int x){
    if(fa[x]==x) return x;   //找到即返回
    int t=find(fa[x]);  //继续递归find
    return t;
} 

（2）Merge

void merge(int x,int y){
    x=find(x);
    y=find(y);
    if(x==y) return;    //根相同，无需合并，即返回
    fa[x]=y;    //根不同，即合并
}

3.对于find和merge的优化
（1）
对于merge：启发式合并（使用次数少）
描述：在合并集合S1、S2的时候，我们让较小的树成为较大的树的子树。这里可以是深度、节点个数等启发函数来比较树的大小（一般使用深度）。
代码实现会使用到并查集，而且并不常用，暂且略。
（2）
对于find：路径压缩（常用，效率高，代码简单）
描述：我们在查找完u至根节点的路径之后，一般将这条路径上的所有节点的父节点都设为根节点，这样可以大大减少之后的查找次数。
代码；

int find(int x){
    if(fa[x]==x) return x;
    int t=find(fa[x]);
    fa[x]=t;    //记录路径上的节点成为父节点，减少查询次数
    return t;
}

（3）时间复杂度分析：
可以证明，经过启发式合并和路径压缩之后的并查集，执行m次查找的复杂度为O(mα(m))
注α(m)：Ackermann函数的某个反函数，可以近似的认为它是小于5的。所以并查集的单次查找操作的时间复杂度也几乎是常数级的。

4.例题:
（1）[Noi2015]程序自动分析
题目描述：
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本：假设x1,x2,x3,…代表程序中出现的变量，给定n个形如xi=xj或xi≠xj的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：x1=x2，x2=x3，x3=x4，x1≠x4，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。
现在给出一些约束满足问题，请分别对它们进行判定。
注：1≤n≤1000000
样例：

分析：这个题核心思想就是：看输入的是1，我们把它加到一个并查集里去，是0，我们暂且不管。操作好以后，我们特判是0，但树根相同的这种情况，显然是不成立的。标记下来，一个个输出就结束了。
代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define N 1000010
using namespace std;
int fa[N];
int find(int x) //寻找函数
{
    if(fa[x]==x) return x;
    int t=find(fa[x]);
    fa[x]=t;
    return t;
    //return fa[x]==x?x:fa[x]=find(fa[x]);
}
void merge(int x,int y) // 合并函数
{
    x=find(x);
    y=find(y);
    if(x==y) return;
    fa[x]=y;
}
int m,x[N],y[N],f[N];
void doit()
{
    memset(fa,0,sizeof(fa));    //记得清空
    for(int i=1;i<=1000000;i++) fa[i]=i;    //初始化
    cin>>m;
    for(int i=1;i<=m;i++)
    {
        cin>>x[i]>>y[i]>>f[i];
        if(f[i]==1) merge(x[i],y[i]);   // 合并
    }
    bool ans=true;
    for(int i=1;i<=m;i++)
    {
        if(f[i]==0)
        {
            if(find(x[i])==find(y[i])) ans=false;   //如果在一个并查集里，但不是1，那就显然不成立，进行标记
        }
    }
    puts(ans?"YES":"NO");
}
int main()
{
    int T;
    cin>>T;
    while(T--) doit();
}

二、堆

1.描述：堆的物理结构就是数组，堆的逻辑结构是一棵完全二叉树。树中每个结点与数组中存放该结点中值的那个元素相对应。如下图：

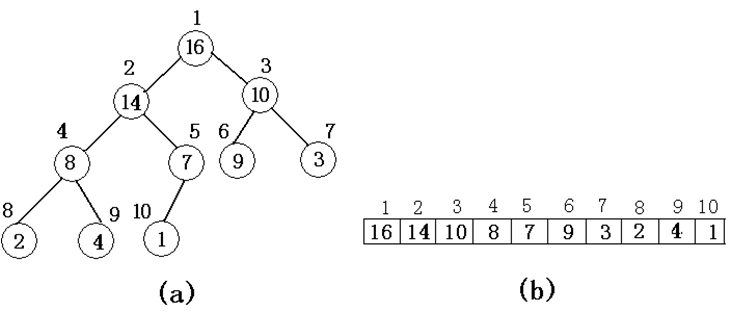
2.性质
（1）若节点x的两儿子为y，z，且x的编号为i。则y（左儿子）为2i，z（右儿子）为2i+1。
（2）对于大顶堆（小顶堆对称考虑）来说（根节点是全局最大值），每个节点的值都大于等于它的儿子节点的值。
3.基本操作
（1）up（即上浮操作）
思想：当小根堆的元素值h[x]变小时，该结点可能会上浮，如果h[x]小于h[x /2]则交换两个结点的值，如此循环下去直到x = 1或h[x] ≥ h[x /2]。
代码：

void up(int x){
    while(x>1){
        int y=x/2;    //x的左儿子
        if(a[y]>a[x]){    //比较编号
            swap(a[x],a[y]);
            x=y;    //直接覆盖
        }
        else break;
    }
}

（2）down（即下沉操作）
思想：当小根堆的元素值h[x]变大时，该结点可能会下沉，如果有儿子结点值小于该结点的值则跟较小儿子结点交换，如此循环下去直到条件不满足或者没有儿子结点。
代码：

void down(int x){
    while(x*2<=n){
        int y=x*2;
        if(x*2+1>n){    //不确定右儿子的有无，需判断
                                //这里为没有右儿子
            if(a[y]<a[x]){
                swap(a[x],a[y]);
                x=y;
            }
            else break;
        }
        else{        //有右儿子
            int z=y+1;       //右儿子编号为2i+1，左儿子为2i，右儿子=左儿子+1
            if(a[y]<a[z]){
                if(a[y]<a[x]){
                    swap(a[x],a[y]);
                    x=y;
                }
                else break;
            }
            else{
                if(a[z]<a[x]){
                    swap(a[x],a[z]);
                    x=z;
                }
                else break;
            }
        }
    }
}

（3）insert（即插入操作）
思想：插入一个元素，把该元素放在最后，再做up操作。
代码：

void insert(int x){
    a[++n]=x;
    up(n);
}

（4）delete（即删除操作）
思想：删除第x个元素，为了不破坏堆的性质，把h[len]移到x处，堆元素个数len减一，再判断做up(x)还是down(x)。
代码:

void del(int x){
    a[x]=a[n];    //放
    n--;     //减空间
        //判断up还是down
    if(x!=1&&a[x]<a[x/2]) up(x);
    else down(x);
}

4.例题
（1）堆排序
题目描述：使用堆完成n个整数的排序操作
分析：先用build把输入数组A[1…n]建成一个大根堆。因为数组中最大元素在根A[1],可以通过把它与A[n]互换来达到最终正确的位置，然后把堆的元素个数减1，再通过down(1)操作把剩下的n - 1个元素调整成大根堆，如此反复执行n - 1次。(O(nlogn))
代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define N 1000010
using namespace std;
int n,a[N];
void up(int x)
{
    while(x>1)
    {
        int y=x/2;
        if(a[y]>a[x])
        {
            swap(a[x],a[y]);
            x=y;
        }
        else break;
    }
}
void down(int x)
{
    while(x*2<=n)
    {
        int y=x*2;
        if(x*2+1>n)
        {
            if(a[y]<a[x])
            {
                swap(a[x],a[y]);
                x=y;
            }
            else break;
        }
        else
        {
            int z=y+1;
            if(a[y]<a[z])
            {
                if(a[y]<a[x])
                {
                    swap(a[x],a[y]);
                    x=y;
                }
                else break;
            }
            else
            {
                if(a[z]<a[x])
                {
                    swap(a[x],a[z]);
                    x=z;
                }
                else break;
            }
        }
    }
}
void insert(int x){
    a[++n]=x;
    up(n);
}
void del(int x){
    a[x]=a[n];
    n--;
    if(x!=1&&a[x]<a[x/2]) up(x);
    else down(x);
}
void build()    //建堆
{
    for(int i=n/2;i;i--) down(i);
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    build();
    int m=n;    //提前记录n值，因为这个值会被后面的操作改变
    for(int i=1;i<=m;i++)
    {
        int x=a[1];
        del(1);    //删堆顶
        cout<<x<<' ';
    }
    cout<<endl;
}

--------------------------------------------THE　END-------------------------------------------------