Luogu P1073 最优贸易(最短路)

P1073 最优贸易

题意

题目描述

\(C\)国有\(n\)个大城市和\(m\)条道路，每条道路连接这\(n\)个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这\(m\)条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为\(1\)条。

\(C\)国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到\(C\)国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设\(C\)国\(n\)个城市的标号从\(1 \sim n\)，阿龙决定从\(1\)号城市出发，并最终在\(n\)号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有\(n\)个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来\(C\)国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设\(C\)国有\(5\)个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

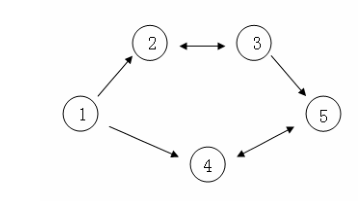
假设\(1 \sim n\)号城市的水晶球价格分别为\(4,3,5,6,1\)。

阿龙可以选择如下一条线路：\(1\)->\(2\)->\(3\)->\(5\)，并在\(2\)号城市以\(3\)的价格买入水晶球，在\(3\)号城市以\(5\)的价格卖出水晶球，赚取的旅费数为\(2\)。

阿龙也可以选择如下一条线路\(1\)->\(4\)->\(5\)->\(4\)->\(5\)，并在第\(1\)次到达\(5\)号城市时以\(1\)的价格买入水晶球，在第\(2\)次到达\(4\)号城市时以\(6\)的价格卖出水晶球，赚取的旅费数为\(5\)。

现在给出\(n\)个城市的水晶球价格，\(m\)条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入输出格式

输入格式：

第一行包含\(2\)个正整数\(n\)和\(m\)，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行\(n\)个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这\(n\)个城市的商品价格。

接下来\(m\)行，每行有\(3\)个正整数\(x,y,z\)，每两个整数之间用一个空格隔开。如果\(z=1\)，表示这条道路是城市\(x\)到城市\(y\)之间的单向道路；如果\(z=2\)，表示这条道路为城市\(x\)和城市\(y\)之间的双向道路。

输出格式：

一个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出\(0\)。

输入输出样例

输入样例：

5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2

输出样例：

5

说明

【数据范围】

输入数据保证\(1\)号城市可以到达\(n\)号城市。

对于\(10 \%\)的数据，\(1≤n≤6\)。

对于\(30 \%\)的数据，\(1≤n≤100\)。

对于\(50 \%\)的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于\(100 \%\)的数据，\(1 \leq n \leq 100000\)，\(1 \leq m \leq 500000\)，\(1 \leq x\)，\(y \leq n\)，\(1 \leq z \leq 2\)，\(1 \leq\)各城市水晶球价格\(\leq 100\)。

\(NOIP \ 2009\)提高组 第三题

思路

分层图板子题贼简单。 --huyufeifei

其实这题跟分层图没有半点关系，直接跑最短路就好了。

首先要看能从起点走到哪里，然后我们就可以选个最便宜地方来买水晶球；然后要看能从哪里走到终点，然后我们就可以选个最贵的地方来卖水晶球。这样，我们就可以枚举每个点，看最多能赚取的路费。

而查找这样的点时，我们可以用最短路算法，利用点权来松弛点权，这和边权的松弛操作是类似的。详情就看我漂亮的代码了。

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> PII;
const int MAXN=1e5+5;
const int MAXM=1e6+5;
int n,m,ans,a[MAXN],d[MAXN],__d[MAXN];
int cnt,top[MAXN],to[MAXM],nex[MAXM];
int __cnt,__top[MAXN],__to[MAXM],__nex[MAXM];
bool v[MAXN],__v[MAXN];
int read()
{
    int re=0;
    char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) re=(re<<3)+(re<<1)+ch-'0',ch=getchar();
    return re;
}
void add_edge(int x,int y){to[++cnt]=y,nex[cnt]=top[x],top[x]=cnt;}
void __add_edge(int x,int y){__to[++__cnt]=y,__nex[__cnt]=__top[x],__top[x]=__cnt;}
void Dijkstra()
{
    memset(d,0x3f,sizeof d);
    d[1]=a[1];
    priority_queue<PII,vector<PII>,greater<PII> >Q;
    Q.push(make_pair(d[1],1));
    while(!Q.empty())
    {
        int now=Q.top().second;Q.pop();
        if(v[now]) continue;
        v[now]=true;
        for(int i=top[now];i;i=nex[i])
            if(!v[to[i]])
            {
                d[to[i]]=min(d[now],a[to[i]]);
                Q.push(make_pair(d[to[i]],to[i]));
            }
    }
}
void __Dijkstra()
{
    __d[n]=a[n];
    priority_queue<PII>Q;
    Q.push(make_pair(__d[n],n));
    while(!Q.empty())
    {
        int now=Q.top().second;Q.pop();
        if(__v[now]) continue;
        __v[now]=true;
        for(int i=__top[now];i;i=__nex[i])
            if(!__v[__to[i]])
            {
                __d[__to[i]]=max(__d[now],a[__to[i]]);
                Q.push(make_pair(__d[__to[i]],__to[i]));
            }
    }
}
int main()
{
    n=read(),m=read();
    for(int i=1;i<=n;i++) a[i]=read();
    while(m--)
    {
        int x=read(),y=read(),z=read();
        add_edge(x,y),__add_edge(y,x);
        if(z==2) add_edge(y,x),__add_edge(x,y);
    }
    Dijkstra();
    __Dijkstra();
    for(int i=1;i<=n;i++) ans=max(ans,__d[i]-d[i]);
    printf("%d",ans);
    return 0;
}