Abaqus 子模型法 和 子结构法

目录

• 1 子模型法
  • 1.2 子模型法应用考虑因素
  • 1.3 子模型法关键技术
    • 1.3.1 单元选择
    • 1.3.2 驱动变量
    • 1.3.3 链接整体模型和子模型
  • 1.4 仿真过程
    • 1.4.1 问题描述
    • 1.4.2 整体分析
    • 1.4.3 基于面的子模型法
    • 1.4.3 基于节点的子模型法
• 2 子结构法
  • 2.1 为什么使用子结构
  • 2.2 子结构应用类型
• 参考资料

简单来说，子模型法是对感兴趣的区域进行放大，对网格进行细化，并采用位移或者力从整体模型的结果传递到子模型中。子结构法是将整体模型中的同类部件或者区域进行打包封装。

1 子模型法

• 子模型是得到模型部分区域中更加精确解的有限单元技术。在有限元分析中往往出现这种情况，即对于用户关心的区域，如应力集中区域，网格太疏不能得到满意的结果，而对于这些区域之外的部分，网格密度已经足够了。要得到这些关注区域的精确的解，可以采取两种办法：(a)用较细的网格重新划分并分析整个模型；（b)只在关心的区域细化网格并对其分析 ，显而易见，方法a太耗费机时，方法b即为子模型技术。
• 子模型是在全局模型分析结果的基础上研究局部模型的方法。通过初始的全局模型分析计算来确定在激励载荷作用下的最大响应区域，子模型方法不需要细化或重分析整体模型，只需截取局部关注区域模型并细化其网格从而提高分析精度。即采用粗网格模型得到局部关注区域周围的结果，采用局部区域网格细化得到局部分析结果。
• Abaqus中可以非常通用的添加子模型，为子模型定义的材料响应可以不同于整体模型定义的材料响应。
• Abaqus提供两种子模型技术：基于节点的子模型技术与基于面的子模型技术。

• 子模型法是基于Saint-Venant's 定理，要求子模型边界足够远离子模型响应的关注区域。因为建立子模型时没有一个明确的限制来保证结果有意义，因此需要用户自己判断子模型建立的正确性。如何判断子模型建立的正确性，一般的方法是查看子模型边界附近的结果变量值及云图变化与全局模型是否一致，如果结果一致，则认为该子模型是有效的。

  1.1 子模型法的分类

• 基于节点的子模型：使用全局模型节点位移结果场（包括位移、温度等）插值到子模型边界节点的技术，它能够得到相对更精确的位移结果，适用于任何分析类型；
• 基于面的子模型技术：将整体模型的结果插值到受驱动的基于单元的面片上的子模型积分点。

• 可使用线性和非线性分析过程的组合，不能用于一个导入的分析。

1.2 子模型法应用考虑因素

• 基于面的子模型仅对于实体模型和静态分析是可用的
• 整体模型刚度与子模型刚度相当时，两种方法的计算结果相当；当刚度相差较大时，通常基于面的子模型具有更加精确的应力结果。
• 基于点的子模型可对模型的大变形和转动进行更加精确的传递。
• 整体模型的位移与期望的子模型中位移密切对应时，基于节点的子模型通常是优先的；当子模型的位移响应不同于整体模型时，应使用基于面的子模型。（当模拟热-应变分析时，并且子模型的温度变化过程不同于整体模型时，可发生此种情况。例如，当热传到子模型做为顺序热-结构分析的一部分来执行时。）
• 基于面的子模型可以为刚度很大的结构提供更加精确的结果。
• 基于节点的子模型将产生一个位移场更加精确的传输；而就面的子模型将缠身各一个更加精确的应力场。
• 子模型不能参考一个包含多个载荷工况的整体模拟步，必须为将要驱动的子模型步使用一个单独的载荷定义，以执行整体分析。
• 子模型的维度必须和整体模型的维度保持一致

1.3 子模型法关键技术

1.3.1 单元选择

基于节点的子模型法：

• 二维模型
  实体-实体
  声学-结构
• 三维模型
  实体-实体
  壳-壳
  膜-膜
  壳-实体
  声学-结构

基于面的子模型法

• 二维模型
  实体-实体
• 三维模型
  实体-实体
• 注意：不支持圆柱形单元和连续的壳单元

1.3.2 驱动变量

1. 基于节点的位移做为驱动变量进行插值（较为常用）到子模型的边界
2. 基于面的应力作为驱动，使用应力场去插值子模型边界单元的高斯积分点处的应力

1.3.3 链接整体模型和子模型

子模型是做为整体分析的一个单独分析来运行的。子模型与整体模型之间的链接是将整体分析中保存的变量的时间相关值传递到子模型的相关边界节点上，或者传递到相关的边界面上。此传递是通过将来自整体模型的结果，为基于节点的子模型保存到结果文件（.fil）中，或者保存到输出数据文件（.odb）中，或者为基于应力的子模型保存到输出数据库文件（.odb）中，然后将这些结果读入子模型中分析。

1.4 仿真过程

1.4.1 问题描述

有一长条状的钢条，中间被钻了一个直径5mm的孔，试分析在左端固定，有端拉力500Pa状态下，孔周围的受力状态。采用子模型的方法。
弹性模量： 2.1E11 Pa
泊松比： 0.27
密度： 7800 kg/m3
屈服强度： 2.35E8 Pa

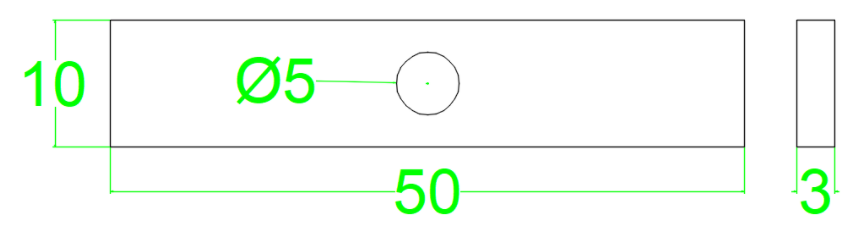
建立几何模型和材料赋值的过程省略。
先进行全域分析，然后进行子模型分析。

1.4.2 整体分析

网格划分
由于该模型不能直接进行结构化网格划分，需要对其进行分割，分割策略如下图所示，设置全局种子为1，进行网格划分。

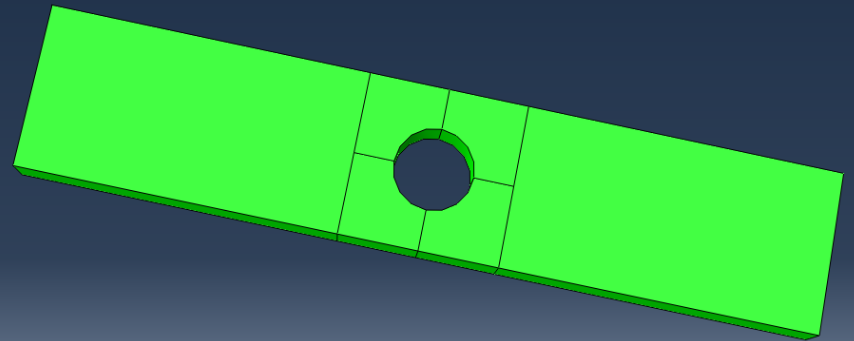
载荷边界设置
左端（-X端）固定，约束其X、Y、Z方向移动的自由度，在右端（+X端）施加500Pa的拉力。

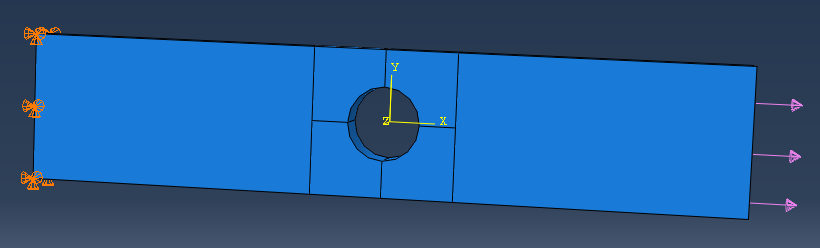
结果
其它情况默认，提交仿真获得的应力云图如下图所示。

1.4.3 基于面的子模型法

子模型创建
将上述的模型直接复制，生成子模型【Mode-2】，在左侧树状图中右键【Model-2】，在弹出的菜单中选择【Edit Attributes...】，在弹出的界面中选择【Submodel】，在【Read data from job:】后面输入整体模型的结果文件，此处为 “H:\Abaqus\SubModel\Job-1.odb”，如下图所示。（创建子模型并链接整体模型）

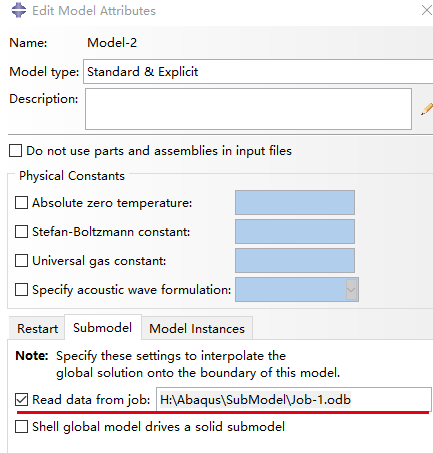
几何建模
取孔周围的一部分实体做为子模型，将复制过后的模型通过布尔运算，除去两端的部分，得到的图形如下图所示。材料设置和复制与整体模型保持一致。

定义子模型驱动面
点击【Create Load】图标，在弹出的窗口选择【Category--Other】，在【Types for Selected Step】中选择【Submodel】，点击按钮【Continue】；

然后选择子模型的周边的四个面（分割后八个面）作为驱动子模型的驱动面。（在任何步中，通过应力驱动的子模型的所有面，必须制定为驱动面，因为面的列表不能在它的初始定义之后进行扩展）

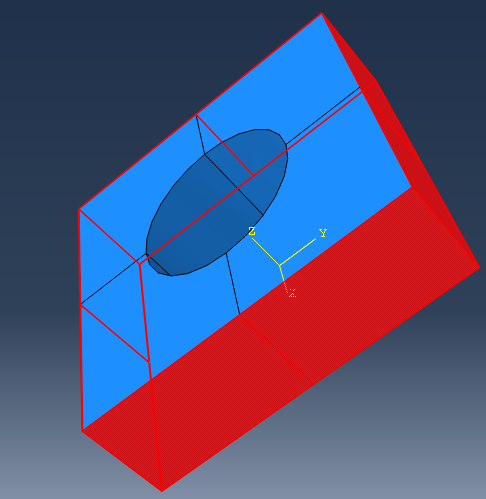
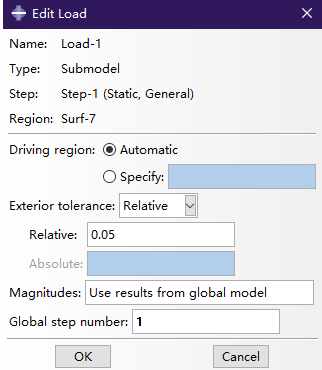
定义几何容差
当在整体中对面进行插值时，使用一个几何容差来定义子模型中单元的驱动面节点可以位于整体模型未变形的有限元模型外表面之外。默认情况下，子模型中的面节点，必须位于位于0.05倍整体模型中的平均单元大小距离之内。

指定步编号
指定整体模型历史的步，用于驱动当前子模型分析步骤的驱动变量

设置惯性释放
点击【Create Load】图标，在弹出的窗口选择【Category--Mechanical】，在【Types for Selected Step】中选择【Inertia relief】，点击按钮【Continue】，选择默认选项，点击确定。

结果
在求解之前，可以将求解精度设置为Full
设置其它必要的选项，然后提交求解，结果如下图所示。

1.4.3 基于节点的子模型法

子模型创建
将Model-2进行复制，创建Model-3模型。
由于是从Model-2复制的，所以该模型已经参考了整体模型的结果。

定义子模型中的驱动节点
删除Model-3中的载荷，其它内容不变。

• 指定驱动节点并不激活驱动变量，他们必须通过指定合适的子模型边界条件来激活。
• 在任何步中必须将驱动变量的子模型中的所有节点指定为驱动节点，因为节点的列表不能在初始定义之后进行拓展。
• 方法： 在载荷（Load）模块，电机【Create Boundary Condition】，在【Category】中选择【Other】，在【Types for Selected Step】中选择【Submodel】，然后点击确定；仍然选择上述四个面（分割后是八个面）作为驱动节点；在弹出的界面中，容差（Relative）保持默认值，自由度（Degrees of freedom）为子模型需要继承整体模型的节点自由度，这里填写“1,2,3”三个方向。整体模型中的分析步填写1，设置界面如下图所示。

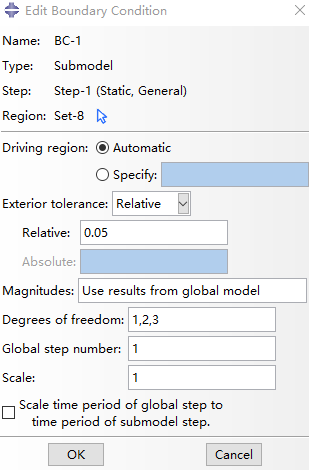
结果
创建分析步并求解，应力分析结果如下图所示。

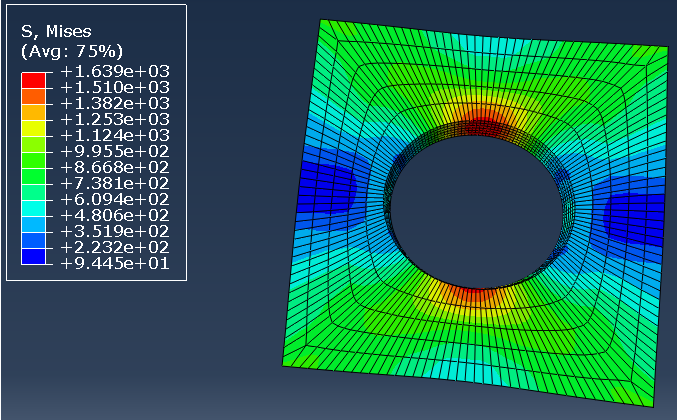
模型文件地址如下：
链接：https://pan.baidu.com/s/1-wtmiWmnyP35vpVE-FVzvw
提取码：ttbh

2 子结构法

• 子结构分析是一种用于简化计算时间的方法。当结构中某些部分为重复结构时，可以将其最小单元做为一个子结构单元，在实际分析时重复利用该单元。其另一种应用方法为，当对整体结构中的某微小部分进行局部设计时，可以见结构不变的部分做为一个子结构单元，在进行局部设计分析时也可重复利用该单元。
• 子结构的实现原理是将一组通过分块求解的方法把内部自由度消除，有时也称自由度凝聚。这样仅需对子结构进行一次刚度求解，对于重复次数较多的模型可以节约大量的计算时间。
• 通过保留节点上的保留自由度来与模型剩下的部分进行连接。
• Abaqus/CAE是不支持子结构的

2.1 为什么使用子结构

计算优势

• 做为子结构结果的刚度矩阵（刚度，质量）较小。
• 当多次使用相同的子结构时，效率得到提升。
• 子结构化可以隔离子结构以外的可能的外部变化，以解决分析过程时间。
• 在具有局部非线性的问题中，子结构将模型缩聚到只有在局部非线性中包含的自由度，则可以在一个非常低的自由度数量实现这些局部非线性的迭代。

组织优势

• 子结构为复杂分析系统了一个系统的解决方法。
• 子结构库允许分析间共享子结构。
• 许多实际结构非常庞大和复杂，以至于完结构的有限元模拟计算超出了可用的计算机资源，可以使用子结构进行结构优化，并一层一层的堆叠这些结构，知道完成整个结构，并且根据要求来局部回复位移和应力来解决。

将模型的局部作为一个整体来处理，缩聚其内部自由度，只保留与外部有连接关系的自由度，从而减小刚度矩阵和质量矩阵的规模和计算量。

2.2 子结构应用类型

可无限使用子结构：

• 静态应力分析
• 使用直接积分的隐式动力学分析
• 直接求解稳态动力学分析
• 固有频率提取
• 复特征值提取
• 基于模态的稳态动力学分析

子结构不支持恢复已经消除的自由度：

• 瞬态模拟动力学分析
• 响应谱分析
• 随机响应分析

参考资料

【1】基于Abaqus的子模型热固耦合
【2】Abaqus子模型简介
【3】学习Abaqus子模型从这里开始
【4】《Abaqus分析用户手册--分析卷》
【5】《Abaqus分析用户手册--指定条件、约束与相互作用卷》