简单DP内容

1.　　最长上升子序列

【题目描述】

给定N个数，求这N个数的最长上升子序列的长度。

【样例输入】

7

2 5 3 4 1 7 6

【样例输出】

4

第一种解法：时间复杂度O(n^2)，

状态设计：DP[ i ]代表以A[ i ]结尾的LIS的长度

状态转移：DP[ i ]=max{ DP[ j ]+1 ，DP[ i ] }(1<=j< i,A[j]< A[i])。

基本上思想，每次碰到一个数，就从头遍历，看插在哪个后面的值最大就保留那一个。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = ;
int a[maxn],dp[maxn];
int n,ans=-;
int main()
{
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&a[i]);
        dp[i]=;
    }
    for(int i=;i<=n;i++)
        for(int j=;j<i;j++)
            if(a[j]<a[i]) dp[i]=max(dp[i],dp[j]+);
    for(int i=;i<=n;i++)
        ans=max(ans,dp[i]);
    printf("%d\n",ans);
    return ;
}

第二种解法：时间复杂度O(nlogn)，优化在查询的时候。我们新建一个dp数组，dp[i]表示长度为 i 的LIS结尾元素的最小值。对于一个上升子序列，显然其结尾元素越小，越有利于在后面接其他的元素，也就越可能变得更长。因此，我们只需要维护dp数组，对于每一个a[i]，如果a[i] > dp[当前最长的LIS长度]，就把a[i]接到当前最长的LIS后面，即dp[++当前最长的LIS长度]=a[i]。 否则，就用a[i]取更新dp数组。具体方法是，在dp数组中找到第一个大于等于a[i]的元素dp[j]，用a[i]去更新dp[j]。如果从头到尾扫一遍dp数组的话，时间复杂度仍是O(n^2)。我们注意到dp数组内部一定是单调不降的，所有我们可以二分dp数组，找出第一个大于等于a[i]的元素。二分一次dp数组的时间复杂度的O(logn)，所以总的时间复杂度是O(nlogn)。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = ;
int a[maxn];
int dp[maxn];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=;i<=n;i++)
        scanf("%d",&a[i]);
    dp[]=a[];
    int len=;
    for(int i=;i<=n;i++)
    {
        if(a[i]>dp[len])
            dp[++len]=a[i];
        else
        {
            int j=std::lower_bound(dp+,dp+len+,a[i])-dp;
            dp[j]=a[i];
        }
    }
    printf("%d\n",len);
    return ;
}

2.　　最长公共子序列

问题描述

给定两个字符串，求解这两个字符串的最长公共子序列（Longest Common Sequence）。比如字符串1：BDCABA；字符串2：ABCBDAB

则这两个字符串的最长公共子序列长度为4，最长公共子序列是：BCBA

解法：c[i,j]表示：(x1,x2....xi) 和 (y1,y2...yj) 的最长公共子序列的长度。

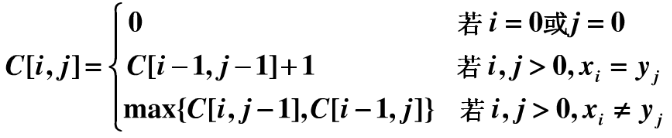
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = ;
char a[maxn],b[maxn];
int dp[maxn][maxn];
int main()
{
    int lena,lenb,i,j;
    while(scanf("%s%s",a,b)!=EOF)
    {
        memset(dp,,sizeof(dp));
        lena=strlen(a);
        lenb=strlen(b);
        for(i=;i<=lena;i++)
        {
            for(j=;j<=lenb;j++)
            {
                if(a[i-]==b[j-])
                {
                    dp[i][j]=dp[i-][j-]+;
                }
                else
                {
                    dp[i][j]=max(dp[i-][j],dp[i][j-]);
                }
            }
        }
        printf("%d\n",dp[lena][lenb]);
    }
    return ;
}

3.　　最长公共子串

比如字符串1：cnblogs；字符串2：belong

则这两个字符串的最长公共子串长度为2，最长公共子串是：lo。

解法：c[i,j]表示：(x1,x2....xi) 和 (y1,y2...yj) 的最长公共子串的长度。

问题描述

给定两个字符串，求解这两个字符串的最长公共子串。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = ;
char a[maxn],b[maxn];
int dp[maxn][maxn];
int main()
{
    int lena,lenb,i,j;
    while(scanf("%s%s",a,b)!=EOF)
    {
        memset(dp,,sizeof(dp));
        lena=strlen(a);
        lenb=strlen(b);
        int ans=-;
        for(i=;i<=lena;i++)
        {
            for(j=;j<=lenb;j++)
            {
                if(i ==  || j == )
                    dp[i][j] = ;
                else if (a[i-] == b[j-])
                {
                    dp[i][j] = dp[i-][j-] + ;
                    ans= max(dp[i][j], ans);
                }
                else
                   dp[i][j] = ;
            }
        }
        printf("%d\n",ans);
    }
    return ;
}            

4.　　01背包

有N件物品和一个容量为V的背包。第i件物品的价格（即体积，下同）是w[i]，价值是c[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

这是最基础的背包问题，总的来说就是：选还是不选，这是个问题<(￣ˇ￣)/

相当于用f[i][j]表示前i个背包装入容量为v的背包中所可以获得的最大价值。

对于一个物品，只有两种情况

　　情况一: 第i件不放进去，这时所得价值为:f[i-1][v]

　　情况二: 第i件放进去，这时所得价值为：f[i-1][v-c[i]]+w[i]

状态转移方程为：f[i][v] = max(f[i-1][v], f[i-1][v-w[i]]+c[i])。

可以优化到一维：

for (int i = ; i <= n; i++)
    for (int j = V; j >= ; j--)
        f[j] = max(f[j], f[j - w[i]] + v[i]);

https://www.luogu.org/problemnew/show/P2925

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <map>
using namespace std;
typedef long long LL;
const int maxn=;
int n,m,k;
int v[maxn];
int dp[maxn];
int main()
{
    scanf("%d %d",&n,&m);
    for(int i=;i<=m;i++)
        scanf("%d",&v[i]);
    for(int i=;i<=m;i++)
    {
        for(int j=n;j>=v[i];j--)
        {
            if(dp[j-v[i]]+v[i]>dp[j])
                dp[j]=dp[j-v[i]]+v[i];
        }
    }
    printf("%d\n",dp[n]);
    return ;
}

5.　　完全背包

有N 种物品和一个容量为V 的背包，每种物品都有无限件可用。第i ii种物品的费用是w[i] ，价值是v[i] 。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

完全背包和01背包十分相像， 区别就是完全背包物品有无限件。由之前的选或者不选转变成了选或者不选，选几件。

和01背包一样，我们可以写出状态转移方程：f[i][v]=max(f[i-1][v-k*c[i]]+k*w[i]|0<=k*c[i]<=v)，看例题：

https://www.luogu.org/problemnew/show/P1853

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <map>
using namespace std;
typedef long long LL;
const int maxn=1e7+;
int s,n,d;
int w[],v[];
int dp[maxn];
int main()
{
    scanf("%d %d %d",&s,&n,&d);
    for(int i=;i<=d;i++)
        scanf("%d %d",&w[i],&v[i]);
    for(int A=;A<=n;A++)
    {
        for(int i=;i<=d;i++)
        {
            for(int j=w[i];j<=s;j++)
                dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
        }
        s+=dp[s];
    }
    printf("%d\n",s);
    return ;
}

6.　　编辑距离

编辑距离的定义是：从字符串A到字符串B，中间需要的最少操作权重。这里的操作权重一般是：

1.删除一个字符(deletion)

2.插入一个字符(insertion)

3.替换一个字符(substitution)

解法：dp[i][j] 表示从 word1 的前i个字符转换到 word2 的前j个字符所需要的步骤。当word1[i] == word2[j]时，dp[i][j] = dp[i - 1][j - 1]，其他情况时，dp[i][j]是其左，左上，上的三个值中的最小值加1，其实这里的左，上，和左上，分别对应的增加，删除，修改操作，转移方程如下：

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        vector<vector<int>> dp(m + , vector<int>(n + ));
        for (int i = ; i <= m; ++i) dp[i][] = i;
        for (int i = ; i <= n; ++i) dp[][i] = i;
        for (int i = ; i <= m; ++i) {
            for (int j = ; j <= n; ++j) {
                if (word1[i - ] == word2[j - ]) {
                    dp[i][j] = dp[i - ][j - ];
                } else {
                    dp[i][j] = min(dp[i - ][j - ], min(dp[i - ][j], dp[i][j - ])) + ;
                }
            }
        }
        return dp[m][n];
    }
};

7.　　两个字符串的最小ASCII删除和

从字符串A到字符串B，每次删除一个字符，求最少ASCII操作权重。

解法思想和上面的差不多，但是问题是要加上那个ASCII 的值，保证这个值最小。

class Solution {
public:
    int minimumDeleteSum(string s1, string s2) {
        int m = s1.size(), n = s2.size();
        vector<vector<int>> dp(m + , vector<int>(n + , ));
        for (int j = ; j <= n; ++j) 
　　　　　　　dp[][j] = dp[][j - ] + s2[j - ];
        for (int i = ; i <= m; ++i)
        {
            dp[i][] = dp[i - ][] + s1[i - ];
            for (int j = ; j <= n; ++j)
            {
                if(s1[i - ] == s2[j - ])
                    dp[i][j] =dp[i - ][j - ]
                else
                    dp[i][j] = min(dp[i - ][j] + s1[i - ], dp[i][j - ] + s2[j - ]);
            }
        }
        return dp[m][n];
    }
};