Linux磁盘和文件系统扩容彻底研究

1.物理卷：

LVM 逻辑卷的底层物理存储单元是一个块设备，比如一个分区或整个磁盘。要在 LVM 逻辑卷中使用该设备，则必须将该设备初始化为物理卷（PV）。

2.卷组：
物理卷合并为卷组（VG）。这样就创建了磁盘空间池，并可使用它分配逻辑卷。

3.逻辑卷：
逻辑卷管理会根据物理存储生成提取层，以便创建逻辑存储卷。这样就比直接使用物理存储在很多方面提供了更大的灵活性。使用逻辑卷时不会受物理磁盘大小限制。另外，软件无法看到硬件存储配置，因此可在不停止应用程序或者卸载文件系统的情况下，重新定义大小并进行移动。这样可降低操作成本。

4.他们三者的关系：
Linux 操作系统中某个文件挂载点对应着逻辑卷。
一个逻辑卷从属一个卷组，可以使用卷组的物理空间。
举例说明：
如果当前系统的root 节点挂载的是 /dev/mapper/centos_-root ,对应的逻辑卷是/dev/centos_/root
逻辑卷大小是10G，那么某天root节点磁盘空间不足了，扩容步骤如下：
a.增加磁盘。
b.对磁盘分区，形成物理卷。
c.将该物理卷加入到/dev/centos_/root 所属的卷组： centos_
d.卷组有了富余空间，那么可以按照需要分配空间给某个逻辑卷/dev/centos_/root

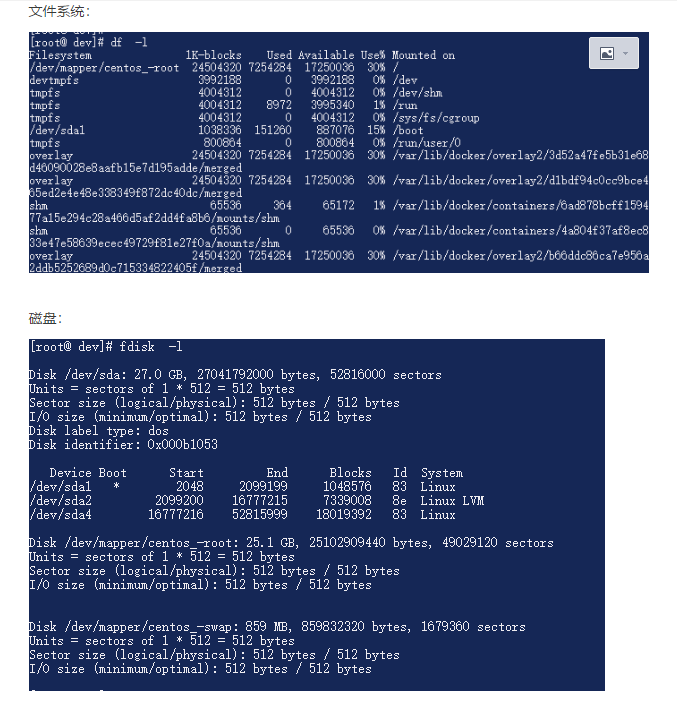
磁盘扩容详细步骤：
http://www.cnblogs.com/wajika/p/6513102.html

逻辑卷物理卷概念：
https://access.redhat.com/documentation/zh-cn/red_hat_enterprise_linux/7/html/logical_volume_manager_administration/logical_volumes