poj2826（细节，计算几何）

题目链接：https://vjudge.net/problem/POJ-2826

题意：平面中摆两根木棍，雨水从上垂直下落，问木棍中能乘多少水。

思路：

　　细节很多，坑QAQ。。

　　首先不相交时肯定为0.00，然后其中有一条木棍是水平的也不行，最后是如果开口被堵住了也不行（通过判断其中一根木棍l1的上端点向上引射线是否与l2相交）。

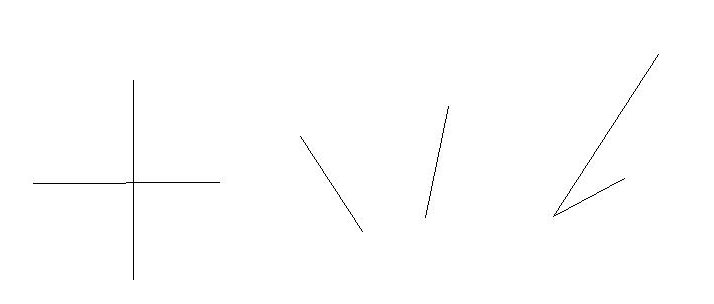
　　最后输出答案时需要加上eps，因为会出现-0.0和0.0的情况，不然会wa到你哭！double的精度就是迷，我也想不通-0.0是怎么出现的，算是经验了，以后碰到输出double的情况注意下-0.0。

AC code：

#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstdlib>
using namespace std;

const double eps=1e-;
const double inf=1e20;

int sgn(double x){
    if(abs(x)<eps) return ;
    if(x<) return -;
    return ;
}

struct Point{
    double x,y;
    Point(){}
    Point(double xx,double yy):x(xx),y(yy){}
    Point operator + (const Point& b)const{
        return Point(x+b.x,y+b.y);
    }
    Point operator - (const Point& b)const{
        return Point(x-b.x,y-b.y);
    }
    double operator * (const Point& b)const{
        return x*b.x+y*b.y;
    }
    double operator ^ (const Point& b)const{
        return x*b.y-b.x*y;
    }
    //绕原点旋转角度b（弧度值），后x、y的变化
    void transXY(double b){
        double tx=x,ty=y;
        x=tx*cos(b)-ty*sin(b);
        y=tx*sin(b)+ty*cos(b);
    }
};

struct Line{
    Point s,e;
    Line(){}
    Line(Point ss,Point ee){
        s=ss,e=ee;
    }
    //两直线相交求交点
    //第一个值为0表示直线重合，为1表示平行，为2表示相交
    //只有第一个值为2时，交点才有意义
    pair<int,Point> operator &(const Line &b)const{
        Point res = s;
        if(sgn((s-e)^(b.s-b.e)) == )
        {
            if(sgn((s-b.e)^(b.s-b.e)) == )
                return make_pair(,res);//重合
            else return make_pair(,res);//平行
        }
        double t = ((s-b.s)^(b.s-b.e))/((s-e)^(b.s-b.e));
        res.x += (e.x-s.x)*t;
        res.y += (e.y-s.y)*t;
        return make_pair(,res);
    }
};
//判断线段相交
bool inter(Line l1,Line l2){
    return
        max(l1.s.x,l1.e.x)>=min(l2.s.x,l2.e.x)&&
        max(l2.s.x,l2.e.x)>=min(l1.s.x,l1.e.x)&&
        max(l1.s.y,l1.e.y)>=min(l2.s.y,l2.e.y)&&
        max(l2.s.y,l2.e.y)>=min(l1.s.y,l1.e.y)&&
        sgn((l1.s-l2.s)^(l2.e-l2.s))*sgn((l1.e-l2.s)^(l2.e-l2.s))<=&&
        sgn((l2.s-l1.s)^(l1.e-l1.s))*sgn((l2.e-l1.s)^(l1.e-l1.s))<=;
}

double dis(Point a,Point b){
    return sqrt((b-a)*(b-a));
}

int T;

int main(){
    scanf("%d",&T);
    double x1,yy1,x2,yy2,x3,yy3,x4,yy4;
    Line l1,l2;
    while(T--){
        scanf("%lf%lf%lf%lf%lf%lf%lf%lf",&x1,&yy1,&x2,&yy2,&x3,&yy3,&x4,&yy4);
        l1=Line(Point(x1,yy1),Point(x2,yy2));
        l2=Line(Point(x3,yy3),Point(x4,yy4));
        if(!inter(l1,l2)){
            printf("0.00\n");
            continue;
        }
        if(sgn(l1.s.y-l1.e.y)==||sgn(l2.s.y-l2.e.y)==){
            printf("0.00\n");
            continue;
        }
        if(sgn(l1.s.y-l1.e.y)<) swap(l1.s,l1.e);
        if(sgn(l2.s.y-l2.e.y)<) swap(l2.s,l2.e);
        if(inter(Line(l1.s,Point(l1.s.x,)),l2)||inter(Line(l2.s,Point(l2.s.x,)),l1)){
            printf("0.00\n");
            continue;
        }
        pair<int,Point> pr=l1&l2;
        Point p=pr.second;
        double ans1,ans2;
        pr=l1&Line(Point(,l2.s.y),l2.s);
        Point p1=pr.second;
        ans1=abs((l2.s-p)^(p1-p))/;
        pr=l2&Line(Point(,l1.s.y),l1.s);
        Point p2=pr.second;
        ans2=abs((l1.s-p)^(p2-p))/;
        printf("%.2f\n",eps+min(ans1,ans2));
    }
    return ;
}