【Python】【demo实验36】【基础实验】【求3*3矩阵的主对角线之和】

题目：

　　求一个3*3矩阵主对角线元素之和。

主对角线：从左上多右下的书归为主对角线

副对角线：从左下至右上的数归为副对角线。

我的源码：

　　

#!/usr/bin/python
# encoding=utf-8
# -*- coding: UTF-8 -*-

# 求一个3*3矩阵主对角线元素之和
# 6  5  8
# 4  1  9
# 7  1  2

l = [[6,5,8],[4,1,9],[7,1,2]]

s = 0
for i in range(len(l)):
    for j in range(len(l)):
        if i == j :
            s = s + l[i][i]
print(s)

那么求副对角线的和：

#!/usr/bin/python
# encoding=utf-8
# -*- coding: UTF-8 -*-

# 求一个3*3矩阵主对角线元素之和
# 6  5  8
# 4  1  9
# 7  1  2

l = [[6,5,8],[4,1,9],[7,1,2]]

s = 0
#print("#",len(l))
for i in range(len(l)):
    for j in range(len(l)):
        if (j == (len(l)-1-i )):
            s = s + l[i][j]
            #print(s)
print(s)

需要注意的是，for循环默认是从0开始的。

原题给出的解答：

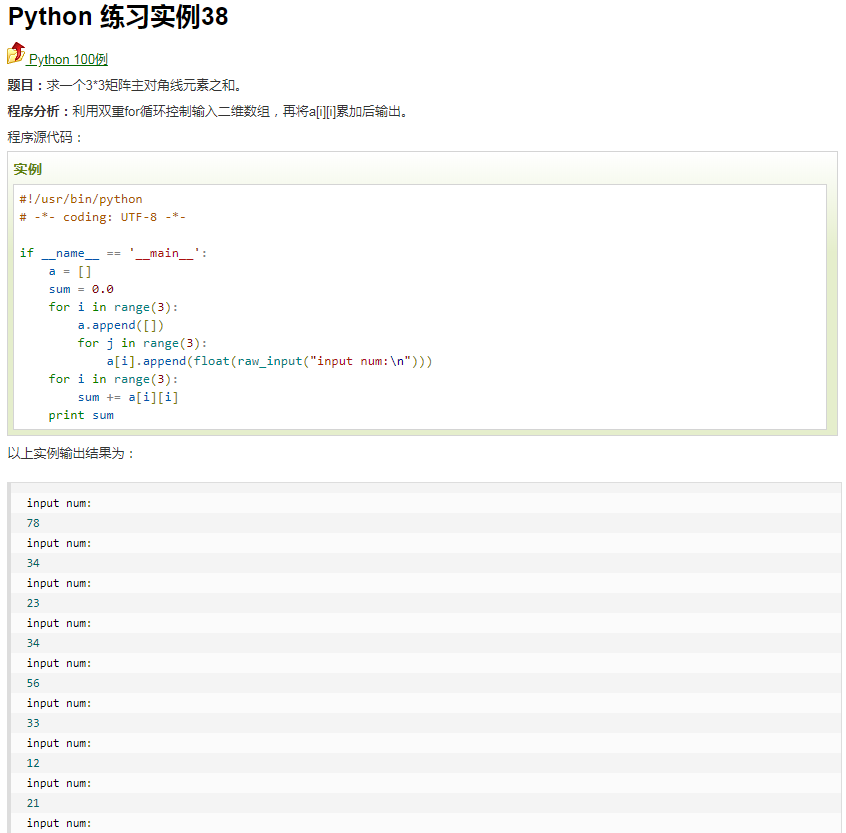
原题，是利用for循环手动输入3*3矩阵的各数字，然后求和的；

————————（我是分割线）————————

参考：

1. RUNOOB.COM：https://www.runoob.com/python/python-exercise-example38.html

备注：

初次编辑时间：2019年10月6日14:10:07

环境：Windows 7   / Python 3.7.2