分布排序（distribution sorts）算法大串讲

ref ： https://dsqiu.iteye.com/blog/1707383

---

 

本文内容框架：

§1 鸽巢排序（Pigeonhole）

§2 桶排序（Bucket Sort）

  §3 基数排序（Radix Sort）

§4 计数排序（Counting Sort）

§5 Proxmap Sort

§6 珠排序(Bead Sort）

§7 小结

本文介绍的排序算法是基于分配、收集的排序算法，分配排序的基本思想：排序过程无须比较关键字，而是通过"分配"和"收集"过程来实现排序.它们的时间复杂度可达到线性阶：O(n)。不受比较排序算法时间复杂度O(nlogn)的下限限制。

§1 鸽巢排序（Pigeonhole）

鸽巢排序(Pigeonhole sort)

鸽巢排序(Pigeonhole sort)，也被称作基数分类, 是一种时间复杂度为O(n)且在不可避免遍历每一个元素并且排序的情况下效率最好的一种排序算法。但它只有在差值(或者可被映射在差值)很小的范围内的数值排序的情况下实用，同时也要求元素个数(n)和成为索引的值(N)大小相当。

鸽巢排序(Pigeonhole sort)算法的时间复杂度都是O(N+n)，空间复杂度是O(N)。

鸽巢排序(Pigeonhole sort)算法的思想就是使用一个辅助数组，这个辅助数组的下标对应要排序数组的元素值即使用辅助数组的下标进行排序，辅助数组元素的值记录该下标元素值的在要排序数组中的个数。

鸽巢排序(Pigeonhole sort)算法步骤：

1.对于给定的一组要排序的数组，需要初始化一个空的辅助数组（“鸽巢”）,把初始数组中的每个值作为一个key(“鸽巢”)即辅助数组的索引即是待排序数组的值。

2.遍历初始数组，根据每个值放入辅助数组对应的“鸽巢”

3.顺序遍历辅助数组，把辅助数组“鸽巢”中不为空的数放回初始数组中

鸽巢排序(Pigeonhole sort)算法实现举例

1. void PigeonholeSort(int *array, int length)
2. {
3. int b[256] = {0};
4. int i,k,j = 0;
5. for(i=0; i<length; i++)
6. b[array[i]]++;
7. for(i=0; i<256; i++)
8. for(k=0; k<b[i]; k++)
9. array[j++] = i;
10. }

其实作者觉得鸽巢排序(Pigeonhole sort)的原理跟哈希表的原理类似——根据关键字的key就可以得到关键字的存储位置。

§2 桶排序（Bucket Sort）

箱排序(Bin Sort)

桶排序 (Bucket sort)或所谓的箱排序，是一个排序算法，工作的原理是将阵列分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递回方式继续使用桶排序进行排序）。桶排序是鸽巢排序的一种归纳结果。当要被排序的阵列内的数值是均匀分配的时候，桶排序使用线性时间（Θ（n））。但桶排序并不是比较排序，不受到 O(n log n) 下限的影响。

1、箱排序的基本思想

　箱排序也称桶排序(Bucket Sort)，其基本思想是：设置若干个箱子，依次扫描待排序的记录R[0]，R[1]，…，R[n-1]，把关键字等于k的记录全都装入到第k个箱子里(分配)，然后按序号依次将各非空的箱子首尾连接起来(收集)。

【例】要将一副混洗的52张扑克牌按点数A<2<…<J<Q<K排序，需设置13个"箱子"，排序时依次将每张牌按点数放入相应的箱子里，然后依次将这些箱子首尾相接，就得到了按点数递增序排列的一副牌。

2、箱排序中，箱子的个数取决于关键字的取值范围。

　若R[0..n-1]中关键字的取值范围是0到m-1的整数，则必须设置m个箱子。因此箱排序要求关键字的类型是有限类型，否则可能要无限个箱子。

3、箱子的类型应设计成链表为宜

　 一般情况下每个箱子中存放多少个关键字相同的记录是无法预料的，故箱子的类型应设计成链表为宜。

4、为保证排序是稳定的，分配过程中装箱及收集过程中的连接必须按先进先出原则进行。

（1） 实现方法一

　每个箱子设为一个链队列。当一记录装入某箱子时，应做人队操作将其插入该箱子尾部；而收集过程则是对箱子做出队操作，依次将出队的记录放到输出序列中。

（2） 实现方法二

　若输入的待排序记录是以链表形式给出时，出队操作可简化为是将整个箱子链表链接到输出链表的尾部。这只需要修改输出链表的尾结点中的指针域，令其指向箱子链表的头，然后修改输出链表的尾指针，令其指向箱子链表的尾即可。

桶排序算法实现举例

1. #include <iostream>
2. #include <list>
3. using namespace std;
4. struct Node
5. {
6. double value;
7. Node *next;
8. };
9. //桶排序主程序
10. void bucketSort(double* arr, int length)
11. {
12. Node key[10];
13. int number = 0;
14. Node *p, *q;//插入节点临时变量
15. int counter = 0;
16. for(int i = 0; i < 10; i++)
17. {
18. key[i].value = 0;
19. key[i].next = NULL;
20. }
21. for(int i = 0; i < length; i++)
22. {
23. Node *insert = new Node();
24. insert->value = arr[i];
25. insert->next = NULL;
26. number = arr[i] * 10;
27. if(key[number].next == NULL)
28. {
29. key[number].next = insert;
30. }
31. else
32. {
33. p = &key[number];
34. q = key[number].next;
35. while((q != NULL) && (q->value <= arr[i]))
36. {
37. q = q->next;
38. p = p->next;
39. }
40. insert->next = q;
41. p->next = insert;
42. }
43. }
44. for(int i = 0; i < 10; i++)
45. {
46. p = key[i].next;
47. if(p == NULL)
48. continue;
49. while(p != NULL)
50. {
51. arr[counter++] = p->value;
52. p = p->next;
53. }
54. }
55. }
56. int main()
57. {
58. double a[] = {0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.12, 0.23, 0.68};
59. bucketSort(a, 10);
60. for(int i = 0; i < 10; i++)
61. {
62. cout << a[i] << " ";
63. }
64. cout << endl;
65. return 0;
66. }

5、算法简析

　分配过程的时间是O(n)；收集过程的时间为O(m) （采用链表来存储输入的待排序记录）或O(m+n)。因此，箱排序的时间为O(m+n)。若箱子个数m的数量级为O(n)，则箱排序的时间是线性的，即O(n)，但最坏情况仍有可能是 O(n ^ 2)。

桶排序只适用于关键字取值范围较小的情况，否则所需箱子的数目 m 太多导致浪费存储空间和计算时间。

桶排序能够扩展为对整数元组序列进行排序，此时按照字典序排序。在面试的海量数据处理题目中，桶排序也很有作用。如对每天数以亿计的数据进行排序，直接排序即使采用nlgn的算法，依然是一件很恐怖的事情，内存也无法容纳如此多的数据。这时桶排序就可以有效地降低数据的数量级，再对降低了数量级的数据进行排序，可以得到比较良好的效果。

§3 基数排序（Radix Sort）

基数排序(Radix Sort)

基数排序(Radix Sort)是对桶排序的改进和推广。唯一的区别是基数排序强调多关键字，而桶排序没有这个概念，换句话说基数排序对每一种关键字都进行桶排序，而桶排序同一个桶内排序可以任意或直接排好序。

1、单关键字和多关键字

　文件中任一记录R[i]的关键字均由d个分量

构成。

若这d个分量中每个分量都是一个独立的关键字，则文件是多关键字的(如扑克牌有两个关键字：点数和花色)；否则文件是单关键字的，

(0≤j<d)只不过是关键字中其中的一位(如字符串、十进制整数等)。

多关键字中的每个关键字的取值范围一般不同。如扑克牌的花色取值只有4种，而点数则有13种。单关键字中的每位一般取值范围相同。

2、基数

　　设单关键字的每个分量的取值范围均是：

C₀≤k_j≤C_rd-1(0≤j<d)

可能的取值个数rd称为基数。

　基数的选择和关键字的分解因关键宇的类型而异:

(1) 若关键字是十进制整数，则按个、十等位进行分解，基数rd=10，C₀=0，C₉=9，d为最长整数的位数；

(2) 若关键字是小写的英文字符串，则rd=26，C_o='a'，C₂₅='z'，d为字符串的最大长度。

3、基数排序的基本思想

　基数排序的基本思想是：从低位到高位依次对Kj(j=d-1，d-2，…，0)进行箱排序。在d趟箱排序中，所需的箱子数就是基数rd，这就是"基数排序"名称的由来。

基数排序的时间复杂度是 O(k·n)，其中n是排序元素个数，k是数字位数。注意这不是说这个时间复杂度一定优于O(n·log(n))，因为k的大小一般会受到 n 的影响。基数排序所需的辅助存储空间为O(n+rd)。

基数排序的方式可以采用LSD（Least significant digital）或MSD（Most significant digital），LSD的排序方式由键值的最右边开始，而MSD则相反，由键值的最左边开始。

基数排序算法实现举例

1. #include <stdio.h>
2. #include <stdlib.h>
3. void radixSort(int[]);
4. int main(void) {
5. int data[10] = {73, 22, 93, 43, 55, 14, 28, 65, 39, 81};
6. printf("\n排序前: ");
7. int i;
8. for(i = 0; i < 10; i++)
9. printf("%d ", data[i]);
10. putchar('\n');
11. radixSort(data);
12. printf("\n排序後: ");
13. for(i = 0; i < 10; i++)
14. printf("%d ", data[i]);
15. return 0;
16. }
17. void radixSort(int data[]) {
18. int temp[10][10] = {0};
19. int order[10] = {0};
20. int n = 1;
21. while(n <= 10) {
22. int i;
23. for(i = 0; i < 10; i++) {
24. int lsd = ((data[i] / n) % 10);
25. temp[lsd][order[lsd]] = data[i];
26. order[lsd]++;
27. }
28. // 重新排列
29. int k = 0;
30. for(i = 0; i < 10; i++) {
31. if(order[i] != 0)  {
32. int j;
33. for(j = 0; j < order[i]; j++, k++) {
34. data[k] = temp[i][j];
35. }
36. }
37. order[i] = 0;
38. }
39. n *= 10;
40. }
41. }

基数排序应用到字符串处理的倍增算法里面，这个倍增算法，要反复的进行排序。如果排序能快一点，这个程序就能快很多。

§4 计数排序（Counting Sort）

计数排序(Counting sort)

计数排序(Counting sort)是一种稳定的排序算法，和基数排序一样都是桶排序的变体。计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值小于等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。

计数排序的原理

设被排序的数组为A,排序后存储到B，C为临时数组。所谓计数，首先是通过一个数组C[i]计算大小等于i的元素个数，此过程只需要一次循环遍历就可以；在此基础上，计算小于或者等于i的元素个数，也是一重循环就完成。下一步是关键：逆序循环，从length[A]到1，将A[i]放到B中第C[A[i]]个位置上。原理是：C[A[i]]表示小于等于a[i]的元素个数，正好是A[i]排序后应该在的位置。而且从length[A]到1逆序循环，可以保证相同元素间的相对顺序不变，这也是计数排序稳定性的体现。在数组A有附件属性的时候，稳定性是非常重要的。

计数排序的前提及适用范围

A中的元素不能大于k,而且元素要作为数组的下标，所以元素应该为非负整数。而且如果A中有很大的元素，不能够分配足够大的空间。所以计数排序有很大局限性，其主要适用于元素个数多，但是普遍不太大而且总小于k的情况，这种情况下使用计数排序可以获得很高的效率。由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。例如：计数排序是用来排序0到100之间的数字的最好的算法，但是它不适合按字母顺序排序人名。但是，计数排序可以用在基数排序中的算法来排序数据范围很大的数组。

当输入的元素是 n 个 0 到 k 之间的整数时，它的运行时间是 Θ(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。

计数排序算法的步骤：

1.找出待排序的数组中最大和最小的元素

2.统计数组中每个值为i的元素出现的次数，存入数组C的第i项

3.对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）

4.反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

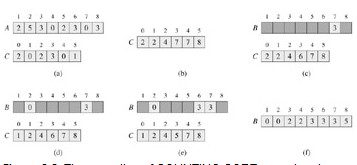
计数排序算法实现举例

1. #include <stdio.h>
2. #include <conio.h>
3. #define MAX 1000
4. //函数原型
5. void counting_sort(int A[],int length_A,int B[],int k);
6. //测试代码
7. int main()
8. {
9. int A[]={-1,2,6,5,4,8,9,7,1,10,3};//1到10,十个测试数据
10. int B[11]={0};
11. int k=10;//所有测试数据都处于0到k之间
12. counting_sort(A,10,B,k);
13. for(int i=1;i<11;i++)
14. printf("%d ",B[i]);
15. getch();
16. }
17. //计数排序
18. void counting_sort(int A[],int length_A,int B[],int k)
19. {
20. int C[MAX]={0};//C是临时数组
21. for(int i=1;i<=length_A;i++)
22. C[A[i]]++;
23. //此时C[i]包含等于i的元素个数
24. for(int i=1;i<=k;i++)
25. C[i]=C[i]+C[i-1];
26. //此时C[i]包含小于或者等于i的元素个数
27. for(int i=length_A;i>=1;i--)//从length_A到1逆序遍历是为了保证相同元素排序后的相对顺序不改变
28. {                           //如果从1到length_A,则相同元素的相对顺序会逆序，但结果也是正确的
29. B[C[A[i]]]=A[i];
30. C[A[i]]--;
31. }
32. }

可以使用链表节省辅助数组C的空间，只存储出现的出现元素情况。

§5 Proxmap Sort

Proxmap Sort

Proxmap Sort是桶排序和基数排序的改进。ProxMap的排序采用不同的方法来排序，这在概念上是类似哈希。该算法使用桶技术对哈希方法进行改变，桶的大小不相同。

Technique:

1. Create 4 arrays and initialize
   1. int HitList[ARRAYSIZE] -- Keeps a count of the number of hits at each index in the sorted array. HitList[x] holds a count of the number of items whose keys hashed to x. Initialize to all 0.
   2. int Location[ARRAYSIZE] -- Indices in the sorted array calculated using the hash function. Item x in the unsorted array has its hash index stored in Location[x]. Does not need to be initialized.
   3. int ProxMap[ARRAYSIZE] -- Starting index in the sorted array for each bucket. If HitList[x] is not 0 then ProxMap[x] contains the starting index for the bucket of keys hashing to x. Initialize to all keys to -1 (unused).
   4. StructType DataArray2[ARRAYSIZE] -- Array to hold the sorted array. Initialize to all -1 (unused).
2. Use the keys of the unsorted array and a carefully chosen hash function to generate the indices into the sorted array and save these. The hash function must compute indices always in ascending order. Store each hash index in the Location[] array. Location[i] will hold the calculated hash index for the i^th structure in the unsorted array. 
   HIdx = Hash(DataArray[i]); 
   Location[i] = HIdx; 

   Care
   must be taken in selecting the hash function so that the keys are
   mapped to the entire range of indexes in the array. A good approach is
   to convert the keys to integer values if they are strings, then map all
   keys to floats in the range 0<= Key < 1. Finally, map these floats
   to the array indices using the following formulas:

       /* Map all integer keys to floats in range 0<= Key < 1 */
       KeyFloat = KeyInt / (1 + MAXKEYINTVALUE);
   
       /* Map all float keys to indices in range 0<= Index < ARRAYSIZE */
       Index = floor(ARRAYSIZE * KeyFloat);
   

   This will then produce indices insuring that all the keys are kept
   in ascending order (hashs computed using a mod operator will not.)

3. Keep a count of the number of hits at each hash index. HitList[Hidx]++
4. Create the ProxMap (short for proximity map) from the hit list giving the starting index in the sorted array for each bucket.

       RunningTotal = 0;        /* Init counter */
       for(i=0; i 0)    /* There were hits at this address */
               {
               ProxMap[i] = RunningTotal;    /* Set start index for this set */
               RunningTotal += HitList[i];
               }
           }
   

5. Move keys from the unsorted array to the sorted array using an insertion sort technique for each bucket. 
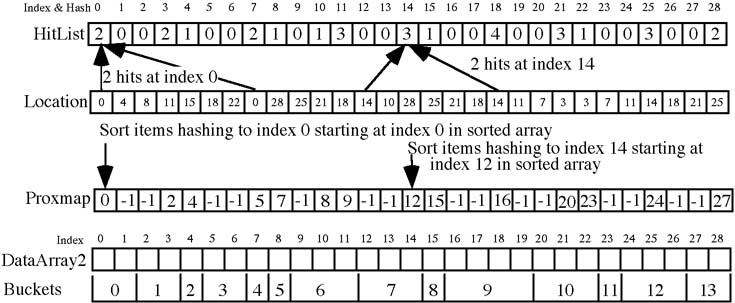
   In this diagram 5 sets of structures are sorted when delta = 5

Analysis: ProxMap sorting runs in a surprisingly fast O(n) time.

1. /******************************************************/
2. /* ProxmapSort.c                                      */
3. /*                                                    */
4. /* Proxmap sort demonstration.                        */
5. /* Author: Rick Coleman                               */
6. /* Date: April 1998                                   */
7. /******************************************************/
8. #include <stdio.h>
9. #include <conio.h>
10. #include "sort.h"
11. #include <math.h>
12. #define ARRAYSIZE    32
13. /* Prototype sort function */
14. void ProxmapSort(StructType DataArray[], StructType DataArray2[],int count);
15. int Hash(int key, int KeyMax, int KeyMin, int count);
16. void ProxMapInsertionSort(StructType DataArray[], StructType *theStruct,
17. int startIdx, int listLen);
18. int main(void)
19. {
20. StructType  DataArray[32], DataArray2[32];
21. int         count;
22. count = ReadRecords(DataArray, 32);
23. printf("Unsorted list of records.\n\n");
24. PrintList(DataArray, count);
25. ProxmapSort(DataArray, DataArray2, count);
26. printf("Sorted list of records.\n\n");
27. PrintList(DataArray2, count);
28. printf("Sorting done...\n");
29. getch();
30. return(0);
31. }
32. /***************************************/
33. /* ProxmapSort()                       */
34. /*                                     */
35. /* Sort records on integer key using   */
36. /*  a proxmap sort.                    */
37. /***************************************/
38. void ProxmapSort(StructType DataArray[], StructType DataArray2[],int count)
39. {
40. int i;
41. int HitList[ARRAYSIZE];
42. int Hidx;                  /* Hashed index */
43. int ProxMap[ARRAYSIZE];
44. int RunningTotal;          /* Number of hits */
45. int Location[ARRAYSIZE];
46. int KeyMax, KeyMin;        /* Used in Hash() */
47. /* Initialize hit list and proxmap */
48. for(i=0; i<count; i++)
49. {
50. HitList[i] = 0;           /* Init to all 0 hits */
51. ProxMap[i] = -1;          /* Init to all unused */
52. DataArray2[i].key = -1;   /* Init to all empty */
53. }
54. /* Find the largest key for use in computing the hash */
55. KeyMax = 0;        /* Guaranteed to be less than the smallest key */
56. KeyMin = 32767;    /* Guaranteed to be more than the largest key */
57. for(i=0; i<count; i++)
58. {
59. if(DataArray[i].key > KeyMax) KeyMax = DataArray[i].key;
60. if(DataArray[i].key < KeyMin) KeyMin = DataArray[i].key;
61. }
62. /* Compute the hit count list (note this is not a collision count, but
63. a collision count+1 */
64. for(i=0; i<count; i++)
65. {
66. Hidx = Hash(DataArray[i].key, KeyMax, KeyMin, count);    /* Calculate hash index */
67. Location[i] = Hidx;                                      /* Save this for later. (Step 1) */
68. HitList[Hidx]++;                                         /* Update the hit count (Step 2) */
69. }
70. /* Create the proxmap from the hit list. (Step 3) */
71. RunningTotal = 0;        /* Init counter */
72. for(i=0; i<count; i++)
73. {
74. if(HitList[i] > 0)    /* There were hits at this address */
75. {
76. ProxMap[i] = RunningTotal;    /* Set start index for this set */
77. RunningTotal += HitList[i];
78. }
79. }
80. // NOTE: UNCOMMENT THE FOLLOWING SECTION TO SEE WHAT IS IN THE ARRAYS, BUT
81. //       COMMENT IT OUT WHEN DOING A TEST RUN AS PRINTING IS VERY SLOW AND
82. //       WILL RESULT IN AN INACCURATE TIME FOR PROXMAP SORT.
83. /* ----------------------------------------------------
84. // Print HitList[] to see what it looks like
85. printf("HitList:\n");
86. for(i=0; i<count; i++)
87. printf("%d ", HitList[i]);
88. printf("\n\n");
89. getch();
90. // Print ProxMap[] to see what it looks like
91. printf("ProxMap:\n");
92. for(i=0; i<count; i++)
93. printf("%d ", ProxMap[i]);
94. printf("\n\n");
95. getch();
96. // Print Location[] to see what it looks like
97. printf("Location:\n");
98. for(i=0; i<count; i++)
99. printf("%d ", Location[i]);
100. printf("\n\n");
101. getch();
102. ---------------------------------------------  */
103. /* Move the keys from A1 to A2 */
104. /* Assumes A2 has been initialized to all empty slots (key = -1)*/
105. for(i=0; i<count; i++)
106. {
107. if((DataArray2[ProxMap[Location[i]]].key == -1))  /* If the location in A2 is empty...*/
108. {
109. /* Move the structure into the sorted array */
110. DataArray2[ProxMap[Location[i]]] = DataArray[i];
111. }
112. else    /* Insert the structure using an insertion sort */
113. {
114. ProxMapInsertionSort(DataArray2, &DataArray[i], ProxMap[Location[i]], HitList[Location[i]]);
115. }
116. }
117. }
118. /***************************************/
119. /* Hash()                               */
120. /*                                     */
121. /* Calculate a hash index.             */
122. /***************************************/
123. int Hash(int key, int KeyMax, int KeyMin, int count)
124. {
125. float    keyFloat;
126. /* Map integer key to float in the range 0 <= key < 1 */
127. keyFloat = (float)(key - KeyMin) / (float)(1 + KeyMax - KeyMin);
128. /* Map float key to indices in range 0 <= index < count */
129. return((int)floor(count * keyFloat));
130. }
131. /***************************************/
132. /* ProxMapInsertionSort()              */
133. /*                                     */
134. /* Use insertion sort to insert a      */
135. /*   struct into a subarray.           */
136. /***************************************/
137. void ProxMapInsertionSort(StructType DataArray[], StructType *theStruct,
138. int startIdx, int listLen)
139. {
140. /* Args:    DataArray - Partly sorted array
141. *theStruct - Structure to insert
142. startIdx - Index of start of subarray
143. listLen - Number of items in the subarray */
144. int i;
145. /* Find the end of the subarray */
146. i = startIdx + listLen - 1;
147. while(DataArray[i-1].key == -1) i--;
148. /* Find the location to insert the key */
149. while((DataArray[i-1].key > theStruct->key) && (i > startIdx))
150. {
151. DataArray[i] = DataArray[i-1];
152. i--;
153. }
154. /* Insert the key */
155. DataArray[i] = *theStruct;
156. }

§6 珠排序(Bead Sort）

珠排序（Bead Sort）

珠排序是一种自然排序算法，由Joshua J.
Arulanandham, Cristian S. Calude 和 Michael J. Dinneen
在2002年发展而来，并且在欧洲理论计算机协会（European Association for Theoretical Computer
Science，简称EATCS）的新闻简报上发表了该算法。无论是电子还是实物(digital and analog
hardware)上的实现，珠排序都能在O(n)时间内完成；然而，该算法在电子上的实现明显比实物要慢很多，并且只能用于对正整数序列进行排序。并且，即使在最好的情况，该算法也需要O(n^2)
的空间。

下面仅从实例来理解这个算法

先了解一个概念,一个数字3用3个1来表示，一个数字9用9个1来表示,珠排序中的珠指的是每一个1,它把每一个1想像成一个珠子,这些珠子被串在一起,想像下算盘和糖葫芦：

图1

上图1中的三个珠就表示数字3,两个珠表示数字2。

图2

图2(a)中有两个数字,4和3,分别串在四条线上,于是数字4的最后一个珠子下落,因为它下边是空的,自由下落后变成图2(b)，图2(c)中随机给了四个数字,分别是3,2,4,2,这些珠子自由下落,就变成了(d)中,落完就有序了,2,2,3,4，以上就是珠排序的精华。

珠排序算法的图很像之前介绍过的跳跃表（Skip List）的结构。

§7 小结

这篇博文列举了选择排序的6个算法，基本可以掌握其中概要，管中窥豹，不求甚解。如果你有任何建议或者批评和补充，请留言指出，不胜感激，更多参考请移步互联网。

参考：

①awsqsh： http://blog.csdn.net/awsqsh/article/details/6133562

②数据结构自考网： http://student.zjzk.cn/course_ware/data_structure/web/paixu/paixu8.6.1.1.htm

③juvenfan：http://www.cnblogs.com/juventus/archive/2012/06/06/2538834.html

④Gossip@caterpillar： http://caterpillar.onlyfun.net/Gossip/AlgorithmGossip/RadixSort.htm

⑤数据结构自考网： http://student.zjzk.cn/course_ware/data_structure/web/paixu/paixu8.6.2.htm

⑥NeilHappy： http://blog.csdn.net/neilhappy/article/details/7202507

⑦kkun： http://www.cnblogs.com/kkun/archive/2011/11/23/2260301.html

⑧Promap Sort： http://www.cs.uah.edu/~rcoleman/CS221/Sorting/ProxMapSort.html