提高组刷题营 DAY 1 下午

DFS

深度优先搜索

通过搜索得到一棵树形图

策略：只要能发现没走过的点，就走到它。有多个点可走就随便挑一个，如果无路可走就回退，再看有没有没走过的点可走。

在图上寻找路径【少数可用最短路解决】：最短路不能解决路径有顺序的，也就是如果路径的边权与之前经过的点火这路有关，那就只能深搜

解决递归形式的问题

有后效性的选择问题

组合问题

状态可能很多，因此数据范围一般较小

1、状态表示

2、剪枝

剪枝的方法：

最优答案剪枝

记忆化剪枝

可行性剪枝

……

1、洪水[ 1s 32M ]

题解

数据范围小，搜索

2、辛苦的老园丁 [1s 128M] [1s 32M]

题解

建反图找团（简单地说，团是G的一个完全子图）

原来输入建图是标记的两点之间不能有连边，建反图之后，连边的就是可以连通的

剪枝：

1.如果一个点与点i当前没有连边，那么之后永远都不会连边，那么就可以把点i从最大团候选中删掉

2.利用可行点剪枝  sum+tot<=ans ，舍弃

3.利用当前答案剪枝ans(2)+tot<=ans

（tot 是团不断累加的权值，sum是序列里面剩下的所有东西的权值和

若sum+tot<=ans ，舍弃）

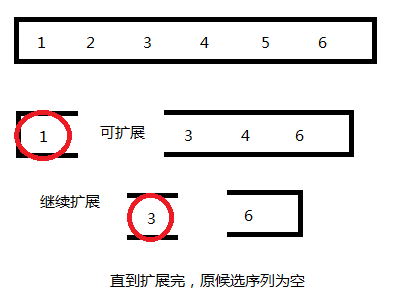
可能组成最大团的点一开始在一个序列里

取出一个点，不断扩展，当序列为空，扩展完了

首先拿出1 ，那么序列被更新为与1相连的点

不断扩展，直到队列为空，找完团了

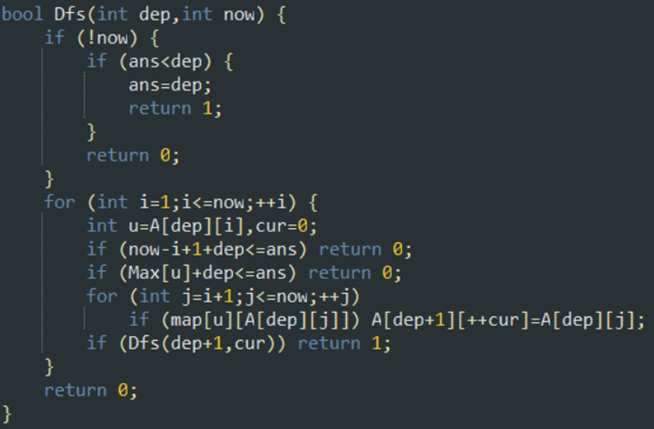
--->sum+tot<=ans

最大团主函数：

为什么找最大团而不是最大独立集呢？？

3、生日蛋糕 [ 1s 10M]

题解

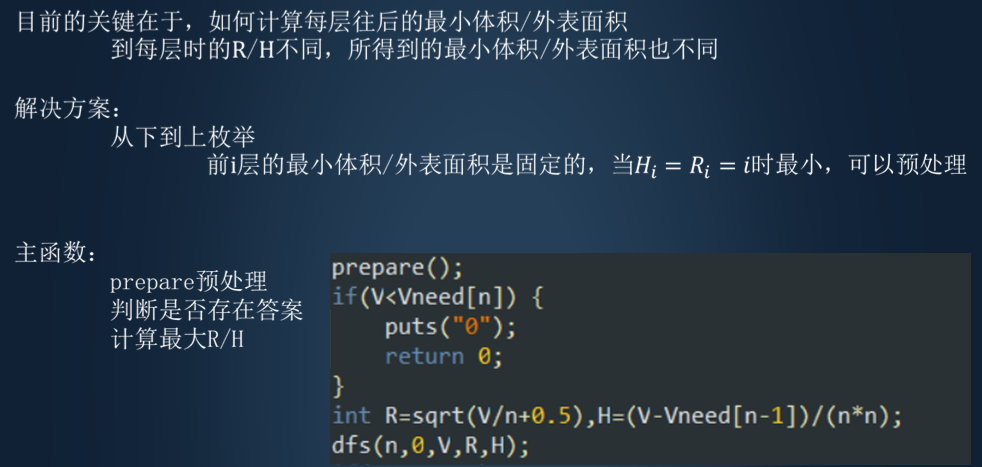
4、靶形数独[2s128M]

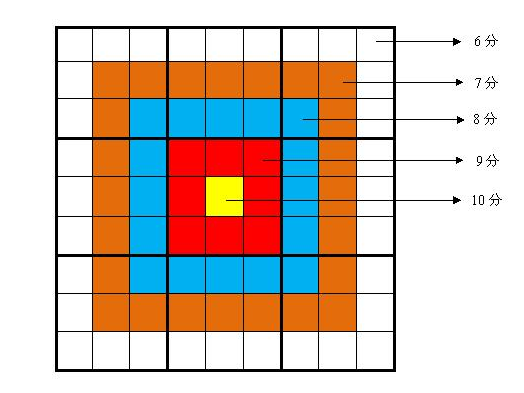
题解

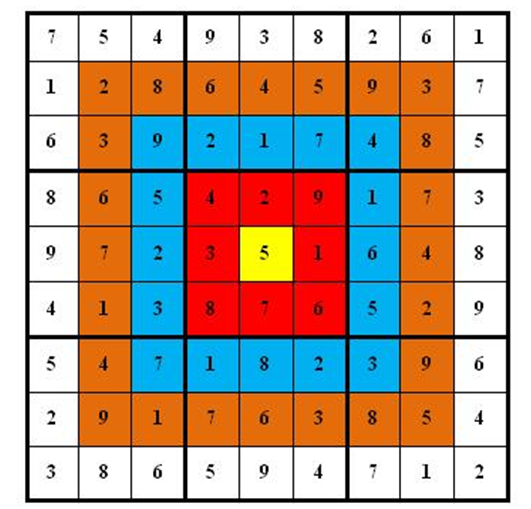
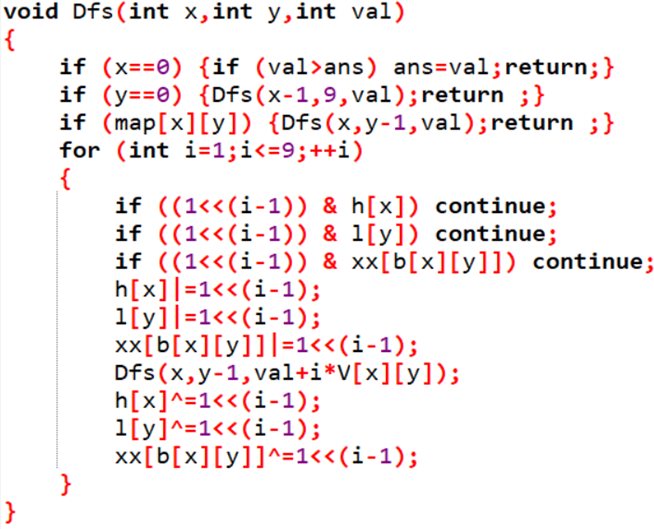
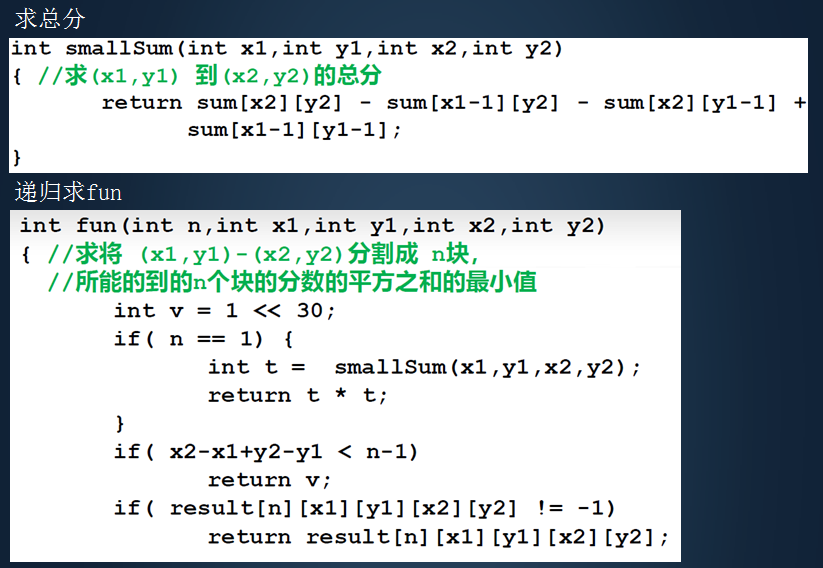
5、棋盘分割 [1s 16M]

题解

---

BFS

宽度优先搜索

1、密室逃脱 [ 1s 64M ]

题解

queue<pair<int,int> > Q;
int FindPath(pair<int,int> b,pair<int,int> e) {
    for (int i=;i<n;++i) for (int j=;j<m;++j) dis[i][j]=1e9+;
    Q.push(b); dis[b.first][b.second]=;
    while (!Q.empty()) {
        pair<int,int> u=Q.front(); Q.pop();
        int x=u.first,y=u.second;
        for (int i=;i<;++i) {
            int tx=x+dx[i],ty=y+dy[i];
            if (CoordValid(tx,ty) && mp[tx][ty]!= && dis[tx][ty]>dis[x][y]+) {
                dis[tx][ty]=dis[x][y]+;
                Q.push(make_pair(tx,ty));
            }
        }
    }
    return dis[e.first][e.second];
}

2、Prime Path[ 1s 64M ]

题解

记录当前素数的值

每次选择一个位置，将其该改为另一个数

检查新的数是否是素数

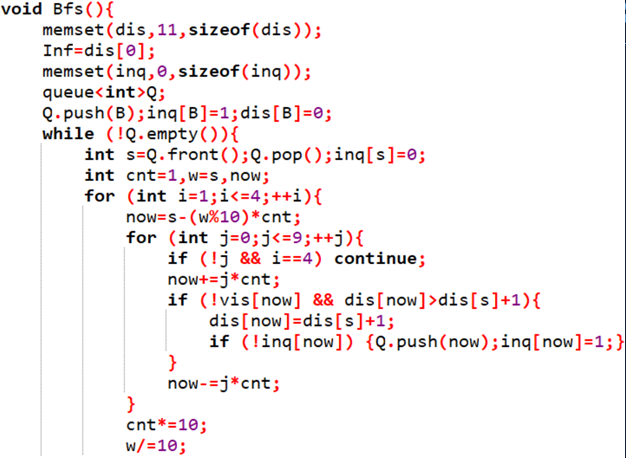
3、拯救行动 [ 1s 64M ]

题解

(Python源码)

BFS部分

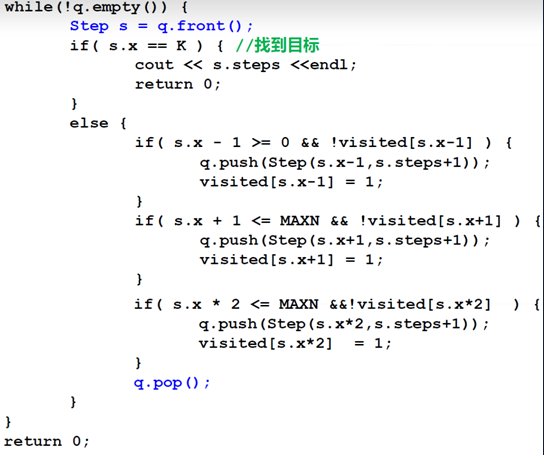
4、抓住那头牛 [ 1s 64M ]

题解

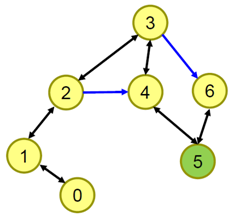
BFS

双向BFS（DBFS）

对比BFS和DFS

广搜一般用于状态表示比较简单求最优策略的问题l

优点：是一种完备策略，即只要问题有解，它就一定可以找到解。并且，广度优先搜索找到的解，还 一定是路径最短的解。

缺点：盲目性较大，尤其是当目标节点距初始节点较远时，将产生许多无用的节点，因此其搜索效率较低。需要保存所有扩展出的状态，占用的空间大

深搜几乎可以用于任何问题

只需要保存 从起始状态到当前状态路径上的节点

根据题目要求凭借自己的经验和对两个搜索的熟练程度做出选择

---

枚举

1、苹果消消乐 [ 1s 64MB]

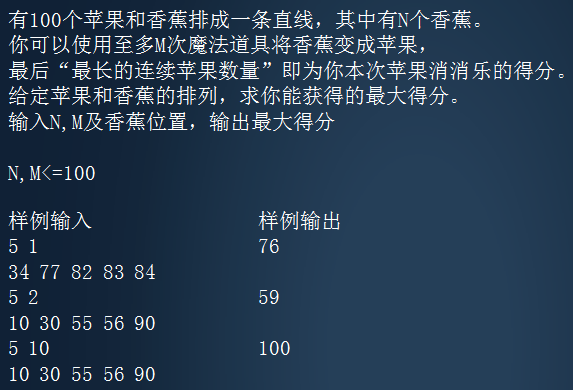
题解

选择连续的香蕉时最优

枚举选择的香蕉起始位置，计算答案

2、Matrix  [ 2s  512MB ]

题解

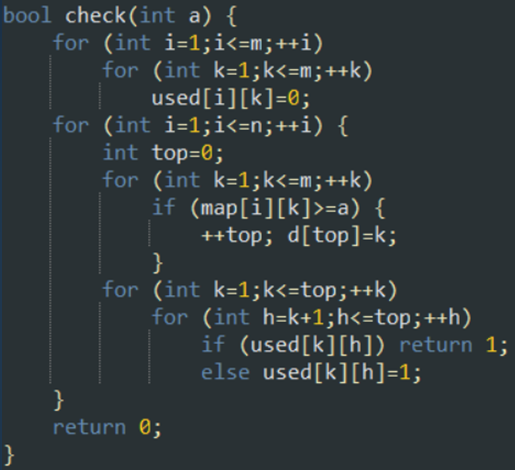
Check函数：

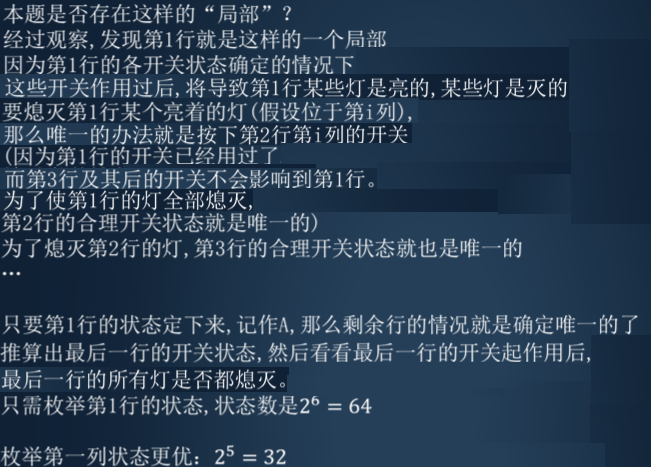
4、特殊密码锁[ 1s 64M ]

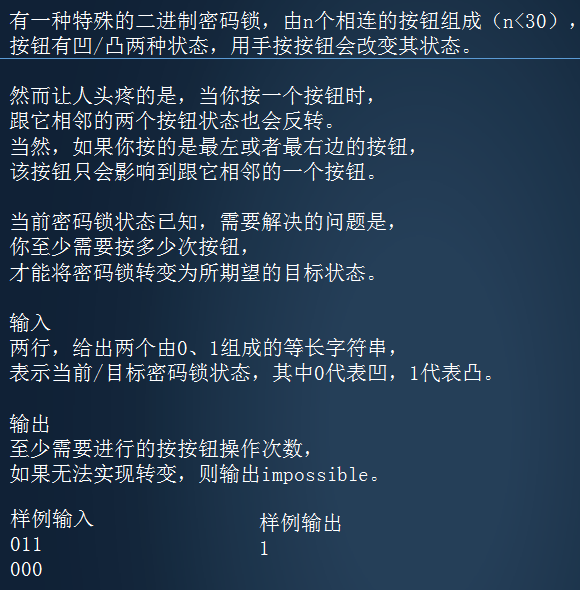
题解

1、  已知，在首位状态固定后，后续的操作是确定的。

2、  只需要枚举首位是否按即可。

5、恼人的青蛙[ 2s 64M ]

题解

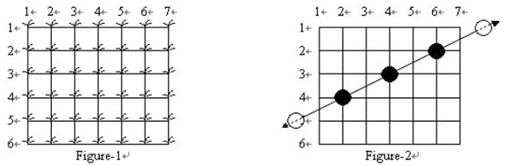
①不是一条行走路径：只有两棵被踩踏的水稻；

②是一条行走路径，但不包括（2，6）上的水道；

③不是一条行走路径：虽然有3棵被踩踏的水稻，

但这三棵水稻之间的距离间隔不相等。

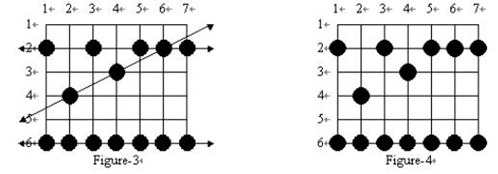
例如，图4的答案是7，

因为第6行上全部水稻恰好构成一条青蛙行走路径。

题解

枚举主函数

枚举得到最大步数

重识枚举

枚举：基于已知信息的猜测,从可能的答案集合中枚举并验证

验证复杂度尽可能小

枚举范围尽可能小（利用条件缩小枚举空间）

选择合理的枚举顺序（正序，倒序）

枚举什么？

怎么枚举？

怎么减少枚举？

---

二进制枚举

5、熄灯问题[ 1s 64M ]

题解

二进制枚举

推导最后一行

二进制枚举

二进制的枚举一般用以枚举集合

对集合的枚举涉及到不同的集合内部元素的选择

枚举子集

for(int S1=S;S1!=0;S1=(S1-1)&S){

S2=S^S1;

}