HDU 6088 - Rikka with Rock-paper-scissors | 2017 Multi-University Training Contest 5

思路和任意模数FFT模板都来自 这里

看了一晚上那篇《再探快速傅里叶变换》还是懵得不行，可能水平还没到- -

只能先存个模板了，这题单模数NTT跑了5.9s，没敢写三模数NTT，可能姿势太差了...

具体推导大概这样就可以了：

/*
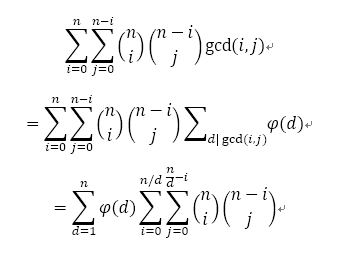
HDU 6088 - Rikka with Rock-paper-scissors [ 任意模数FFT,数论 ]  |  2017 Multi-University Training Contest 5
题意：
	计算 3^n * ∑ [0<=i+j<=n] C(n, i) * C(n-i, j) * GCD(i,j)
	N <= 1e5
分析：
	利用 n = ∑ [d|n] φ(d)
	化得：
		3^n * ∑[1<=d<=n] d ∑ [0<=i+j<=n/d] C(n,i*d) * C(n-i*d, j*d)
	之后枚举 d  （以下略写 *d ）
		C(n,i*d) * C(n-i*d, j*d)
		= n! * 1/(i!) * 1/(j!) * 1/(n-i-j)!
			维护 f(i) = 1/i! 的卷积 g(k) = ∑ [i+j == k] * f(i) * f(j)
		原式 = ∑[1<=i<=m] n! * g(k) * 1/(n-k)!
	由于 gcd(0, 0) == 0
	所以特判卷积的 g(0) 项不用加上
*/
#include <bits/stdc++.h>
using namespace std;
#define MOD mod
#define upmo(a,b) (((a)=((a)+(b))%MOD)<0?(a)+=MOD:(a))
typedef long long LL;
typedef double db;
const int N = 1e5+5;
int t, n;
LL inv[N], F[N], Finv[N], phi[N];
LL MOD;
namespace FFT_MO
{
    const int FFT_MAXN = 1<<18;
    const db PI = 4*atan(1.0);
    struct cp
    {
        db a, b;
        cp(db a_ = 0, db b_ = 0) {
            a = a_, b = b_;
        }
        cp operator + (const cp& rhs) const {
            return cp(a+rhs.a, b+rhs.b);
        }
        cp operator - (const cp& rhs) const {
            return cp(a-rhs.a, b-rhs.b);
        }
        cp operator * (const cp& rhs) const {
            return cp(a*rhs.a-b*rhs.b, a*rhs.b + b*rhs.a);
        }
        cp operator !() const{
            return cp(a, -b);
        }
    }nw[FFT_MAXN+1], f[FFT_MAXN], g[FFT_MAXN], t[FFT_MAXN];
    int bitrev[FFT_MAXN];
    void fft_init()
    {
        int L = 0; while ((1<<L) != FFT_MAXN) L++;
        for (int i = 1; i < FFT_MAXN; i++)
            bitrev[i] = bitrev[i>>1]>>1 | ((i&1)<<(L-1));
        for (int i = 0; i <= FFT_MAXN; i++)
            nw[i] = cp((db)cosl(2*PI/FFT_MAXN*i), (db)sinl(2*PI/FFT_MAXN*i));
    }
    void dft(cp *a, int n, int flag = 1)
    {
        int d = 0; while ((1<<d)*n != FFT_MAXN) d++;
        for (int i = 0; i < n; i++) if (i < (bitrev[i]>>d))
            swap(a[i], a[bitrev[i]>>d]);
        for (int l = 2; l <= n; l <<= 1)
        {
            int del = FFT_MAXN/l*flag;
            for (int i = 0; i < n; i += l)
            {
                cp *le = a+i, *ri = a+i+(l>>1);
                cp *w = flag==1 ? nw : nw+FFT_MAXN;
                for (int k = 0; k < (l>>1); k++)
                {
                    cp ne = *ri * *w;
                    *ri = *le - ne, *le = *le+ne;
                    le++, ri++, w += del;
                }
            }
        }
        if (flag != 1) for (int i = 0; i < n; i++) a[i].a /= n, a[i].b /= n;
    }
    void convo(LL *a, int n, LL *b, int m, LL *c)
    {
        for (int i = 0; i <= n+m; i++) c[i] = 0;
        int N = 2; while (N <= n+m) N <<= 1;
        for (int i = 0; i < N; i++)
        {
            LL aa = i <= n ? a[i] : 0, bb = i <= m ? b[i] : 0;
            aa %= MOD, bb %= MOD;
            f[i] = cp(db(aa>>15), db(aa&32767));
            g[i] = cp(db(bb>>15), db(bb&32767));
        }
        dft(f, N), dft(g, N);
        for (int i = 0; i < N; i++)
        {
            int j = i ? N-i : 0;
            t[i] = ((f[i]+!f[j])*(!g[j]-g[i]) + (!f[j]-f[i])*(g[i]+!g[j])) * cp(0, 0.25);
        }
        dft(t, N, -1);
        for (int i = 0; i <= n+m; i++) upmo(c[i], (LL(t[i].a+0.5))%MOD<<15);
        for (int i = 0; i < N; i++)
        {
            int j = i? N-i : 0;
            t[i] = (!f[j]-f[i])*(!g[j]-g[i])*cp(-0.25,0) + cp(0,0.25)*(f[i]+!f[j])*(g[i]+!g[j]);
        }
        dft(t, N, -1);
        for (int i = 0; i <= n+m; i++)
            upmo(c[i], LL(t[i].a+0.5)+(LL(t[i].b+0.5)%MOD<<30));
    }
}
LL a[1<<18|1], b[1<<18|1], c[1<<18|1];
LL PowMod(LL a, LL m)
{
    a %= MOD;
    LL ret = 1;
    while (m) {
        if (m&1) ret = ret * a % MOD;
        m >>= 1;
        a = a*a % MOD;
    }
    return ret;
}
void GetEuler()
{
    memset(phi, 0, sizeof(phi));
    phi[1] = 1;
    for (int i = 2; i < N; i++)
        if (!phi[i])
            for (int j = i; j < N; j += i)
            {
                if (!phi[j]) phi[j] = j;
                phi[j] = phi[j] / i * (i-1);
            }
}
void init(int n) {
    inv[1] = 1;
    for (int i = 2; i <= n; i++)
        inv[i] = (MOD - MOD/i) *inv[MOD % i] % MOD;
    F[0] = Finv[0] = 1;
    for (int i = 1; i <= n; i++) {
        F[i] = F[i-1] * i % MOD;
        Finv[i] = Finv[i-1] * inv[i] % MOD;
    }
}
int main()
{
    GetEuler();
    scanf("%d", &t);
    while (t--)
    {
        scanf("%d%lld", &n, &MOD);
        init(n);
        FFT_MO::fft_init();
        LL ans = 0;
        for (int d = 1; d <= n; d++)
        {
            int m = n/d;
            for (int i = 0; i <= m; i++) b[i] = a[i] = Finv[i*d];
            FFT_MO::convo(a, m, b, m, c);
            for (int i = 0; i <= m; i++) c[i] = c[i] * Finv[n-i*d] % MOD;
            LL sum = 0;
            for (int i = 1; i <= m; i++) sum = (sum + c[i]) % MOD;
            ans = (ans + sum * phi[d]) % MOD;
        }
        ans = ans * F[n] % MOD * PowMod(3, n) % MOD;
        printf("%lld\n", ans);
    }
}