51nod1040 最大公约数之和，欧拉函数或积性函数

1040 最大公约数之和

　　给出一个n，求1-n这n个数，同n的最大公约数的和。比如：n = 6时，1,2,3,4,5,6 同6的最大公约数分别为1,2,3,2,1,6，加在一起 = 15

　　看起来很简单对吧，但是n<=1e9，所以暴力是不行的，所以要把公式进行推导。

　　引用51nod1040最大公约数之和（欧拉函数）

　　

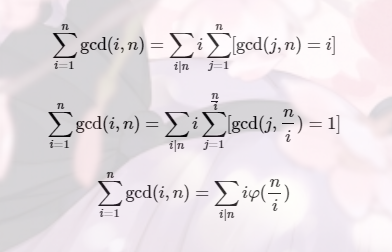
　　这个自己上手推一下也很好推的，不过没推过公式的可能不太懂。

 #include<cstdio>
 #include<cmath>
 typedef long long ll;
 const int N=;
 bool nop[N]={false};
 int pn,pri[N];
 void init()
 {
     pn=;
     for(int i=;i<N;i++)
     {
         if(!nop[i])
             pri[pn++]=i;
         for(int j=;j<pn&&1ll*i*pri[j]<N;j++)
         {
             nop[i*pri[j]]=true;
             if(i%pri[j]==)
                 break;
         }
     }
 }
 int phi(int x)
 {
     int ans=x;
     for(int i=;i<pn&&pri[i]*pri[i]<=x;i++)
         if(x%pri[i]==)
         {
             ans=ans-ans/pri[i];
             while(x%pri[i]==)
                 x/=pri[i];
         }
     if(x>)
         ans=ans-ans/x;
     return ans;
 }
 ll solve(int x)
 {
     ll ans=;
     int xx=sqrt(x);
     for(int i=;i<=xx;i++)
     {
         if(x%i==)
         {
             ans+=i*phi(x/i);
             if(x/i!=i)
                 ans+=x/i*phi(i);
         }
     }
     return ans;
 }
 int main()
 {
     int n;
     init();
     while(~scanf("%d",&n))
         printf("%lld\n",solve(n));
     return ;
 }

欧拉函数

　　另一个方法就是首先可以观察看出f（n）=∑gcd(i,n)是积性函数的性质（不懂证明），然后借用积性函数的性质

　　

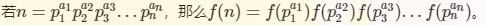
　　这样要求f(n)，我们只需要知道f(p^k)等于多少就行了，而f(p^k)的话

　　

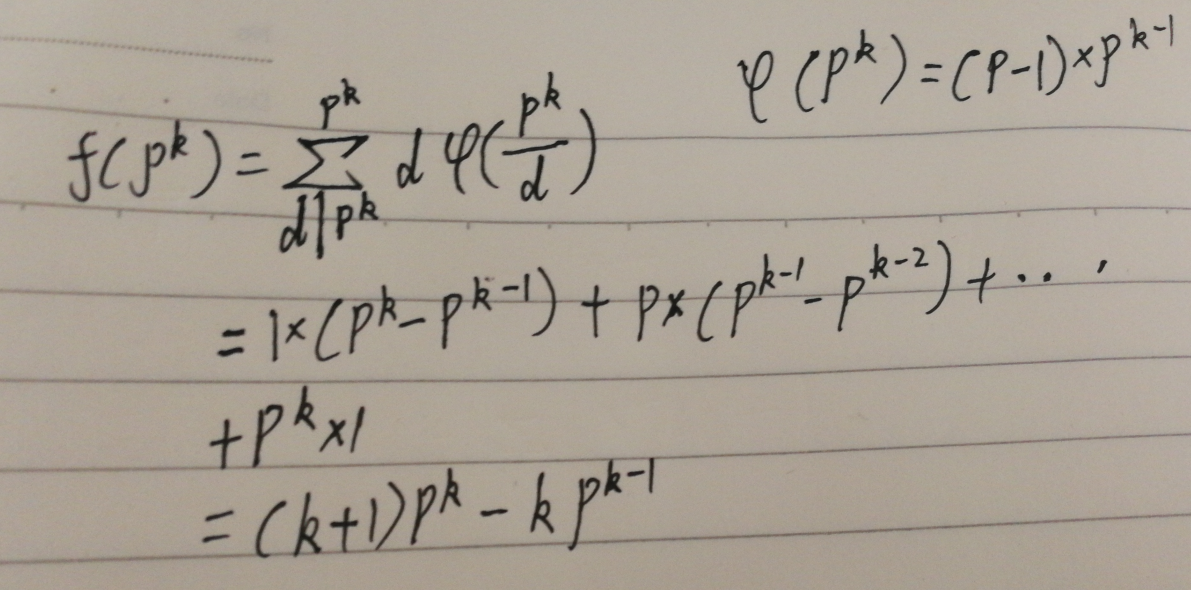
　　而不懂怎么化简成最后一步的话，直接跑第一步的式子也行，因为p^k它的因子也不会有多少个

 #include<cstdio>
 #include<cmath>
 typedef long long ll;
 const int N=;
 bool nop[N]={false};
 int pn,pri[N];
 void init()
 {
     pn=;
     for(int i=;i<N;i++)
     {
         if(!nop[i])
             pri[pn++]=i;
         for(int j=;j<pn&&1ll*i*pri[j]<N;j++)
         {
             nop[i*pri[j]]=true;
             if(i%pri[j]==)
                 break;
         }
     }
 }
 int phi(int x)
 {
     int ans=x;
     for(int i=;i<pn&&pri[i]*pri[i]<=x;i++)
         if(x%pri[i]==)
         {
             ans=ans-ans/pri[i];
             while(x%pri[i]==)
                 x/=pri[i];
         }
     if(x>)
         ans=ans-ans/x;
     return ans;
 }
 //不化简
 //ll solve(int x)
 //{
 //    ll ans=1,res;
 //    for(int i=0;i<pn&&pri[i]<=x;i++)
 //    {
 //        if(x%pri[i]==0)
 //        {
 //            int y=1,z,num=0;
 //            res=0;
 //            while(x%pri[i]==0)
 //            {
 //                x/=pri[i];
 //                y*=pri[i];
 //            }
 //            z=y;
 //            while(z)
 //            {
 //                res+=1ll*(y/z-num)*z;
 //                num=y/z;
 //                z/=pri[i];
 //            }
 //            ans*=res;
 //        }
 //    }
 //    if(x>1)
 //        ans*=2ll*x-1;
 //    return ans;
 //}
 ll solve(int x)
 {
     ll ans=;
     int xx=sqrt(x);
     for(int i=;i<=xx;i++)
     {
         if(x%i==)
         {
             ans+=i*phi(x/i);
             if(x/i!=i)
                 ans+=x/i*phi(i);
         }
     }
     return ans;
 }
 int main()
 {
     int n;
     init();
     while(~scanf("%d",&n))
         printf("%lld\n",solve(n));
     return ;
 }

自己瞎搞