【IOI2018】机械娃娃

看到的时候感到很不可做，因为所有的开关都要状态归零。因此可以得到两分的好成绩。

……然后 yhx-12243 说：这不是线段树优化建图吗？

于是我获得了启发，会做了……

还不是和上次一样，通过提示做出这种交互题的？

我还是太菜了

以下魔改自我的思考过程（一开始想对每一个触发器配一组开关决策下一步，然后听说用线段树直接想到一组开关决策整颗树了）

其实前半部分的思考貌似没用，直接套到整棵树上是适用的

---

因为状态要清零，考虑清空这个状态。

考虑每个触发器连向一个开关，来决策下一步走什么，因为和二进制有关，所以我们构造一个线段树类似的。

假设出现 \(s\) 次，记 \(L = 2^k \geq s\) 使得 \(k\) 最小。

那么我们前 \(L - s\) 次就开个到根的边，后面 \(s\) 次就可以直接走后继了。

那么如果走了 \(L\) 步，线段树内所有点都遍历到了。

注意到 \(L\) 是二的幂，跑完后所有非叶节点区间长度都是偶数，即遍历到偶数次，即清零了。这也说明了为什么不用普通线段树。

所以要把叶子结点全部扔掉，不然就会有节点只遍历到一次。如果扔掉叶子，那么就是一棵大小为 \(L - 1\) 的树。

注意特判一下最后一个点的后继是 \(0\)。

这样点数是 \(2n\) 的 （对于一个 \(s\)，有 \(s \leq L < 2s\)），可以获得 \(50\) 分。

考虑优化这个，发现很多的点是没有用的，即整个区间都会再次回到根。那么要访问到这个区间的时候，不如提前回到根。即删掉这个点，父亲连向自己的边改为连向根。

但是发现优化力度不大，这是因为这道题的遍历方式使得遍历的点交错了起来。

因为最后一个点是在右边的，那么我们把线段树右边的那 \(s\) 个点取来，钦定它们是出边，然后根据先前遍历的顺序把值钦定一下就好。

我们只选了右边的点，优化力度很明显了。

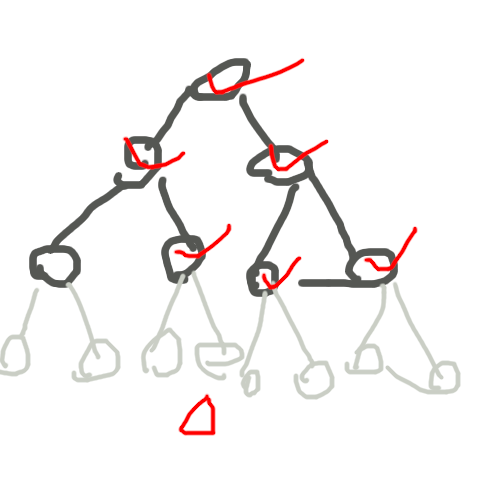
对于 \(s = 5\), \(L = 8\)，淡色是叶子，打钩的是有用的点。（机房没带数位板请见谅，其他软件不会用，求dalao推荐）

可以证明对于一个 \(N\) ，点数是 \(N - 1 + \lceil \log_2 N \rceil\)。考虑对于相同的 \(L\)， 考虑 \(N\) 个叶子，至少要 \(N - 1\) 个点，而多出来的是单独一条链，也就是最后一个元素向上的链。这个链长度小于等于 \(\lceil \log_2 N \rceil\)。

所以这样子就能得到较为优秀的分数了。

然而对于每一个触发器，我们都会多一个 \(\log\)。那么为什么不放在一起呢？这样正好符合正解的复杂度。

考虑用一个统一的开关线段树维护这些触发器，然后触发器回到决策线段树的开头。

注意触发器不能回到起点，因为一个触发器可能出现多次，那么我们很难决定它是最后一个的时候怎么做。

为了回到起点，我们增加一个虚点，或者换句话说，就是往规定的触发器序列末尾加一个 \(0\)。

和上面的方法类似，我们把叶子的遍历序列存下来，同时只取在线段树右边的 \(N + 1\) 个点，根据遍历的时间来钦定触发器。

一样的，因为遍历了二的幂次，所以所有开关归零，经过开关次数 \(O\left(N \log N\right)\) 大概 \(3 \times 10^6\)，也不会爆炸。

开关个数 \(O\left(N + \lceil \log_2 \left(N + 1\right) \rceil\right)\)，因为judger对这个 \(\log\) 的界卡的不紧，大概可以大 \(1\)，所以刚好能通过此题。

看到有些人用bitreverse，的确这样子就是bitreverse后的不断+1，可以给各种操作带来方便。

#include "doll.h"
#include <bits/stdc++.h>
typedef std::vector<int> VI;
const int MAXN = 262145;
const int spe = 19260817;
int idx[MAXN], xs[MAXN], ys[MAXN];
int qli[MAXN];
int typ[MAXN], cnto[MAXN], tot, lim, N;
int tli[MAXN], t0t, cnt[MAXN];
void qry(int u, int l, int r) {
	if (l == r) {
		cnto[l] = ++tot;
		return ;
	}
	int mid = l + r >> 1;
	!typ[u] ? qry(u << 1, l, mid) : qry(u << 1 | 1, mid + 1, r);
	typ[u] ^= 1;
}
void relable(int u, int l, int r) {
	if (l == r) {
		tli[++t0t] = l;
		return ;
	}
	int mid = l + r >> 1;
	relable(u << 1 | 1, mid + 1, r);
	relable(u << 1, l, mid);
}
int txt;
int build(int l, int r) {
	if (l == r) {
		int now = cnt[l];
		return now > 0 ? qli[now] : spe;
	}
	int mid = l + r >> 1;
	int tl = build(l, mid), tr = build(mid + 1, r);
	if (tl == spe && tr == spe) return spe;
	int now = ++txt;
	xs[now] = tl, ys[now] = tr;
	return -now;
}
void create_circuit(int M, VI A) {
	N = A.size(); ++N;
	lim = 1;
	while (lim < N) lim <<= 1;
	for (int i = 1; i <= lim; ++i) qry(1, 1, lim);
	relable(1, 1, lim);
	std::sort(tli + 1, tli + 1 + N, [] (int a, int b) { return cnto[a] < cnto[b]; });
	for (int i = 1; i <= N; ++i)
		cnt[tli[i]] = i;
	std::copy(A.begin(), A.end(), qli + 1);
	VI C(M + 1, 0), X, Y;
	int rt = build(1, lim);
	for (int i = 1; i <= txt; ++i) {
		xs[i] == spe ? xs[i] = rt : 0;
		ys[i] == spe ? ys[i] = rt : 0;
	}
	for (int i = 0; i <= M; ++i) C[i] = rt;
	X.assign(xs + 1, xs + 1 + txt);
	Y.assign(ys + 1, ys + 1 + txt);
	answer(C, X, Y);
}