（数据科学学习手札12）K-means聚类实战（基于R）

上一篇我们详细介绍了普通的K-means聚类法在Python和R中各自的实现方法，本篇便以实际工作中遇到的数据集为例进行实战说明。

数据说明：

本次实战样本数据集来自浪潮集团提供的美团的商家信息，因涉及知识产权问题恕难以提供数据地址；

我选择的三个维度的数值型数据分别为“商家评分”，“商家评论数”，“本月销售额”，因为数值极差较大，故对原数据先进行去缺省值-标准化处理，再转为矩阵形式输入K-means算法之中，经Rtsne对原数据进行降维后具体代码和可视化聚类效果如下：

rm(list=ls())
library(readxl)
library(Rtsne)
setwd('C:\\Users\\windows\\Desktop')
data <- read_xlsx('重庆美团商家信息.xlsx')
token <- data[1,1]
data <- subset(data,数据所属期 == token,select=c('商家评分','商家评论数','本月销售额'))
input <- as.matrix(na.omit(data))
#数据标准化
input <- scale(as.matrix(input))
#数据降维
tsne <- Rtsne(input,check_duplicates = FALSE)

#自定义代价函数计算函数
Mycost <- function(data,centers_){
  l <- length(data[,1])
  d <- matrix(0,nrow=l,ncol=length(centers_[,1]))
  for(i in 1:l){
    for(j in 1:length(centers_[,1])){
      dd <- 0
      for(k in 1:length(data[1,])){
        dd <- dd + (data[i,k]-centers_[j,k])^2
      }
      d[i,j] <- sqrt(dd)
    }
  }
  mindist <- apply(d,1,min)
  return(sum(mindist))
}
colors = c('red','green','yellow','black','blue','grey')
#对k的值进行试探
cost <- c()
par(mfrow=c(2,3))
for(k in 2:7){
  cl <- kmeans(input,centers=k)
  plot(tsne$Y,col=colors[cl$cluster],iter.max=50)
  title(paste(paste('K-means Cluster of ',as.character(k),'Clusters')))
  cost[k-1] <- Mycost(input,cl$centers)
}
#绘制代价函数变化情况
par(mfrow=c(1,1))
plot(2:7,cost,type='o',xlab='K',ylab='Cost')
title('Cost Change')

代价函数变化情况如下：

根据上述代价函数变化情况，依据肘部法则，选取k=3，下面得到k取定3时具体的聚类结果：

cl <- kmeans(input,centers=3,iter.max=50)
plot(tsne$Y,col=colors[cl$cluster])
title(paste(paste('K-means Cluster of ',as.character(3),'Clusters')))

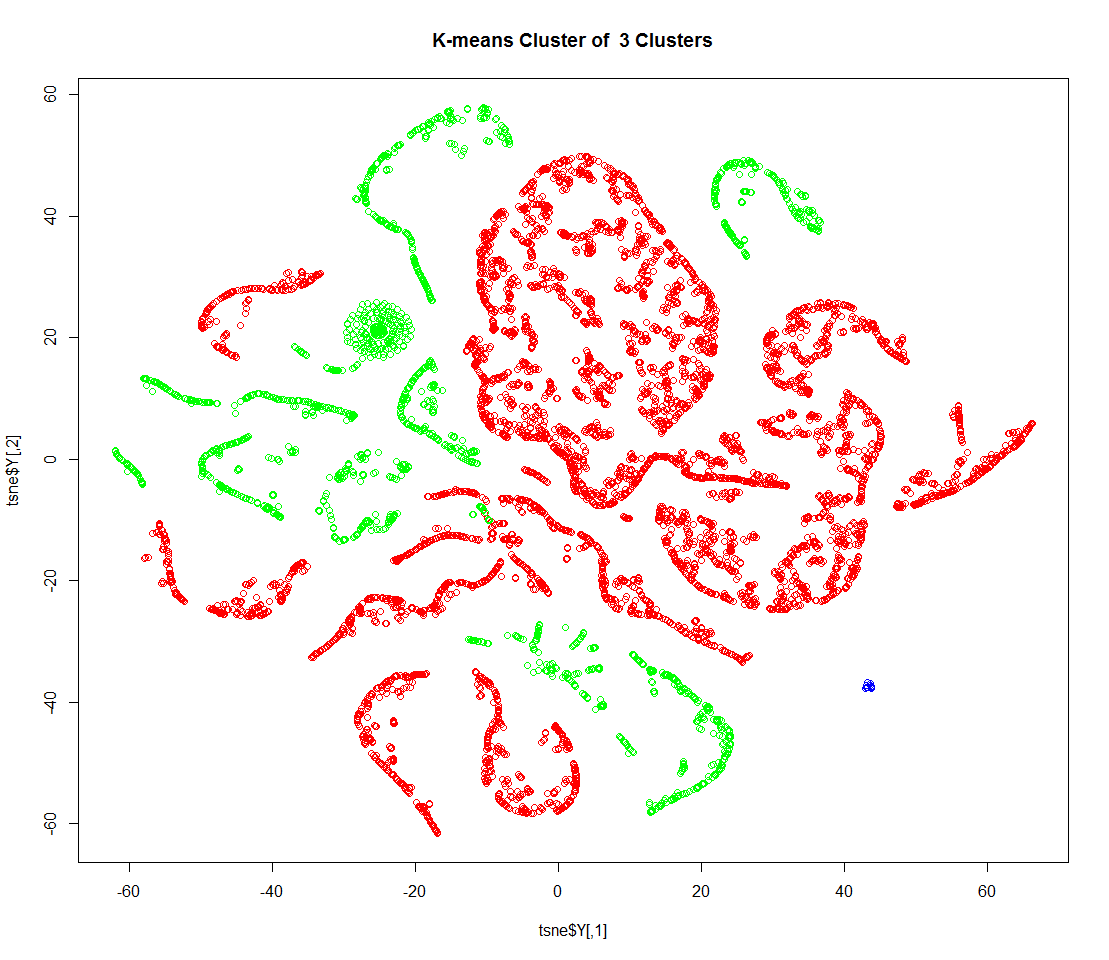
再根据聚类的标号结果，进行下面一系列具体的分析：

先来看这三类的平均销售额：

anl <- na.omit(data)
anl$类别 <- cl$cluster
str(anl)

type1 <- subset(anl,类别==1)

type2 <- subset(anl,类别==2)

type3 <- subset(anl,类别==3)

goaldata <- matrix(0,nrow=3,ncol=3)
goaldata[1,] = apply(type1[,1:3],2,mean)
goaldata[2,] = apply(type2[,1:3],2,mean)
goaldata[3,] = apply(type3[,1:3],2,mean)

barplot(log(t(goaldata[3,])),names.arg = c('Type1','Type2','Type3'),xlab='Type',ylab='对数化数值')
title('销售额')

店铺平均评分：

店铺平均评论数：

下面再绘制出这三种type的各指标密度分布：

par(mfrow=c(1,3))
plot(density(type1$商家评分))
plot(density(type1$商家评论数))
plot(density(type1$本月销售额))

par(mfrow=c(1,3))
plot(density(type2$商家评分))
plot(density(type2$商家评论数))
plot(density(type2$本月销售额))

par(mfrow=c(1,3))
plot(density(type3$商家评分))
plot(density(type3$商家评论数))
plot(density(type3$本月销售额))

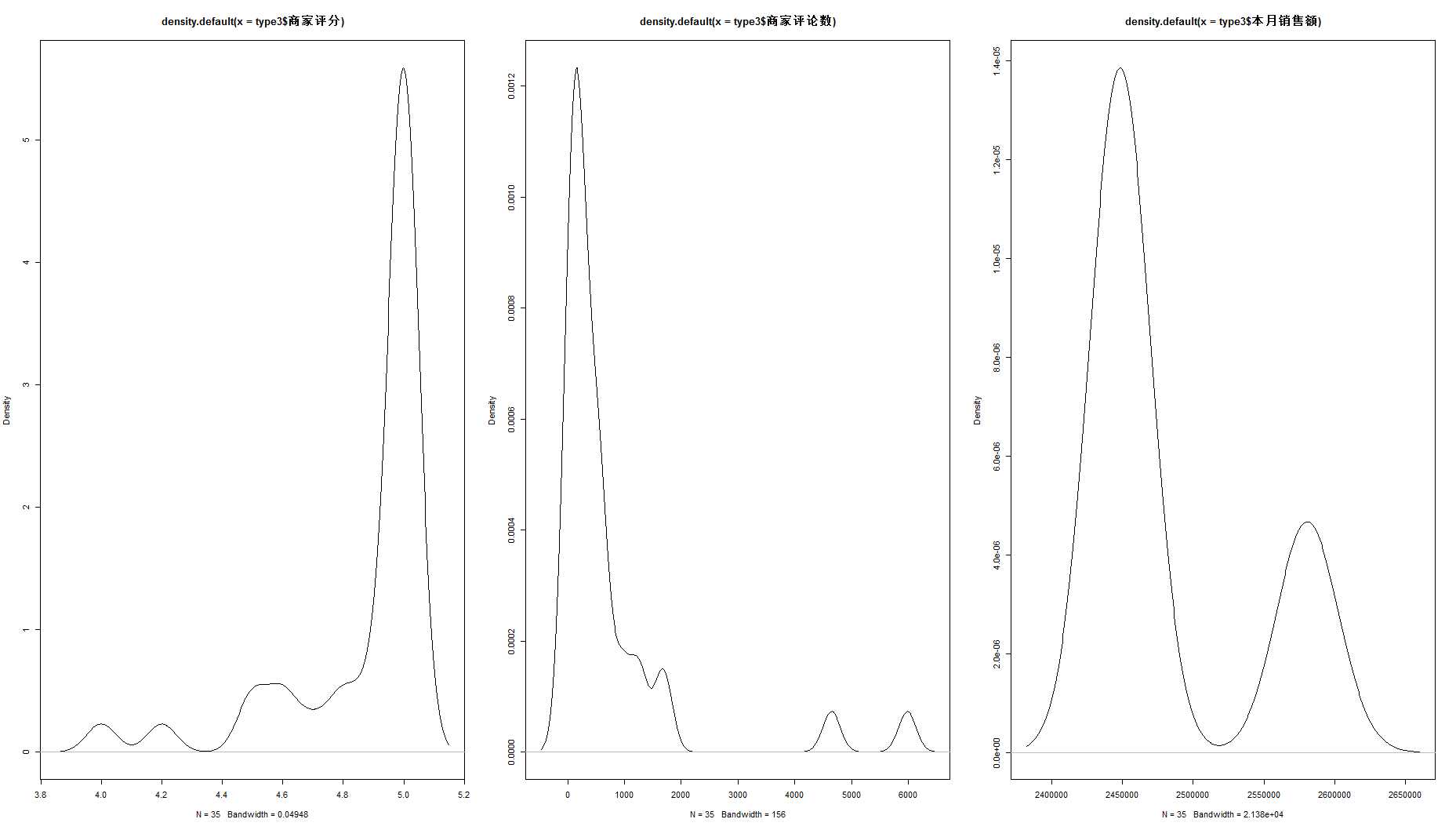
结合上述可视化结果，我们可以推断：type1代表评分较高但热度和知名度都较低的小店，这类店铺是我们推广宣传业务的最有潜力的客户群；type2代表评分较低且热度和知名度都较低的店，这类店在产品和宣传上都比较差劲，是比较劣质的客户群；type3代表着口碑和热度都较高的顶级店铺，这类店铺多为正新鸡排、一只酸奶牛这样的顶级连锁店铺，在宣传和产品上都很优秀，对我们推广宣传业务来说价值不大，因为已经有很成熟的广告体系。

以上便是此次简单的K-means聚类实战，如有不足望提出。