【BZOJ2721】[Violet 5]樱花 线性筛素数

【BZOJ2721】[Violet 5]樱花

Description

Input

Output

Sample Input

2

Sample Output

3

HINT

题解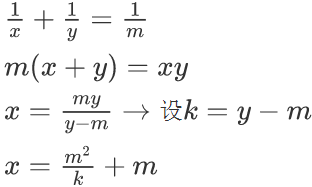：，所以就是求(n!)²的约数个数

又有一个结论，若n=Πpi^ei，那么n的约数个数就是Π(ei+1)，所以我们只需要筛出1-n 的所有素数，再分别计算每个素数的贡献就行了。

#include <cstdio>
#include <cstring>
#include <iostream>
#define mod 1000000007
using namespace std;
typedef long long ll;
const int maxn=1000010;
bool np[maxn];
int num;
int pri[maxn/10];
ll n,ans,sum;
int main()
{
	scanf("%lld",&n);
	ll i,j;
	for(i=2;i<=n;i++)
	{
		if(!np[i])	pri[++num]=i;
		for(j=1;j<=num&&i*pri[j]<=n;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)	break;
		}
	}
	ans=1,sum=0;
	for(i=1;i<=num;i++)
	{
		for(sum=0,j=pri[i];j<=n;j=j*pri[i])	sum=(sum+n/j)%mod;
		ans=ans*(2*sum+1)%mod;
	}
	printf("%lld",ans);
	return 0;
}