c语言实现队列的基本操作
话不多说,直接代码
- #include"stdio.h"
- #include"stdlib.h"
- typedef struct QNode{
- int date;
- struct QNode *next;
- }QNode,*QueuePtr;
- typedef struct{
- QueuePtr front;
- QueuePtr rear;
- }LinkQueue;
- //初始化
- int InitStack(LinkQueue &S){
- S.front=(QueuePtr)malloc(sizeof(QNode));
- //S.front=NULL;
- S.rear=S.front;
- if(!S.front)
- return ;
- S.front->next=NULL;
- return ;
- }
- //进
- int EnQueue(LinkQueue &S,int e){
- QueuePtr p=NULL;
- p=(QueuePtr)malloc(sizeof(QNode));
- if(!p)exit();
- p->date=e;
- p->next=;
- S.rear->next=p;
- S.rear=p;
- return ;
- }
- //置空
- void ClearQueue(LinkQueue &S){
- QueuePtr p=NULL;
- p=S.front;
- while(S.front!=S.rear){
- p=S.front->next;
- free(S.front);
- S.front=p;
- }
- }
- //判空
- void QueueEmpty(LinkQueue &S){
- if(S.front==S.rear)
- printf("判空:是\n");
- else
- printf("判空:否\n");
- }
- //长度
- int QueueLen(LinkQueue &S){
- QueuePtr p=NULL;
- int len=;
- p=S.front;
- if(S.front==S.rear)
- return len;
- else{
- while(p!=S.rear){
- len++;
- p=p->next;
- }
- return len;
- }
- }
- void len(LinkQueue &S){
- printf("%d\n",S.front);
- printf("%d\n",S.front->next);
- printf("%d\n",S.rear);
- printf("大小%d\n",sizeof(QNode));
- printf("%d\n",S.rear-S.front->next);
- printf("%d\n",S.rear-S.front);
- printf("%d\n",(S.rear-S.front->next)/sizeof(QNode));
- }
- //出
- int pop(LinkQueue &S){
- int tem=;
- QueuePtr p=NULL;
- if(S.front->next==NULL)
- return ;
- else{
- tem=S.front->next->date;
- p=S.front->next;
- free(S.front);
- S.front=p;
- return tem;
- }
- }
- //输出
- void QueueTraverse(LinkQueue &S){
- printf("输出:");
- QueuePtr p=S.front;
- while(p!=S.rear){
- printf("%d ",p->next->date);
- p=p->next;
- }
- }
- void main(){
- LinkQueue S;
- printf("初始化:");
- printf("%d\n",InitStack(S));
- printf("%d\n",EnQueue(S,));
- printf("%d\n",EnQueue(S,));
- printf("%d\n",EnQueue(S,));
- printf("%d\n",EnQueue(S,));
- printf("%d\n",EnQueue(S,));
- printf("长度:%d\n",QueueLen(S));
- len(S);
- QueueTraverse(S);
- printf("输出:%d\n",pop(S));
- QueueTraverse(S);
- EnQueue(S,);
- QueueTraverse(S);
- QueueEmpty(S);
- ClearQueue(S);
- QueueEmpty(S);
- }
在使用构造体的时候注意应该有两个构造体,分别对应整个链表和链表的一个结点。
在获取队列长度的时候不能像栈一样队首队尾直接相减,具体我也搞不懂为什么,代码中的len函数就是对该方法的测试。
另外,一定在。要注意S.front并不是第一个元素的位置,S.front->next才是,见图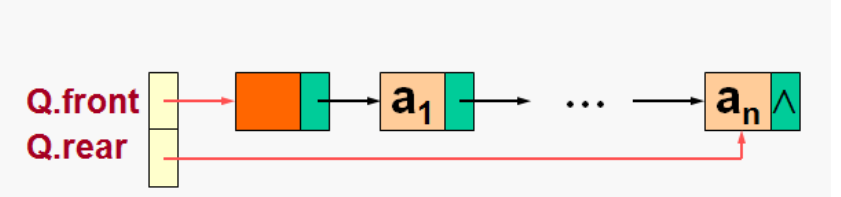
c语言实现队列的基本操作的更多相关文章
- 二、 编写一个类,用两个栈实现队列,支持队列的基本操作(add,poll,peek)
请指教交流! package com.it.hxs.c01; import java.util.Stack; /* 编写一个类,用两个栈实现队列,支持队列的基本操作(add,poll,peek) */ ...
- c语言描述的链队列的基本操作
#include<stdio.h> #include<stdlib.h> #define ok 0 #define error 1 //链队列特点在于不仅有链的头指针和尾指针, ...
- c语言多线程队列读写
最近用c语言写了个简单的队列服务,记录一下,文件结构为 main.c queue.c queue.h,代码如下: 主函数 #define NUM_THREADS 200 #include <st ...
- C语言实现二叉树的基本操作
二叉树是一种非常重要的数据结构.本文总结了二叉树的常见操作:二叉树的构建,查找,删除,二叉树的遍历(包括前序遍历.中序遍历.后序遍历.层次遍历),二叉搜索树的构造等. 1. 二叉树的构建 二叉树的基本 ...
- C语言数据结构-队列的实现-初始化、销毁、清空、长度、队列头元素、插入、删除、显示操作
1.数据结构-队列的实现-C语言 //队列的存储结构 #define MAXSIZE 100 typedef struct { int* base; //基地址 int _front; //头指针 i ...
- Go语言基础之16--Mysql基本操作
一.Mysql驱动及数据库连接 1.1 Golang中的Mysql驱动 A. https://github.com/go-sql-driver/mysql B. Go本身不提供具体数据库驱动,只提供驱 ...
- D_S 循环队列的基本操作
// main.cpp #include <iostream> using namespace std; #include "Status.h" typedef in ...
- C语言 复杂队列(链表队列)
//复杂的队列二 --链表队列 #include<stdio.h> #include<stdlib.h> #define datatype int struct queueli ...
- c语言对于文本的基本操作
字符读写函数 :fgetc和fputc 字符串读写函数:fgets和fputs 数据块读写函数:freed和fwrite 格式化读写函数:fscanf和fprinf 1.字符读写: fgetc函 ...
随机推荐
- 原生ajax访问服务器所展现的现象
<!DOCTYPE html><html><head><meta charset="UTF-8"><title>ajax ...
- Requests接口测试(三)
一.定制请求头 我们先来看一下,关于请求头的定制演示,相信了解http协议的小伙伴应该对请求头部headers请求头部并不陌生,那么作为实际工作中的我们,如果想自定义一些请求头的信息,我们应该怎么办呢 ...
- C++函数后面加throw关键字简记
看代码时候看到fun() throw()的用法,找到一篇blog解释很简单,如下: C++函数后面加关键字throw(something)限制,是对这个函数的异常安全性作出限制. 举例及解释如下: v ...
- 在Eclipse中连接SQL
原创 在Eclipse中连接SQL分为如下几个步骤: 1.加载驱动程序 2.创建连接对象 3.创建执行SQL语句的对象 4.执行SQL语句 5.关闭new出来的对象 1.加载驱动程序(以SQL为例) ...
- indexOf(String.indexOf 方法)
字符串的IndexOf()方法搜索在该字符串上是否出现了作为参数传递的字符串,如果找到字符串,则返回字符的起始位置 (0表示第一个字符,1表示第二个字符依此类推)如果说没有找到则返回 -1 返回 St ...
- delphi计算两个时间差
uses DateUtils; var S1, S2: string; T1, T2: TDateTime; D, H, M, S: Integer; Value: Int64; begin S1 : ...
- 【C#】浅克隆和深克隆的区别和在C#中的体现形式
前言:我们知道对象分引用类型和值类型. 浅克隆:复制一个现有对象,引用类型指向同一个内存块(string为最特殊的对象,这里当作值类型来看先) public class User { public i ...
- python 读取mysql存储的文件路径下载文件,内容解析,上传七牛云,内容入es
#!/usr/bin/env python # -*- coding: utf-8 -*- import ConfigParser import json import os import re fr ...
- LSI SAS3IRCU配置SAS3系列RAID卡
LSI SAS3IRCU配置SAS3系列RAID卡 一.适用的controller LSISAS3008 LSISAS3004 二.名词解释 Controller: IR: Volume: 卷,基于物 ...
- day3学python 字典+列表集合+文件读取
字典+列表集合+文件读取 字典示例 ************************ 各地食品的三级菜单************************* 1.使用字典嵌套字典 2.采用死循环思路 3 ...
