从XCodeGhost事件看软件来源鉴别的重要性

事件

事件引爆于9月18日乌云网公布的一则分析报告:“XCode编译器里有鬼 – XCodeGhost样本分析”，这份纯粹的技术分析报告引发中国iOS生态链的众多开发者的关注。 引起关注的人们对App Store上进行了筛查，结果令人震惊，至少有数十款流行的应用受到感染，其中包括了微信、网易云音乐、网易公开课、我叫MT、同花顺、南京银行、南方航空、中信银行行动卡空间、名片全能王、愤怒的小鸟2等等知名应用，被感染的用户估计超过1亿。

具体的说，这些APP使用了非苹果官方的，来自网盘等第三方下载平台，存在安全问题的Xcode开发环境。用这个XCode把应用源程序编译成可执行的APP时，APP会被自动添加病毒模块。用户从App Store下载安装这样的APP，手机就会中毒，病毒会偷偷地向作者的服务器上传软件包名、应用名、系统版本、语言、国家等信息。幸运的是，此次事件未给公众造成重大损失，还没用危及隐私或者帐号密码等敏感信息。然而，从技术层面看，这完全是病毒作者的“手下留情”，只要插入的病毒代码更恶毒一些，他就会获得超过1亿个“肉鸡”。

这一事件提示我们，使用数字签名或者散列（也称哈希Hash、摘要Digest）等加密机制，鉴别网上软件的来源是多么的重要。

散列值

散列函数（或散列算法，Hash Function）是从任何长度数据创建小的数字“指纹”的方法。散列将数据打乱混合计算，得到一个称为散列值的结果。散列值看起来通常是一个短的随机字母和数字组成的字符串。用作校验目的的散列函数是一个“单向”操作：对于给定的散列值，没有实用的方法可以计算出一个原始输入，也就是说很难伪造。被广泛使用的这类散列函数包括MD5，SHA-1，SHA-256等。许多软件在官网下载页面上提供了散列值。软件下载完成后，使用散列工具计算下载到的文件的散列值，与官网上的散列值（如图1所示）比对后即可确认所下载的软件与官网发布的是否完全一致。

图1  Ubuntu官网给出的安装光盘映像散列值

检验散列的工具和方法

虽然Windows系统内部广泛使用MD5、SHA1等常用散列算法，但是系统并没有提供一个计算MD5的程序或者命令。网络上有大量的计算散列的软件可供下载，可以在搜索引擎上搜索并参考口碑选择一个。使用openssl命令计算SHA1散列值的截图如下。

图 2 使用openssl命令计算散列值

Linux内置有md5sum, sha1sum这两个命令。在终端中运行md5sum <filename>，或者sha1sum <filename> 即可得到相应的散列值。

数字签名

数字签名就是附加在数据单元上的一些数据,或是对数据单元所作的密码变换。这种数据或变换允许数据单元的接收者用以确认数据单元的来源和数据单元的完整性并保护数据,防止被人(例如接收者)进行伪造。

数字签名（Digital Signature）技术是不对称加密算法的典型应用。数字签名的应用过程是，数据源发送方使用自己的私钥对数据校验和或其他与数据内容有关的变量进行加密处理，完成对数据的合法“签名”，数据接收方则利用对方的公钥来解读收到的“数字签名”，并将解读结果用于对数据完整性的检验，以确认签名的合法性。

数字签名的验证

Windows环境下，经过了数字签名的软件很容易验证其来源和洁净性。在文件属性对话框的“数字签名”页中，点击“详细信息”，即可检验软件的数字签名。下图是对从网盘上下载的android-studio-bundle-135.1740770-windows.exe的数字签名验证的结果。

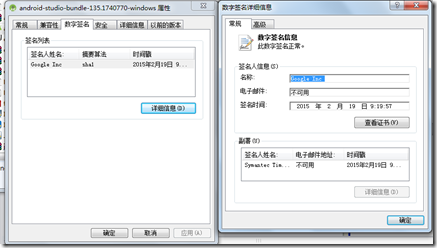
图2 有效的软件数字签名

如果软件被篡改，或者证书被篡改，都会导致签名的验证呈现无效的状态。下图是使用Hex编辑器人为修改Adobe Reader安装包之后，检测数字签名无效的截图。

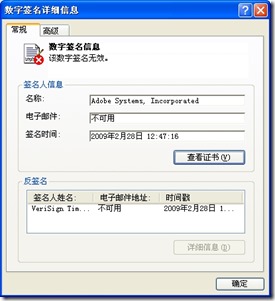
图3 无效的数字签名演示

小结

墙的存在，外部官网的可达性和速度是一个难以绕过得现实问题。墙内通过第三方下载平台获取Android Studio、XCode等开发工具，仍然将是很多人的首选。XCodeGhost事件提醒我们，从第三方渠道下载任何软件安装包之后，一定不要忽略检验数字签名，或者比对官网版本的散列值；无法通过验证的，必须果断拒之门外。其次，这一事件也与盗版的“黑苹果”有一定关系，“免费下载”的盗版软件决不是免费的！