GDOI2015的某道题目

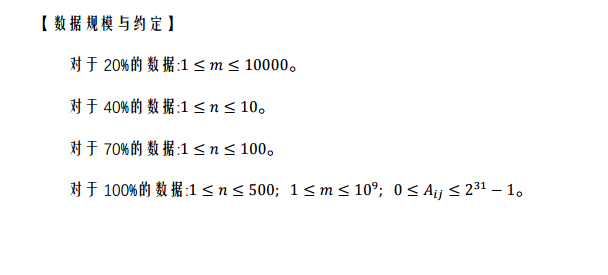
分析：

考试的时候由于一些神奇的原因(我就不说是什么了)...没有想$C$题，直接交了个暴力上去...

然后发现暴力的数组开的太大，由于矩阵乘法的需要做$m$次初始化，所以只拿到了10分...

我们一步一步来挖掘题目中隐含的条件...

首先，这个矩阵乘法很特殊，是位运算的形式，那么也就是说，每一位的运算是独立的，所以我们可以拆位，处理每一位的运算...

然后考虑对于其中的一位如何快速计算一个矩阵的$n$次幂...考虑到每一个格子只有可能是$0$或$1$，观察发现，对于数字$a[i][j]$，只有当第$i$行和第$j$列是相同的时候，我们新的到的矩阵中$a[i][j]$才是$0$，否则因为是$or$运算，所以只要有一位不同就是$1$...

那么我们考虑$A^{m-1}*A=A^{m}$，记$X=A^{m-1}$，$Y=A^m$，我们考虑$X$的每一个行向量对应的$Y$中的行向量是什么样子的，如果当前的行向量和$A$中的任意一个列向量都相等的话，那么新得到的行向量就是一个全为$1$的向量，否则，最多只有可能有$n$种取值，现在我们假设$A$中的每一个列向量都互不相同，那么也就是说，当前的行向量只有可能有一个地方是$0$，这个$0$最多有$n$中位置...所以当前行向量所对应的结果中的行向量最多有$n+1$种取值...因为每一次我们乘上的矩阵都是相同的，所以说无论进行多少次乘法，我们都只有可能在$n+1$种取值中给行向量赋值...那么也就是说，现在我们有一个$n+1$个点的图，然后我们需要在这张图上走$m-1$步，那么就可以倍增找到答案...至于对于图的预处理我们可以用$bitset$来加速...

没有想出来的原因：

没有充分利用到位运算的性质区进行拆位，没有想到去考虑每个行向量所对应的结果是存在循环的...

代码：

一开始实在不理解怎么做所以直接抄了一遍$std$...

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
//by NeighThorn
using namespace std;

const int maxn=500+5;

int n,m,tot,a[maxn][maxn],f[maxn<<1][30],id[maxn],ans[maxn][maxn];

struct M{

	unsigned long long a[8];

	friend bool operator == (M x,M y){
		for(int i=0;i<=7;i++)
			if(x.a[i]!=y.a[i])
				return false;
		return true;
	}

	inline void modify(int pos,int x){
		a[pos>>6]|=1ULL<<(pos&63);
		if(!x)
			a[pos>>6]^=1ULL<<(pos&63);
	}

	inline bool query(int pos){
		return (a[pos>>6]>>(pos&63))&1;
	}

}colu[maxn],node[maxn<<1];

inline int build(void){
	for(int i=1;i<=tot;i++)
		if(node[i]==node[tot+1])
			return i;
	int res=++tot;
	for(int i=1;i<=n;i++)
		node[tot+1].modify(i,!(node[res]==colu[i]));
	f[res][0]=build();
	return res;
}

signed main(void){
	freopen("C.in","r",stdin);
	freopen("C.out","w",stdout);
	scanf("%d%d",&n,&m);m--;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			scanf("%d",&a[i][j]);
	for(int i=0;i<=30;i++){
		for(int j=1;j<=n;j++)
			for(int k=1;k<=n;k++)
				colu[j].modify(k,(a[k][j]>>i)&1);
		tot=0;
		for(int j=1;j<=n;j++){
			for(int k=1;k<=n;k++)
				node[tot+1].modify(k,(a[j][k]>>i)&1);
			id[j]=build();
		}
		for(int j=1;j<=29;j++)
			for(int k=1;k<=tot;k++)
				f[k][j]=f[f[k][j-1]][j-1];
		for(int j=0;j<=29;j++)
			if(m&(1<<j))
				for(int k=1;k<=n;k++)
					id[k]=f[id[k]][j];
		for(int j=1;j<=n;j++)
			for(int k=1;k<=n;k++)
				ans[j][k]|=node[id[j]].query(k)<<i;
	}
	for(int i=1;i<=n;i++,puts(""))
		for(int j=1;j<=n;j++)
			printf("%d ",ans[i][j]);
	return 0;
}
/*
Never give up.
Bless all.
*/

　　

---

By NeighThorn