【Calculus 微积分の一些个人理解】

微积分

微积分（Calculus）是高等数学中研究函数的微分（Differentiation）、积分(Integration)以及有关概念和应用的数学分支.它是数学的一个基础学科.内容主要包括极限、微分学、积分学及其应用.微分学包括求导数的运算,是一套关于变化率的理论.它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论.积分学,包括求积分的运算,为定义和计算面积、体积等提供一套通用的方法.

微积分包括微分和积分,积分和微分互为逆运算,积分又包括定积分和不定积分,定积分是变量限定在一定的范围内的积分,不定积分是没范围的.

众所周知,微积分的两大部分是微分与积分.一元函数情况下,求微分实际上是求一个已知函数的导函数,而求积分是求已知导函数的原函数.所以,微分与积分互为逆运算.

微分是对原函数求其导函数,积分则是由导函数求其原函数.

定积分是一个面积,而不定积分是表达式.

是牛顿和莱布尼茨创造性的将两者联系在了一起.即微积分基本定理.

补充：

积分中定积分与不定积分与变限积分的区别和联系：

（1）不定积分：

设f(x)定义在某区间I上，若存在可导函数F(x)，使得F'(x)=f(x)对任意x属于I都成立，那么则称F(x)是f(x)在区间I上的一个原函数。
我们把这个全体原函数，也称为不定积分。因此，不定积分的定义是找原函数的，即得到。

（2）定积分:

如果大家翻下课本的话，会记得定积分的定义是根据求曲边梯形的面积得出来的。因此，定积分的定义是用来求面积的，即得到一个数。
引用百度百科的解释，看看图片：

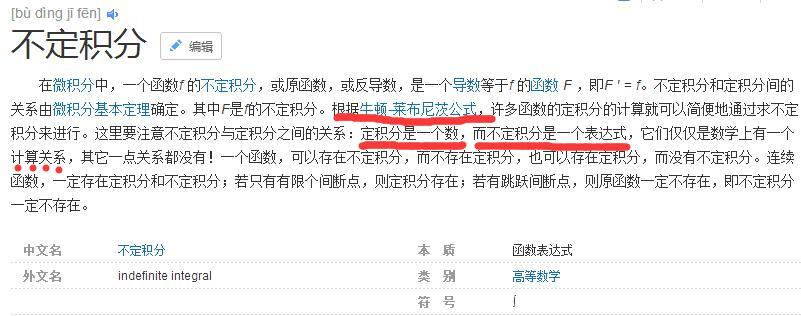
一个是函数，一个是数值，这肯定不一样呀！

为什么会产生这样的误区？

有人就会问了：不是有个牛顿莱布尼茨公式吗？--------这就是大多数初学者在学习这块时容易犯的概念错误。
牛顿莱布尼茨公式是在不定积分和定积分的概念出来后，创造性地把他们通过一个式子联立起来了，也就是说，定积分的面积，是可以通过寻找到它的原函数，再代入上下限而求得，这与用定积分的定义去计算是一样可以算出正确结果的，而且这个方法会更快！换句话说：牛顿莱布尼茨公式只是一个计算工具，但不是定义！
只有先从概念上理解了不定积分和定积分的区别，接下来的变限积分和反常积分就很容易理解了。

（3）变限积分：

先想想变限积分属于哪一类范畴？它是将定积分的上下限换成了变量x，也就是说你那个曲边梯形的面积是随着x的滑动变化而变化的。取不同的x，就有不同的面积效果，x 在几何上是一个动的边。因此，变限积分仍然属于定积分的范畴，即是求面积的。那么，变限积分和不定积分、定积分的关系又是什么呢？请看下图：

补充：

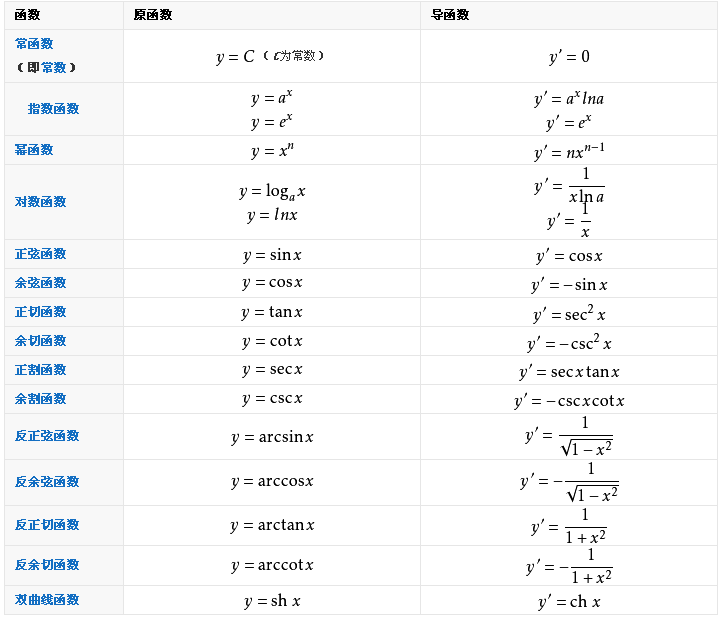
导数(某点的导数即在导函数上的值就是在原函数上的斜率就是k值就是tan a)：

导数（Derivative）是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'(x0)或df(x0)/dx。

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。
不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。然而，可导的函数一定连续；不连续的函数一定不可导。

对于可导的函数f(x)，x↦f'(x)也是一个函数，称作f(x)的导函数（简称导数）。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上，求导就是一个求极限的过程，导数的四则运算法则也来源于极限的四则运算法则。反之，已知导函数也可以倒过来求原来的函数，即不定积分。微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作，它们都是微积分学中最为基础的概念。