matlab学习笔记之求解线性规划问题和二次型问题

一、线性规划问题

　　已知目标函数和约束条件均为线性函数，求目标函数的最小值（最优值）问题。

1.求解方式：用linprog函数求解

2.linprog函数使用形式：

　　x=linprog(f,A,b) 

　　x=linprog(f,A,b,Aeq,beq) 

　　x=linprog(f,A,b,Aeq,beq,lb,ub) 

　　x=linprog(f,A,b,Aeq,beq,lb,ub,x0) 

　　x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options)  

　　[x,fval]=linprog(…) 

　　[x, fval, exitflag]=linprog(…) 

　　[x, fval, exitflag, output]=linprog(…) 

　　[x, fval, exitflag, output, lambda]=linprog(…)

3.介绍一种最常用的：

　　[x,fval,exitflag,output,lambda] = linprog(f,A,b,Aep,beq,lb,ub); 

其中，f是目标函数系数矩阵；A和b是不等式约束条件的参数；Aeq和beq是等式约束条件的参数；lb和ub为x取值的取值范围。

　　lambda.ineqlin—不等式约束A,b

　　lambda.eqlin—等式约束Aep,bep

　　lambda.upper—上界条件ub

　　lambda.lower—下界条件lb

4.实例：

目标函数：f(x) = –5x1 – 4x2 –6x3,

约束条件：

　　x1 – x2 + x3 ≤ 20

　　3x1 + 2x2 + 4x3 ≤ 42

　　3x1 + 2x2 ≤ 30

　　0 ≤ x1, 0 ≤ x2, 0 ≤ x3

Matlab程序：

>> f = [-; -; -]; A = [ - ;   ;   ]; b = [; ; ]; lb = zeros(,);
>> [x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb);
>> x
x =
    0.0000
   15.0000
    3.0000

>> fval
fval =
  -78.0000

二、二次型规划问题

　　理解完线性规划问题再来学习二次型规划问题就简单得多了，可以相似类比。

1.求解方式：用quadprog函数来求解

2.quadprog函数使用形式：

　　x = quadprog(H,f)

　　x = quadprog(H,f,A,b)

　　x = quadprog(H,f,A,b,Aeq,beq)

　　x = quadprog(H,f,A,b,Aeq,beq,lb,ub)

　　x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)

　　x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)

　　x = quadprog(problem)

　　[x,fval] = quadprog(H,f,...)

　　[x,fval,exitflag] = quadprog(H,f,...)

　　[x,fval,exitflag,output] = quadprog(H,f,...)

　　[x,fval,exitflag,output,lambda] = quadprog(H,f,...)

 

3.实例：

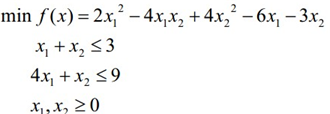
Matlab程序：

>> H = [ -;- ];f = [-;-];A = [ ; ];b = [;];lb = ones(,);
>> [x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb);
>> x
x =
    1.9500

    1.0500

>> fval
fval =
  -11.0250

注：若求解的是最大值问题亦可转化为求最优化问题。