Coderforces 85 D. Sum of Medians（线段树单点修改）

D. Sum of Medians

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

In one well-known algorithm of finding the k-th order statistics we should divide all elements into groups of five consecutive elements and find the median of each five. A median is called the middle element of a sorted array (it's the third largest element for a group of five). To increase the algorithm's performance speed on a modern video card, you should be able to find a sum of medians in each five of the array.

A sum of medians of a sorted k-element set S = {a₁, a₂, ..., a_k}, where a₁ < a₂ < a₃ < ... < a_k, will be understood by as

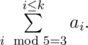
The 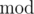operator stands for taking the remainder, that is 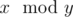stands for the remainder of dividing x by y.

To organize exercise testing quickly calculating the sum of medians for a changing set was needed.

Input

The first line contains number n (1 ≤ n ≤ 10⁵), the number of operations performed.

Then each of n lines contains the description of one of the three operations:

• add x — add the element x to the set;
• del x — delete the element x from the set;
• sum — find the sum of medians of the set.

For any add x operation it is true that the element x is not included in the set directly before the operation.

For any del x operation it is true that the element x is included in the set directly before the operation.

All the numbers in the input are positive integers, not exceeding 10⁹.

Output

For each operation sum print on the single line the sum of medians of the current set. If the set is empty, print 0.

Please, do not use the %lld specificator to read or write 64-bit integers in C++. It is preferred to use the cin, cout streams (also you may use the %I64d specificator).

Examples

Input

6
add 4
add 5
add 1
add 2
add 3
sum

Output

3

Input

14
add 1
add 7
add 2
add 5
sum
add 6
add 8
add 9
add 3
add 4
add 10
sum
del 1
sum

Output

5
11
13
【分析】有n个操作，1：向集合中加一个数x；2：去掉集合中的数x；3：询问从小到大排序后，所有下标i%5==3的值的和。
刚开始想到线段树了，但是不知道怎么写，然后看了网上的题解。。。好强啊！！！每个节点额外保存此区间i=0~4的和，然后cnt数组保存此区间 元素的个数。
然后求和合并的时候，sum[rt][i]=sum[rt*2][i]+sum[rt*2+1][(i-cnt[rt*2]%5+5)%5];这个公式可以自己推一下。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <time.h>
#include <string>
#include <map>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#define met(a,b) memset(a,b,sizeof a)
#define pb push_back
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
using namespace std;
typedef long long ll;
const int N=2e5+;
const int M=N*N+;
int num,s,m,n,q;
int a[N],op[N],b[N];
ll sum[N*][];
int cnt[N*];
inline void PushPlus(int rt) {
    cnt[rt]=cnt[rt*]+cnt[rt*+];
    for(int i=;i<=;i++){
        sum[rt][i]=sum[rt*][i]+sum[rt*+][(i-cnt[rt*]%+)%];
    }
}

void Update(int p,int add,int l,int r,int rt,int x) {
    if(l==r) {
        sum[rt][]+=add;
        cnt[rt]+=x;
        return;
    }
    int m=(r+l)>>;
    if(p<=m)Update(p,add,lson,x);
    else Update(p,add,rson,x);
    PushPlus(rt);
}

int main() {
    int u,vv,w;
    scanf("%d",&q);
    char str[];
    n=;
    for(int i=;i<=q;i++){
        scanf("%s",str);
        if(str[]=='a'){
            scanf("%d",&b[i]);
            op[i]=;
            a[++n]=b[i];
        }
        else if(str[]=='d'){
            scanf("%d",&b[i]);
            op[i]=-;
        }
        else {
            op[i]=;
        }
    }
    sort(a+,a+n+);
    n=unique(a+,a+n+)-a-;
    for(int i=;i<=q;i++){
        if(abs(op[i])==){
            int p=lower_bound(a+,a++n,b[i])-a;
            Update(p,b[i]*op[i],,n,,op[i]);
        }
        else {
            printf("%lld\n",sum[][]);
        }
    }
    return ;
}