雷神领域（并查集真是个好东西）并查集+流氓dp

考场上，整整看了半个小时以上的题目！！！

化简题意：

给定一个全0矩阵，一些坐标点（x，y）为1，当三个点可以构成一个直角三角形时（直角边长为整数）拓展为一个矩形，之后从（0，0）出发，求最多的占用行数或占用列数

反正就是很麻烦的题就对了。。。

考场历程：

1、没看懂题，就去看下一题了

2、第三题可做性极差（tpsort+dp或网络流）

3、n^2拓展完了新点，发现样例就是个弟弟！（拓展完变成全1矩阵）

4、最小最大，想着二分来着，但是秒pass

5、想强行建边，跑最短路

6、dp根本想不出来....（行和列）

7、考完之后发现这题就是在侮辱智商

solution：

首先，n^2拓展点很容易，枚举点如何暴力即可。

先来讲dp怎么写吧.....

这个dp就是流氓.....

怎么说呢，考场上一直在想：跑一个行最优，列最优，比最小值，就成了最长不下降子序列之类的东西...

但是路径不一定是一个嘢....

于是考场就暴毙了

其实，dp方程式....

• 二维，f[i][j]表示从（0,0）拓展到当前点的最大值
• 如果当前点是1点，+1
• 如果不是，就更新，从左边和上边找一个最大值续上
• 我管你是行最大还是列最大，都给我最大然后+1再说

这就是这个dp欠的地方（还是我太弱了）

dp的事解决了，加上之前的n^2拓展点，理论上5000*5000应该是能过去的，但是25000000，加上3~4的常数，确实是会T掉1~2个点。

于是，这里有一个结论（我考场上也发现了呃呃呃）如果是对应坐标的三个点可以拓展另外一个点，那么，这三个点的坐标一定对应了四个数（两个数对）

两个数对自由组合，就成了4个点，而我们已知了三个点，只需要在查询的时候查询一下是否出现过四个数就行了。

有点难以理解....借图

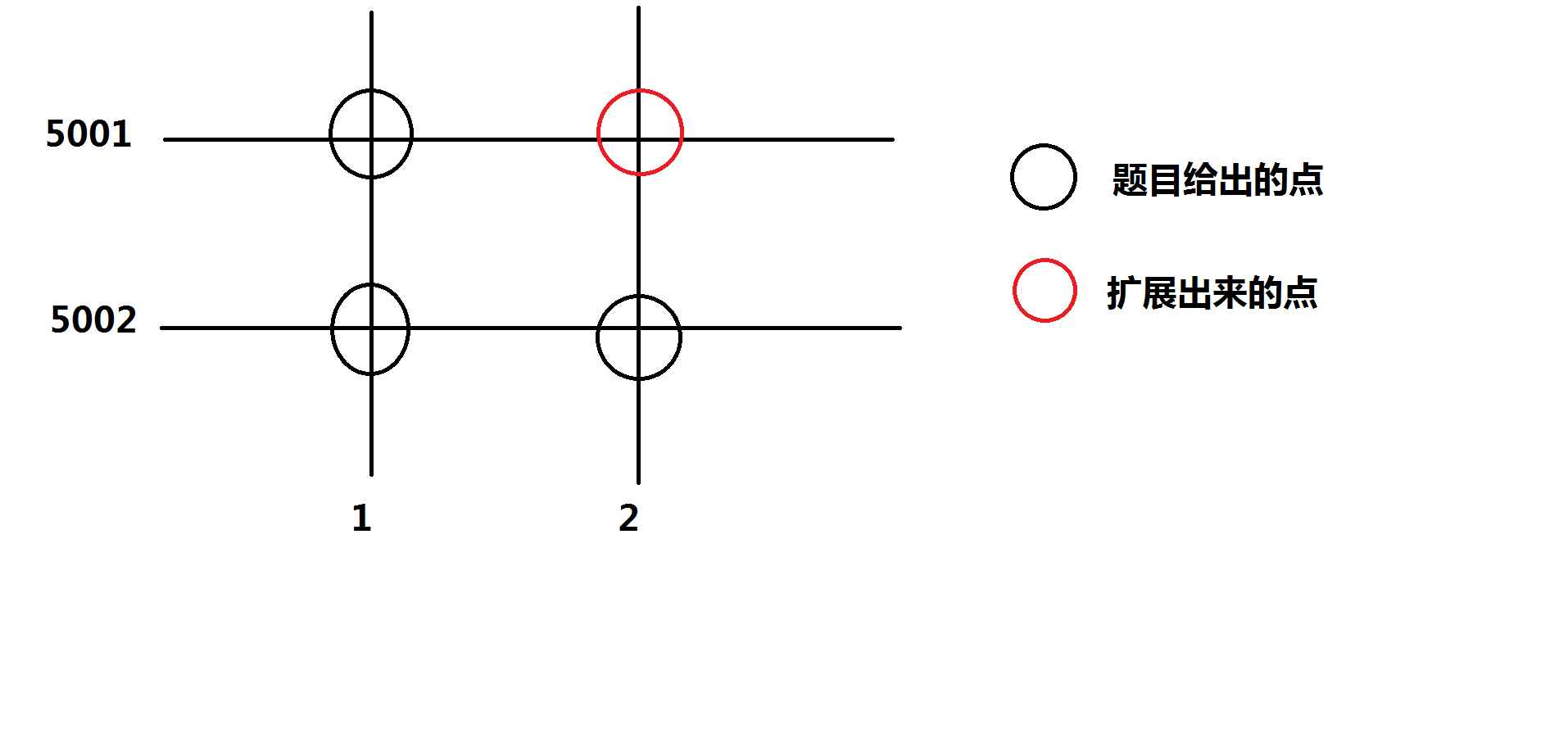
给出的三个点的坐标为（1,5001）（1,5002），（2,5002），我们把横坐标放在一个集合，纵坐标放在一个集合{1,2}{5001,5002}，自由组合，就能够快速地判断是否存在这个点了。

因为是两个集合，所以并查集数组要开两倍

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=;
int n;
int fa[maxn*+];
inline int find(int x)
{return fa[x]==x?x:fa[x]=find(fa[x]);}
int f[maxn+][maxn+]; 

int main()
{
    scanf("%d",&n);
    for(int i=;i<=;i++)
    fa[i]=i;
    for(int i=;i<=n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        fa[find(x)]=find(y+maxn);
    }
    for(int i=;i<=maxn;i++)
    {
        for(int j=;j<=maxn;j++)
        {
            if(find(i)==find(j+maxn))
            {
                f[i][j]=f[i-][j-]+;
            }
            else
            f[i][j]=max(f[i][j-],f[i-][j]);
        }
    }
    printf("%d",f[maxn][maxn]);
    return ;
}

（完）