【数据结构】什么是AVL树

什么是AVL树

目录

• 什么是AVL树
  • 1. 什么是AVL树
  • 2. 节点的实现
  • 3. AVL树的调整
    • 3.1 LL旋转
    • 3.2 RR旋转
    • 3.3 RL旋转
    • 3.4 LR旋转

---

二叉查找树的一个局限性就是有可能退化成一个链表，这种情况下二叉查找树的效率就会急剧下降变成0(n)。而AVL树可以很好地解决BST的这种困境。本篇博客会介绍AVL树的基本特点和相关操作。

文章参考自博客：二叉树-你可能需要知道的知识点

---

1. 什么是AVL树

任何两个子树的高度差最大是1，这样的二叉树叫做AVL树。

先来确定几个概念：

平衡因子：将二叉树上节点的左子树高度减去右子树高度的值称为该节点的平衡因子BF(Balance Factor)。

最小不平衡子树：距离插入节点最近的，且平衡因子的绝对值大于1的节点为根的子树。

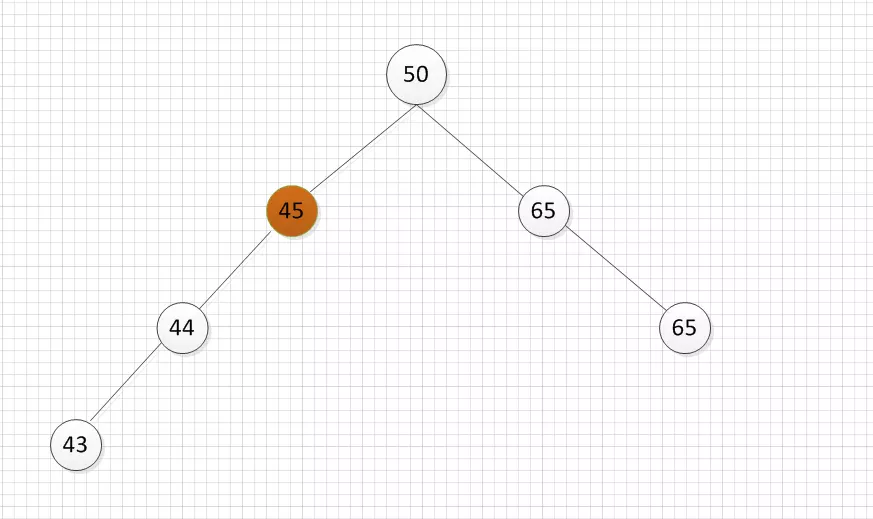
左边二叉树的节点45的BF = 1，插入节点43后，节点45的BF=2。

节点45是距离插入点43最近的BF不在[-1,1]范围内的节点，因此以节点45为根的子树为最小不平衡子树。

2. 节点的实现

public class AVLTreeNode<T extends Comparable> {

    // 存储的数据-用于排序
    T key;

    // 节点高度-用于计算父节点的BF
    int height;

    // 左儿子 & 右儿子
    AVLTreeNode<T> left;
    AVLTreeNode<T> right;

    public AVLTreeNode() {
    }

    public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) {
        this.key = key;
        this.left = left;
        this.right = right;
        this.height = 0;
    }

}

节点的定义还是比较简单的，相对于之前的定义多了一个height属性用于计算父节点的BF。

树的定义

public class AVLTree<T extends Comparable> {
    // 定义树的根节点
    AVLTreeNode<T> root;

    public AVLTree() {
        root = null;
    }
}

获取树的高度

    public int height() {
        return height(root);
    }

    private int height(AVLTreeNode<T> tree) {
        if (tree != null){
            return tree.height;
        }
        return 0;
    }

本文章将空树的高度定义为0，高度以树的层次为准，根节点的高度为1，依次类推。

3. AVL树的调整

如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。这种不平衡可能出现在下面四种情况中：

• 对a的左儿子的左子树进行一次插入。（LL）
• 对a的左儿子的右子树进行一次插入。（LR）
• 对a的右儿子的左子树进行一次插入。（RL）
• 对a的右儿子的右子树进行一次插入。（RR）
  
  其中1、4是关于a点的镜像对称，2、3是关于a点的镜像对称。

第一种情况（1、4）需要通过对树的一次单旋转完成调整。

第二种情况（2、3）需要通过对树的一次双旋转完成调整。

3.1 LL旋转

在左子树上插入左孩子导致AVL树失衡,"根的左子树的高度"比"根的右子树的高度"大2。针对该情况，我们需要进行单右旋转来完成对树的调整。

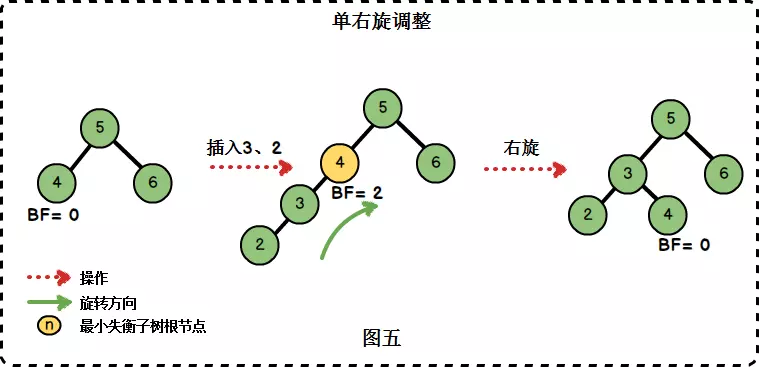
图中左边是旋转之前的树，右边是旋转之后的树。从中可以发现，旋转之后的树又变成了AVL树，而且该旋转只需要一次即可完成。

对于LL旋转，你可以这样理解为：LL旋转是围绕"失去平衡的AVL根节点"进行的，也就是节点4；而且由于是LL情况，就将节点4进行一次顺时针旋转。

代码实现：

    /**
     * 进行一次单右旋转
     *
     * @param node 最小失衡树根节点
     */
    private AVLTreeNode<T> rightRotation(AVLTreeNode<T> node) {
        AVLTreeNode<T> left = node.left;
        node.left = left.right;
        left.right = node;
        // 更新高度
        node.height = Math.max(height(node.left), height(node.right)) + 1;
        left.height = Math.max(height(left.left), height(left.right)) + 1;
        return left;
    }

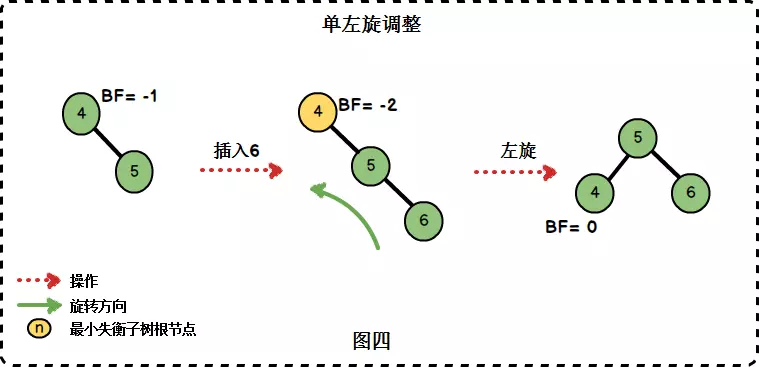
3.2 RR旋转

在右子树插入右孩子导致AVL失衡时，我们需要进行单左旋调整。旋转围绕最小失衡子树的根节点进行。

    /**
     * 进行一次单左旋转
     *
     * @param node 最小失衡树根节点
     */
    private AVLTreeNode<T> leftRotation(AVLTreeNode<T> node) {
        AVLTreeNode<T> right = node.right;
        node.right = right.left;
        right.left = node;

        // 更新高度
        node.height = Math.max(height(node.left), height(node.right)) + 1;
        right.height = Math.max(height(right.left), height(right.right)) + 1;

        return right;

    }

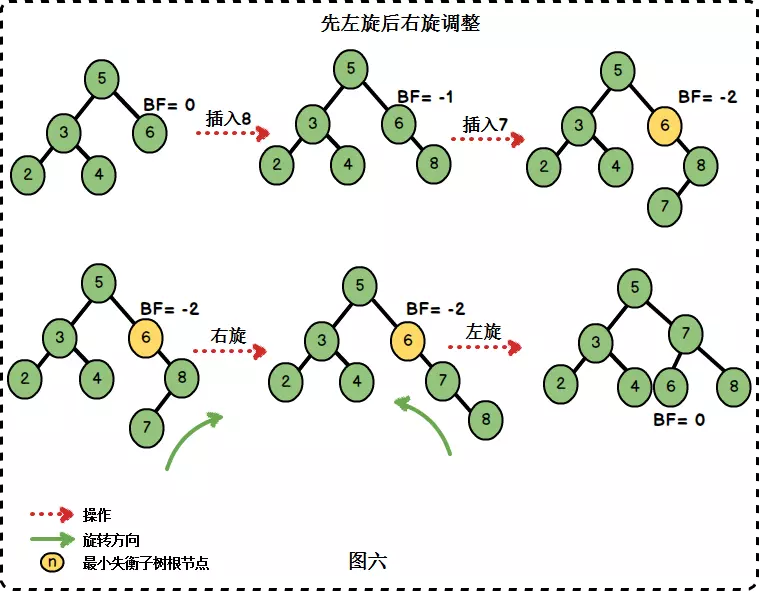
3.3 RL旋转

“在右子树上插入左孩子导致AVL树失衡",此时我们需要进行先右旋后左旋的调整。

    /**
     * 先右旋后左旋
     *
     * @param node 失衡树根节点
     * @return 旋转后的根节点
     */
    private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> node) {
        node.right = rightRoation(node.right);

        return leftRoation(node);

    }

3.4 LR旋转

“在左子树上插入右孩子导致AVL树失衡",此时我们需要进行先左旋后右旋的调整。

    /**
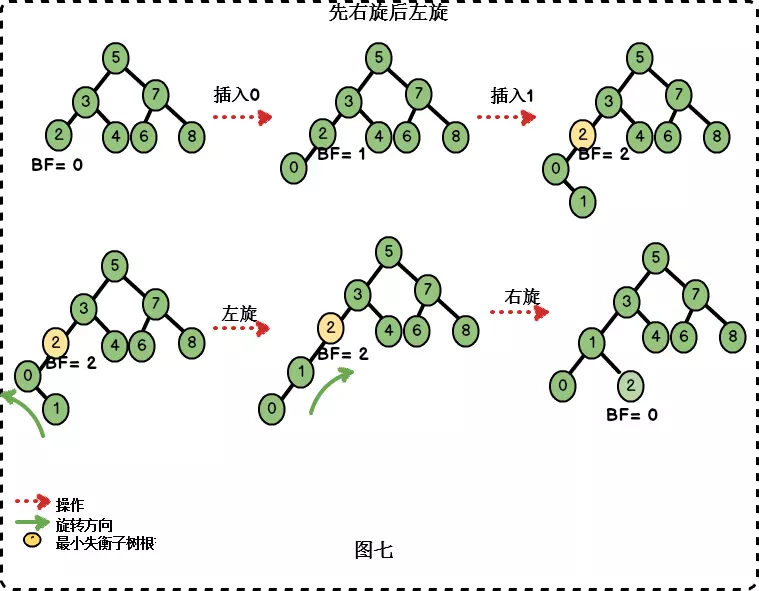
     * 先左旋后右旋
     *
     * @param node 失衡树根节点
     * @return 旋转后的根节点
     */
    private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> node) {
        node.left = leftRoation(node.left);

        return rightLeftRoation(node);

    }